Дальнейшим развитием схемы программной системы с блоком восстановления стало применение мультиверсионного программирования альтернатив. При таком подходе каждая альтернатива представляет собой набор функционально эквивалентных версий, исполнение которых происходит одновременно и параллельно, а результаты оцениваются с помощью алгоритмов голосования [4]. Подобная реализация программных систем получила название блока восстановления с согласованием [5].
Основной проблемой избыточной реализации программных систем является потребность в дополнительных ресурсах. Это приводит к необходимости решения задачи максимизации надежности программной системы с учетом существующих ограничений на стоимость, время реализации, использования компонент собственной разработки и приобретенных программных компонент. Подробно данная задача описана в [2].
Довольно часто при решении практических задач исходная информация является неполной или неточной [3, 8]. Существующие исследования в отношении надежности программных систем показывают, что не все параметры задачи четко заданы. Различные цели и ограничения, задаваемые проектировщиком программных систем, а также показатели затрат, включаемые в функцию стоимости, определяются на основании предыдущего опыта и информации, доступной из различных баз данных [10]. В связи с этим проектировщику сложно задать точные значения возможных финансовых затрат и использования различных ресурсов [6]. Более того, сложность проекта, новизна задачи, возможные изменения требований заказчика, а также ряд факторов, которые неизвестны на начальном этапе проекта, но могут появиться позже, увеличивают степень неточности и неопределенности. Кроме этого, требуемые значения могут быть преднамеренно заданы нечетко, чтобы обеспечить определенный уровень допустимого отклонения по этим параметрам [7].
Все это приводит к формализации задачи как нечеткой, и для ее решения целесообразным становится использование методов нечеткой оптимизации, которые позволяют найти решение задачи в условиях неопределенности [1].
В данной статье рассматривается задача оптимизации состава программной системы по схеме блока восстановления с согласованием, для решения которой предложен алгоритм работы метода нечеткой оптимизации. Предлагаемый алгоритм позволяет сформировать программную систему, отличающуюся высоким уровнем надежности и минимальными затратами на ее реализацию.
Задача оптимизации состава программной системы
Задача формирования программной системы по схеме блока восстановления с согласованием может быть рассмотрена как двуцелевая задача оптимизации: макимизировать надежность программной системы и одновременно с этим минимизировать ее стоимость. Формально данную задачу можно записать следующим образом:
![]()
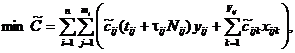 (1)
(1)
где знак тильды (~) над коэффициентами целевых функций означает, что они являются нечеткими числами.
Условные обозначения:
R – надежность (вероятность безотказной работы) программной системы;
Ri – надежность i-го модуля программной системы;
C – стоимость программной системы;
cij – стоимость j-й альтернативы i-го модуля;
cijk – стоимость k-й версии j-й альтернативы i-го модуля;
n – количество модулей в программной системе;
mi – количество альтернатив, доступных для i-го модуля;
Vij – количество версий, доступных для j-й альтернативы i-го модуля;
L – количество функций, которые выполняет программная система;
fl – частота использования функции l;
sl – множество модулей, необходимых для выполнения функции l;
xijk – булева переменная, равная 1, если выбранная k-я версия j-й альтернативы i-го модуля создана сторонними разработчиками, 0 – если версия разработана самостоятельно;
yij – булева переменная, равная 1, если j-я альтернатива i-го модуля разрабатывается собственными силами, 0 – в противном случае;
tij – расчетное время разработки j-й альтернативы i-го модуля;
τij – среднее время тестирования j-й альтернативы i-го модуля;
Nij – общее количество тестовых испытаний.
Надежность модуля программной системы, создаваемой согласно схеме блока восстановления с согласованием, вычисляется следующим образом:
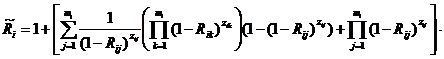
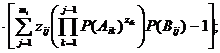
![]()
![]()
![]()
где Rij – надежность j-й альтернативы i-го модуля; zij – булева переменная, равная 1, если j-я альтернатива присутствует в i-м модуле, 0 – в противном случае; Aij – событие, соответствующее отклонению результата j-й альтернативы i-го модуля; Bij – событие, соответствующее принятию корректного результата j-й альтернативы i-го модуля; p1 – вероятность того, что следующая альтернатива не будет вызвана, несмотря на отказ текущей альтернативы; p2 – вероятность неверной оценки корректного результата; p3 – вероятность принятия неверного результата за корректный.
Алгоритм формирования оптимального состава программной системы
Следующий алгоритм описывает последовательность шагов решения задачи формирования оптимального состава программной системы, создаваемой согласно схеме блока восстановления с согласованием, как задачи нечеткого математического программирования.
Шаг 1. Вычисление четких эквивалентов нечетких параметров с помощью функции дефаззификации. Отметим, что для каждого из параметров используется одна и та же функция дефаззификации.
Будем использовать следующую функцию дефаззификации:
![]()
где al, am, au – являются треугольными нечеткими числами.
Шаг 2. Включение целевой функции минимального (максимального) оператора в виде нечеткого ограничения. Тогда задачу формирования оптимального состава избыточного программного обеспечения можно представить как
![]()
при условиях:
![]()
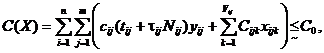
![]()
где R0 и C0 – дефаззифициорованные уровни желаемой надежности и стоимости.
Шаг 3. Определение соответствующих функций принадлежности для каждого нечеткого неравенств:
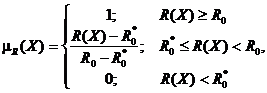
где R0 – желаемый уровень, а R0* – уровень допустимого отклонения к нечеткому ограничению целевой функции надежности.
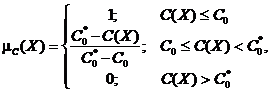
где С0 – ограничение и C0* – уровень допустимого отклонения от нечеткого ограничения по бюджету.
Шаг 4. Чтобы найти нечеткое решение, используем принцип расширения, что приводит к задаче четкого математического программирования, выраженной как
![]()
при условиях:
![]()
![]()
![]()
где α отражает степень достижения уровня, заданного лицом, принимающим решение (ЛПР).
Шаг 5. При решении задачи на шагах алгоритма 1–4 целевая функция рассматривается как ограничение. Каждое ограничение рассматривается как цель для ЛПР, а задача может быть представлена как задача нечеткого многокритериального математического программирования. Помимо этого, каждая цель может обладать различным уровнем важности, ей может присваиваться определенный весовой коэффициент, выражающий ее относительную значимость. Полученную задачу можно решить при помощи взвешенного минимаксного подхода. Четкая формулировка взвешенной задачи задается как
![]() (2)
(2)
при условиях:
![]()
![]()
![]()
![]()
![]()
Данная задача может быть решена с помощью стандартных подходов математического программирования.
Шаг 6. При подстановке значений для μR(x) и μC(x) задача принимает вид:
![]() (3)
(3)
при условиях:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Шаг 7. В случае, если допустимое решение задачи (2) или (3) не получено, можно использовать метод нечеткого целевого программирования для получения компромиссного решения, например, предложный Мохамедом в [9].
Так, если задача (3) нерешаема, т.е. цель не может быть достигнута для допустимого значения α ∈ [0, 1], то можно использовать следующий метод нечеткого целевого программирования для получения компромиссного решения. Максимальное значение, которое может принимать функция принадлежности, равно единице. Максимизация α ∈ [0, 1] равнозначна задаче максимального приближения его значения к 1. Этого можно добиться путем минимизации отрицательных переменных целевого программирования (т.е. η), отклоняющихся от единицы. Формулировка задачи (3) в рамках нечеткого программирования с введением отрицательных и положительных переменных отклонения ηj и ρj может быть задана следующим образом:
![]() (4)
(4)
при условиях:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом, решение задачи (1) может быть получено путем решения задачи (4).
Заключение
Оптимизация состава избыточных программных систем всегда является нетривиальной проблемой, требующей учета ряда параметров системы и специфики самой задачи. В данной статье предложен алгоритм, предназначенный для формирования оптимального состава программной системы схемы блока восстановления с согласованием. Решение данной задачи в условиях неопределенности, связанной с неточностью и неполнотой информации о ряде характеристик программной системы, стало возможным при использовании математического аппарата нечеткой логики. Предложенный в статье алгоритм нечеткой оптимизации позволяет сформировать программную систему с блоком восстановления с согласованием, обеспечивая высокий уровень надежности системы с минимальными затратами на ее создание. Данный алгоритм может быть использован для формирования программных систем, применяемых в критичных по надежности реализации их целевых функций областях.
Рецензенты:Бронов С.А., д.т.н., профессор, руководитель научно-учебной лаборатории систем автоматизированного проектирования кафедры систем искусственного интеллекта Сибирского федерального университета, г. Красноярск;
Носков М.В., д.ф.-м.н., профессор, заместитель директора по научной работе Института космических и информационных технологий Сибирского федерального университета, г. Красноярск.



