Успешность формирования универсальных учебных действий (УУД), которые являются надпредметными умениями, существенно зависит от того, насколько органично они встроены в предметное обучение. Но сегодня такое встраивание, будучи вполне конструктивно описанным для начальной школы [6], для основного общего образования пока присутствует в основном как декларация. В то же время в ряде публикаций (см. [3] и [7]) показано, что изучение математики на ступени основного общего образования предоставляет широкие возможности для развития целого спектра УУД различных групп. Однако, в отличие от многих предметов естественно-научного цикла, где для развития УУД активно используется компьютерная визуализация, в преподавании математики весьма слабо освещены такие аспекты применения информационно-коммуникационных технологий, в том числе интерактивных геометрических сред (ИГС), именно с точки зрения формирования и развития УУД.
Опыт использования ИГС в преподавании геометрии, описанный в наших работах [1] и [5], показывает, что возникает возможность так формулировать задание учащимся, чтобы ответ в нем был получен из опыта планируемой деятельности по получению необходимой информации. В такой ситуации происходит развитие регулятивных УУД, формирование которых было начато в начальной школе, ибо в таком задании учащимся нужно провести целеполагание на основе соотнесения того, что уже им было известно, и того, какой информации им недостает, планирование последовательности действий для получения недостающей информации, прогнозирование результата и т.д. Развиваются познавательные УУД – как общеучебные, так и логические. Интерактивность ИГС позволяет выстраивать индивидуализированные траектории как в освоении учебного материала, так и в развитии УУД. Весьма продуктивной оказывается организация работы в малых группах – в процессе групповой коммуникации она вынуждает учащихся к рефлексии своей деятельности по получению результата. Одновременно это способствует развитию коммуникативных УУД, направленных на сотрудничество в рамках решения поставленной проблемы.
Обобщая опыт разработки и проведения занятий, нами предложена структурно-функциональная модель развития УУД при обучении геометрии на ступени основного общего образования с использованием компьютерных средств наглядности. Концептуальной основой при разработке данной модели выступает принцип деятельностной наглядности. Содержание данного принципа как фактора формирования и развития регулятивных и познавательных универсальных учебных действий раскрывается в следующих компонентах:
1) создание учащимися визуальных моделей тех объектов, которые образуют проблемное поле;
2) осуществление материализованных действий с визуальными моделями, позволяющими сформировать проблемную ситуацию;
3) установление причинно-следственных связей между визуализированными компонентами моделируемой системы посредством допустимых ее трансформаций.
В качестве основных методических инструментов развития УУД используются методы проблемного обучения и организации групповой работы учащихся на уроке (см. [1], [2], [5]). В качестве технического средства реализации принципа деятельностной наглядности используются ИГС. Общие подходы к развитию УУД при обучении геометрии на ступени основного общего образования с использованием средств компьютерной наглядности представлены нами в виде следующей структурно-функциональной модели (рис. 1), состоящей из четырех блоков, выделенных в соответствии с общепринятыми принципами построения структурно-функциональных моделей: целевого, содержательного, операционного и контрольно-результативного.
Представленная модель проходила апробацию в МБОУ СОШ № 20 г. Нижний Тагил в 2013–2015 учебных годах. Для диагностики уровня сформированности УУД были использованы инструменты двух видов – технология тестирования и технология экспертных оценок (см. [4]). Они органично дополняют друг друга, позволяя уменьшить негативные проявления, присущие каждому из них, когда таковые применяются по отдельности. Объем выборки составил 79 учащихся 7-х классов. Результаты экспериментальной проверки модели развития УУД обработаны общепринятыми статистическими методами с использованием критерия согласия c2. Значения c2, полученные при сравнении показателей входной и итоговой диагностик уровня сформированности УУД для различных групп УУД, представлены в таблице 1.
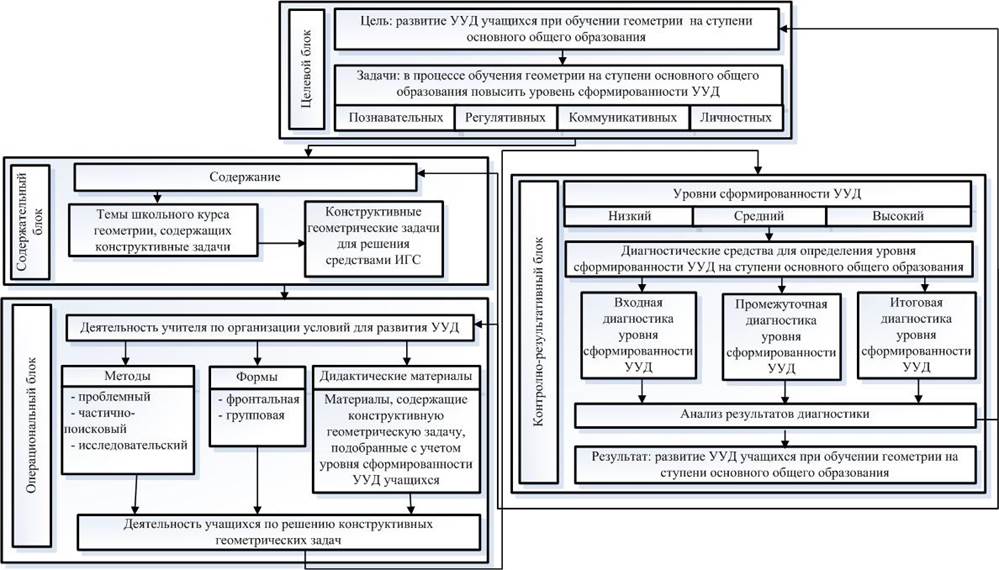
Рис. 1. Структурно-функциональная модель развития УУД при обучении геометрии на ступени основного общего образования с использованием средств ИГС
Таблица 1
Сравнение входной и итоговой диагностик уровня сформированности УУД учащихся
|
Группа универсальных учебных действий |
χ2 |
|
|
Познавательные УУД |
Общеучебные |
2,02 |
|
Логические |
10,89 |
|
|
Постановки и решения проблем |
19,47 |
|
|
Регулятивные УУД |
Целеполагание, анализ ситуации и планирование |
1,86 |
|
Самоконтроль и коррекция |
12,66 |
|
|
Волевые усилия и уровень самоорганизации |
6,21 |
|
|
Коммуникативные УУД |
0,60 |
|
По трем выделенным показателям (логические УУД, постановки и решения проблем, самоконтроля) достоверность различий составляет более 99%. Для УУД «Волевые усилия и уровень самоорганизации» достоверность различий составляет более 95%. Полученные результаты обосновывают результативность применения предложенной структурно-функциональной модели развития УУД учащихся с использованием средств деятельностной наглядности для четырех групп УУД – логических, постановки и решения проблем, самоконтроля и коррекции, волевые усилия и уровень самоорганизации.
Для общеучебных УУД достоверность различий составила около 65%; можно предположить, что здесь сказалась значительная разнородность входящих в эту группу УУД, поэтому требуется более детальное и дифференцированное исследование этой группы УУД. На развитии коммуникативных УУД сказываются многие факторы, в том числе возрастной, поэтому задача целенаправленного развития коммуникативных УУД нами не ставилась, но мы сочли полезным отслеживать изменения и в этой группе УУД.
Рецензенты:
Гейн А. Г., д.п.н., профессор Уральского федерального университета имени первого Президента России Б.Н. Ельцина, г. Екатеринбург;
Липатникова И. Г., д.п.н., профессор, зав. кафедрой теории и методики обучения математике Уральского государственного педагогического университета, г. Екатеринбург.



