Одной из причин недостаточного качества при шлифовании базовой торцовой сферической поверхности роликов конических подшипников является образование на обработанной поверхности отдельных царапин. Для выяснения возможных причин образования таких дефектов необходимо разработать геометрическую модель траектории царапины.
При обработке сферической поверхности ролика на ОАО «ЕПК Волжский» используется, в частности, специальный шлифовальный автомат модели SXK-5A [7].
Сферические торцы конических роликов обрабатываются методом шлифования на проход. До входа в зону контакта детали с кругом обрабатываемая поверхность имеет микрорельеф, образовавшийся на предыдущей операции или при выполняемом процессе шлифования [1]. Инструментом для данной операции служит вогнуто правленый шлифовальный круг, радиус которого идентичен со шлифуемым радиусом торца конического ролика. Шлифовальный круг правится на заданный радиус с помощью алмазного карандаша [3].
Существует ряд факторов, оказывающих существенное влияние на качество обработанной поверхности, таких как скорость подачи ролика, скорость шлифования, частота вращения ролика и шлифовального круга. Анализ, приведенный в работе [2], позволяет определить диапазон скоростей шлифования и соответствующие этому диапазону соотношения частот вращения для установления оптимального режима резания.
Для обеспечения стабильного параметра «длина ролика» и исключения влияния негативных факторов, возникающих при базировании заготовки на качество получаемой поверхности, исследовано влияние различных погрешностей, возникающих в процессе шлифования [6], а также разработаны математические модели припуска и скорости изменения его величины за время прохождения ролика через зону шлифования [8].
Цель работы
Разработать математическую модель траектории царапины, которую оставляет на базовой торцовой поверхности ролика вершина зерна шлифовального круга при обработке этой поверхности на шлифовальном станке модели SXK-5А.
В процессе обработки поверхности базового торца ролика на шлифовальном станке заготовка совершает следующие движения: вращение вокруг собственной оси против часовой стрелки с угловой скоростью ω; вращение вокруг оси сепаратора со скоростью vs. Математическая модель скорости подачи для любой точки базовой поверхности ролика представлена в работе [9].
Разработку математической модели траектории царапины выполняем путем разложения сложного движения ролика на элементарные составляющие и рассматриваем в следующем порядке: влияние только продольной подачи ролика на траекторию царапины; влияние только вращения ролика вокруг собственной оси на траекторию царапины; совместное влияние продольной подачи и вращения ролика вокруг собственной оси на траекторию царапины.
При разработке математической модели траектории царапины примем следующие начальные условия:
1) обрабатываемая поверхность ролика в проекции на плоскость представляет собой круг радиуса r;
2) технологическую выточку на базовой торцовой поверхности ролика не учитываем;
3) декартову систему координат располагаем в центре окружности поверхности ролика с направлением осей, указанных на рисунке 2;
4) считаем, что царапина образовалась от вершины зерна, движущегося прямолинейно со скоростью v в направлении, противоположном направлению оси ординат;
5) учитывая, что обрабатываемая поверхность — сфера, а не плоскость, площадью контакта зерна с обрабатываемой поверхностью ролика будет являться не вся сферическая поверхность, а только ее отдельный участок (рис. 1), площадь которого зависит от глубины резания и величины снимаемого припуска [5].
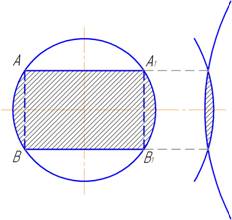
Рис. 1.Схема площади контакта зерна (АА1В1В) с обрабатываемой поверхностью
Определим траекторию царапины, образованной вершиной зерна, касающейся базовой поверхности ролика в точке А с координатами (0, уА), с учетом влияния только продольной подачи ролика (рис. 2).
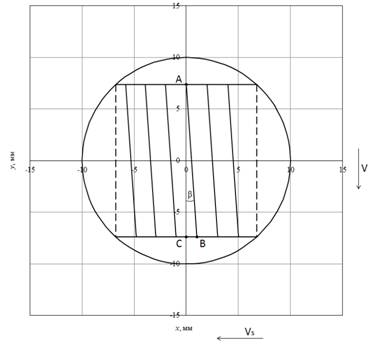
Рис. 2. Траектории движения зерен шлифовального круга
с учетом только продольной подачи ролика
В результате перемещения окружности влево вершина зерна выйдет из контакта с обрабатываемой поверхностью в точке B с координатами (xВ; yВ). Перемещение вдоль оси абсцисс определяется скоростью продольной подачи vs, вдоль оси ординат – скоростью шлифования v. Тогда отрезки
CB = xВ – xА = vsτmax, AC = yА – yВ = vτmax, (1)
где τmax – полное время контакта зерна с обрабатываемой поверхностью.
Из формулы (1):
τmax = ![]() ; τmax =
; τmax = ![]() .
(2)
.
(2)
Приравняв правые части равенств (2):
![]() =
= ![]() .
(3)
.
(3)
Координаты точки выхода зерна находим из (1):
xВ = xА + vsτmax; yВ = yА – vτmax. (4)
Координаты i-ой точки в момент времени τi находим по формулам:
xi = xА + vsτi; yi = yА – vτi. (5)
Так как v и vs – величины постоянные, царапина без учета вращения заготовки ролика вокруг своей оси будет представлять собой прямую линию.
Рассмотрим траекторию движения зерна только при вращении ролика вокруг своей оси с заданной угловой скоростью ω (рис. 3).
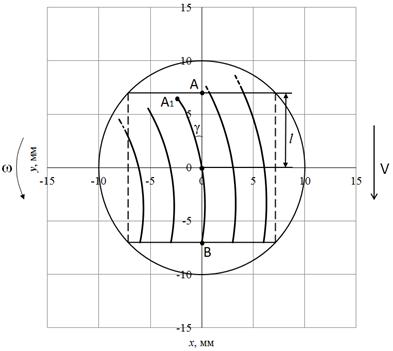
Рис. 3. Траектории движения зерен шлифовального круга
с учетом только вращения ролика вокруг собственной оси
Рассмотрим точку А с координатами (0; l), расположенную на оси симметрии торца ролика. За время контакта τi точка А повернется на угол γ и сместится по оси абсцисс и ординат в результате круговой подачи заготовки (точка А1) (рис. 3).
Поворот точки А на угол γ определяется угловой скоростью вращения заготовки вокруг своей оси ω:
γ = ωΔτi . (6)
Угловую скорость определяем по числу оборотов ролика вокруг своей оси n:
ω = 2πn. (7)
Время на изменение положения точки Δτi в результате вращения заготовки будет равно:
Δτi = τmax – τi. (8)
Так как время, за которое точка А окажется в положении А1, равно максимальному времени обработки, следовательно, Δτ1 = τmax.
Полное время контакта вершины рассматриваемого зерна с металлом для осевого сечения будет равно:
![]() .
(9)
.
(9)
Координаты точки А1 с учетом знаков вычисляем по формулам:
![]() (10)
(10)
Точка B не изменит своего положения, потому что при τi = 0 угол поворота γ также будет равен нулю. Координаты точки B: xB = 0; yB = –l.
При движении зерна со скоростью v изменяется не только угол поворота каждой рассматриваемой точки, но и радиус поворота, который для каждой i-ой точки равен yi.
Для нахождения координат i-ой точки траектории движения зерна задаем значения точки по оси ординат в диапазоне: -l ≤ yi < у1.
Для каждой рассматриваемой точки:
уi = l –vτi. (11)
Из (11) выразим момент времени τi:
![]() (12)
(12)
Подставив (12) в (8), получим:
![]() (13)
(13)
Координаты i-ой точки траектории движения по оси абсцисс вычисляем по формуле:
![]() (14)
(14)
Рассмотрим произвольную точку Аi с координатами (хi; yi).
Для хi < 0 координаты i-ой точки траектории движения зерна с учетом начального угла положения точки относительно оси вращения вычисляем по формулам:
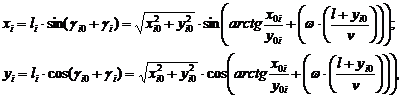 (15)
(15)
с учетом знаков тригонометрических функций – для xi со знаком «–» во II четверти и со знаком «+» в III четверти; для уi со знаком «+» во II четверти и со знаком «–» в III четверти.
Для хi > 0 координаты i-ой точки траектории движения зерна с учетом начального угла положения точки относительно оси вращения вычисляем по формулам:
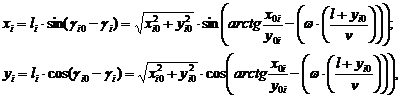 (16)
(16)
с учетом знаков тригонометрических функций для xi и уi со знаком «+» в I четверти и со знаком «–» в IV четверти.
Рассмотрим геометрическую модель царапины с учетом совместного действия продольной подачи и вращения ролика вокруг собственной оси.
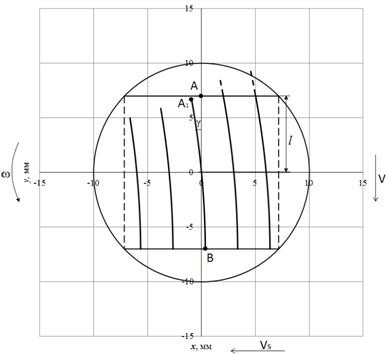
Рис. 4. Траектории движения зерен шлифовального круга
с учетом продольной подачи ролика и его вращения вокруг собственной оси
Первоначальным этапом смещения точки траектории царапины является продольная подача заготовки, вторым фактором является смещение точки с новыми координатами, происходящее в результате вращения заготовки вокруг своей оси.
Вычисление координат i-ой точки в результате продольного перемещения со скоростью подачи vs осуществляется по формулам (5).
Новые координаты i-ой точки в результате вращения заготовки вокруг своей оси находим по формулам (15, 16)
Таким образом, координаты точек перемещения зерна с учетом совместного влияния продольного перемещения и вращения заготовки вокруг своей оси находим путем сложения этих двух движений:
для –хi ≤ хi < 0:
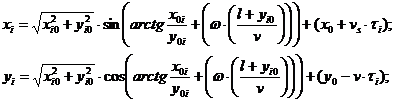
![]() (17)
(17)
для хi ≥ хi > 0:
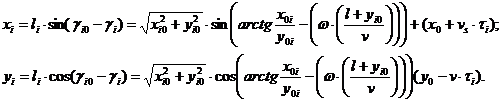 (18)
(18)
В точке выхода изменение координат происходит только в результате продольной подачи. Фактор вращения в данном случае влияния не оказывает.
Выводы
Получены формулы для разработки траектории движения царапины, которую оставляет на базовой торцовой поверхности ролика вершина зерна шлифовального круга при обработке этой поверхности на сферошлифовальном станке модели SXK-5А, с учетом продольной подачи ролика и вращения его вокруг собственной оси. На основании полученных формул разработаны геометрические модели траектории движения царапины зерна с учетом заданных условий. В результате получены закономерности изменения данной траектории, зависящие от применяемых режимов обработки торцевой поверхности ролика.
Полученные функциональные зависимости дают возможность сравнительного анализа геометрической модели траектории движения зерна с опытными данными, полученными в результате практического нахождения траектории движения царапины на торцовой поверхности ролика.
Рецензенты:Санинский В.А., д.т.н., профессор кафедры «Технология и оборудование машиностроительных производств» Волжского политехнического института (филиал) ФГБОУ ВПО «Волгоградский государственный технический университет, г. Волжский.
Пушкарев О.И., д.т.н., профессор кафедры «Общетехнические дисциплины», Волжский институт строительства и технологий (филиал) ФГБОУ ВПО «Волгоградский государственный архитектурно-строительный университет», г. Волжский.



