(1)
(2)
(3)
где 
- фиксированная точка
интервала 
, 
и 
- положительные числа. Коэффициент 
в уравнении (1) предполагается отличным
от нуля хотя бы в одной точке отрезка 
.
Пусть 
и 
- решения дифференциальных задач
(4)
,
(5)
соответственно. Приведём формулировки теорем, в которых даются необходимые и достаточные условия однозначной разрешимости задачи (1)-(3).
Теорема 1. Пусть 
, 
и выполнено условие
. (6)
Тогда задача (1)-(3) однозначно разрешима
в классе 
, и её решение представимо
в виде
. (7)
Теорема 2. Пусть , и функция 
такова, что для всех 
выполнено
условие
. (8)
Тогда решение задачи (1)-(3) существует,
единственно и принадлежит классу .
Эти теоремы доказаны в работах 
, 
. В дальнейшем будем считать, что
выполнены условия В: 
, .
Имеет место
Теорема 3. Если 
удовлетворяют условию В и выполнено (8), то решение
задачи (1)-(3) принадлежит классу 
.
Доказательство этой теоремы следует из однозначной
разрешимости задач (4) и (5) в классе при
выполнении условий В, и представления решения в виде (7).
Введём на отрезке
равномерную сетку 
. Шаг 
сетки
выберем меньше половины меньшего из отрезков 
.
Номер 
выберем из
условия 
. Используем для сеточной функции 
, определённой на 
,
обозначение 
:
. Дифференциальную задачу (4)
аппроксимируем конечно-разностной схемой
,
(9)
,
,
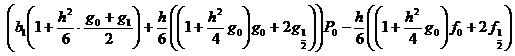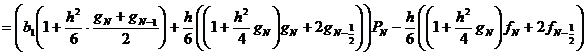где 
,
а дифференциальную задачу (5) - конечно-разностной схемой
, (10)
,
,
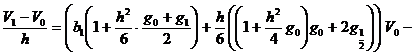
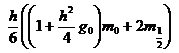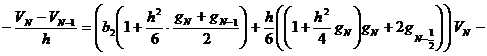
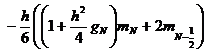где 
.
Конечно-разностные схемы (9) и (10) аппроксимируют задачи (4)
и (5) соответственно, с точностью 
, что не трудно
показать с помощью разложений по формуле Тейлора.
Пусть
, (11)
полином Лагранжа третьей степени, проведённый через точки
,
,
, 
. Коэффициенты Лагранжа вычисляются по
формулам:
, 
,
, 
. (12)
Введём обозначение 
и покажем, что 
аппроксимирует значение 
с точностью . В
силу равенств 
, и ограниченности
коэффициентов Лагранжа, 
. Поскольку полином 
аппроксимирует функцию 
на отрезке 
с
точностью , что следует из известной оценки
погрешности полинома Лагранжа , то
найдётся положительная постоянная 
, не зависящая от , что
. (13)
Аналогично, 
аппроксимируются
величиной 
с точностью ,
следовательно, найдётся постоянная 
, что
. (14)
В качестве приближённого решения задачи (1)-(3) выберем
сеточную функцию :
, 
.
(15)
Имеет место
Теорема 4. Пусть выполнены условия В и (8). Тогда сеточная
функция 
, определённая по формуле (15), сходится при 
к
решению 
задачи (1)-(3) со скоростью в равномерной метрике.
Доказательство. Используя
представление (7) решения задачи (1)-(3), получим оценку погрешности 
в равномерной метрике:
.
(16)
Оценим слагаемые в правой части (16). Сначала оценим 
. Отметим, что в силу принципа максимума
разностной краевой задачи третьего рода 
,
решения задачи (10) положительны. Перепишем уравнение (10) в виде
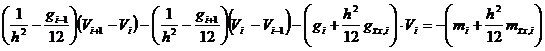. (17)
Пусть положительный максимум 
функции
достигается в точке 
, т.е. 
, где 
. Тогда, в силу 
,
, из (17) получаем оценку
.
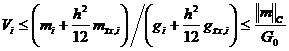Если 
, то из левого краевого условия (10)
следует оценка:
.
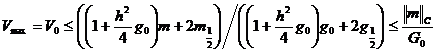Если 
, то из правого краевого
условия (10) следует оценка:
.
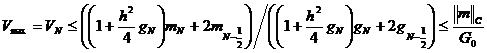Таким образом, для решения задачи (10) имеет место оценка:
. (18)
С учётом аппроксимации порядка разностной
схемы (10) на решении задачи (4), найдётся положительная постоянная 
, что 
. (19)
Также найдется положительная постоянная 
,что
. (20)
Введём обозначение 
.
Если выполнено условие (8), то, как следует из принципа максимума
третьей краевой задачи для оператора Штурма-Лиувилля 
,
, при этом имеет место оценка
. (21)
Получим нижнюю оценку выражения 
.
Пусть 
- шаг сетки, что 
.
Тогда при 
оценка (13) принимает вид 
, откуда следует:
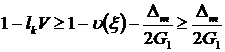. (22)
Применяя оценки (13), (14), (18)-(22) из (16) получаем:
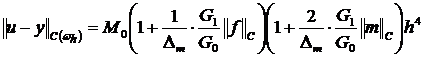. (23)
Из оценки (23) следует утверждение теоремы 4.
Рецензенты:
Шхануков-Лафишев М.Х. д.ф.-м.н., профессор, ФГБУН Институт информатики и проблем регионального управления Кабардино-Балкарского научного центра РАН, г. Нальчик;
Ашабоков Б.А,, д.ф.-м.н., профессор, Высокогорный Геофизический Институт, г. Нальчик.