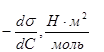Данные о свойствах растворов поверхностно-активных веществ (ПАВ) представляют определенный интерес для биологии, что связано со способностью ПАВ адсорбироваться на границах раздела и тем самым, в соответствии с законами кинетики, во много раз увеличивать скорость процессов в биологических системах.
Важнейшей адсорбционной характеристикой веществ, определяющей многие их свойства и области применения, является поверхностная активность. Природные ПАВ имеют преимущества, так как зачастую сами выполняют роль лекарственных средств или БАД и не обладают токсичностью.
Цель наших исследований – изучение поверхностной активности водорастворимых полисахаридов, выделенных из семян льна, определение параметров адсорбционного слоя при адсорбции ПАВ на границе раздела «газ-жидкость».
Материалы и методы
Выделение полисахаридов (ПС) семян льна проводили по методу Н.К.Кочеткова и M.Sinnera [4, 6]. Для определения поверхностного натяжения использовали прибор Ребиндера метод наибольшего давления при проскакивании пузырьков воздуха в раствор и растворитель [2].
Экспериментальная часть
Сырье экстрагировали водой при комнатной температуре и постоянном перемешивании в течении 12 часов (соотношение сырья и экстрагента - 1:15). Полученное извлечение фильтровали, полисахариды из фильтрата осаждали двойным объемом 95% спирта этилового. Водно-спиртовую смесь центрифугировали в течение 15 минут при частоте вращения 3000 об/мин. Осадок переносили в выпарительную чашку и высушивали в термостате при температуре 40ºС до постоянной массы.
Для изучения поверхностноактивных свойств ПС готовили серию водных растворов ПС в области концентраций 0,01-0,5% и измеряли с использованием прибора Ребиндера наибольшее давление при проскакивании пузырьков воздуха в раствор и растворитель [1,2].
Результаты и их обсуждение
Расчет величины поверхностного натяжения растворов
Расчет величины поверхностного натяжения растворов при температуре опыта (20ºС) проводили по уравнению:
,
где σх и σ0 – поверхностное натяжение при 20ºС раствора ПС и воды (σ0 = 72,75∙10-3 Н/м);
hx, h0 – давление пузырьков воздуха для исследуемого раствора и воды [4].
Такой вид уравнения справедлив при условии равенства плотностей воды и разбавленных водных растворов ПС. Результаты эксперимента приведены в таблице 1.
Таблица 1
Поверхностное натяжение водных растворов ПС в зависимости от концентрации
|
С, % |
С∙104, моль/м3 |
h, мм ст.ж. |
σ·103, Н/м |
|
Н2О |
0 |
69 |
72,75 |
|
0,0096 |
2,14 |
66 |
69,58 |
|
0,0190 |
4,28 |
62 |
65,37 |
|
0,0385 |
8,56 |
61 |
64,31 |
|
0,0770 |
17,12 |
55 |
57,99 |
|
0,1540 |
34,24 |
52,5 |
55,35 |
По экспериментальным данным построена изотерма поверхностного натяжения σ = f (С) (рисунок 1).
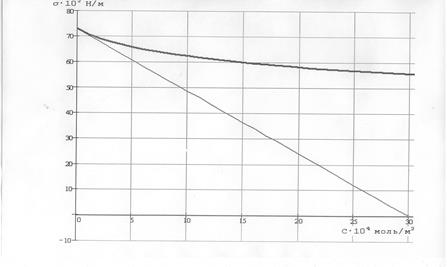
Рис.1. Изотерма поверхностного натяжения
Полученные результаты свидетельствуют о наличии поверхностной активности исследуемых ПС. Поверхностная активность ПС 
находится графическим методом путем проведения касательной к изотерме поверхностного натяжения в точке, отвечающей бесконечно разбавленному раствору:
Расчет величины поверхностного избытка
Обработка экспериментальной зависимости σ=f(С) позволяет рассчитать величину удельной адсорбции ПС (поверхностного избытка ) по уравнению Гиббса:
,
где R – универсальная газовая постоянная (
), Т – температура (293 К).
Для этого методом аналитического дифференцирования определили 
, используя эмпирическое уравнение Шишковского, которое дает зависимость σ =f(С) в аналитическом виде:
,
где А и В – эмпирические константы; σ0 и σ – поверхностное натяжение растворителя и раствора соответственно [3,5].
Нелинейная зависимость f(x), проходящая через «облако» узловых точек с наименьшей среднеквадратичной погрешностью отклонения выполняется в процессе регрессии статистической обработки данных.
Используемый метод заключается в решении системы нелинейных уравнений, в которую входят приближенные равенства f(С0,A,B) = y0 и выражение с функцией Minerr(A,B), возвращающей значения A и B, при которых система решается с минимальной среднеквадратичной зависимостью средствами MathCard.
Исходные данные заданы векторами:
Введем начальные приближения для параметров: σ0=72.75·10-3 Н/м;
A:= 104 моль/м3; B:= 10-3 Н/м
и зададим экспоненциальную функцию регрессии
f(C,A,B):= σ0-A·ln(AC+1)
Само решение реализуется следующим блоком решения:
Given
f(C0,A,B) = у0; f(C1,A,B) = у1; f(C2,A,B) = у2; f(C3,A,B) = у3; f(C4,A,B) = у4; f(C5,A,B) = у5.
Теперь можно проверить решение:
A = 0.347·104 моль/м3; B = 6.9999∙10-3 Н/м
Результаты расчетов приведены в таблице 2.
Таблица 2
Результаты определения удельной адсорбции ПС в зависимости от концентрации раствора
|
С∙104, моль/м3 |
|
Г·106, моль/м2 |
|
|
|
2,14 |
13,94 |
1,225 |
0,816 |
0,467 |
|
4,28 |
9,77 |
1,717 |
0,582 |
0,234 |
|
8,56 |
6,12 |
2,151 |
0,465 |
0,117 |
|
17,12 |
3,50 |
2,460 |
0,407 |
0,058 |
|
34,24 |
1,89 |
2,650 |
0,377 |
0,029 |
Подстановка в уравнение Гиббса производной поверхностного натяжения по концентрации 
, найденной из уравнения Шишковского, приводит к уравнению изотермы адсорбции Ленгмюра: 
В теории мономолекулярной адсорбции Ленгмюра предполагается, что силы, вызывающие адсорбцию, имеют радиус действия, соизмеримый с размером молекул. Поэтому толщина адсорбционного слоя не превышает размеры молекул – адсорбция мономолекулярна.
Характерной особенностью изотермы адсорбции Ленгмюра является участок постоянной адсорбции 
= 2,874∙10-6 моль/м2 (при С→ ∞), соответствующий образованию на поверхности раздела насыщенного монослоя из молекул адсорбирующегося вещества.
Признаком мономолекулярного характера адсорбции является применимость к опытным данным как уравнения Ленгмюра, так и уравнения Шишковского.
Проверку применимости уравнения Шишковского проводят, рассчитав по полученным константам А и В поверхностное натяжение (σ) растворов различной концентрации (С). Результаты расчетов приведены в таблице 3.
Таблица 3
Поверхностное натяжение растворов, определенное экспериментально и по уравнению Шишковского
|
С∙104, моль/м3 |
σ·103 эксперимент, Н/м |
σ·103 по Шишковскому , Н/м |
|
2,14 |
69,58 |
68,86 |
|
4,28 |
65,37 |
66,38 |
|
8,56 |
64,31 |
63,10 |
|
17,12 |
57,99 |
59,19 |
|
34,24 |
55,35 |
54,86 |
Удельную адсорбцию можно вычислить по уравнению изотермы адсорбции Ленгмюра по константам А и В (таблица 4).
Таблица 4
Значения удельной адсорбции ПС, рассчитанные по уравнениям Гиббса и Ленгмюра
|
С∙104, моль/м3 |
Г·106 по Гиббсу, моль/м2 |
Г·106 по Ленгмюру, моль/м2 |
|
2,14 |
1,225 |
1,225 |
|
4,28 |
1,717 |
1,717 |
|
8,56 |
2,151 |
2,150 |
|
17,12 |
2,460 |
2,460 |
|
34,24 |
2,650 |
2,650 |
Полученные результаты позволяют сделать вывод о применимости теории мономолекулярной адсорбции.
Расчет площади (S), занимаемой молекулой ПС в адсорбционном слое, толщины адсорбционного слоя (l) и объема молекулы (V.)
Определить величину предельного поверхностного избытка Г∞ =2,874·10-6 моль/м2 можно также, построив график изотермы адсорбции в координатах 1/Г от 1/С (рисунок 2).
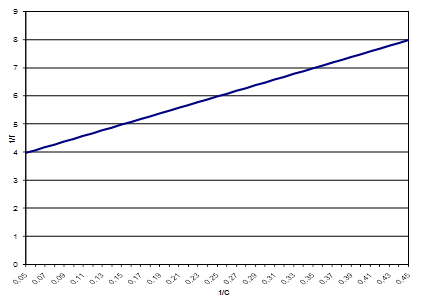
Рис.2. Изотерма поверхностного натяжения в координатах 1/Г = f(1/С)
Экстраполируя его до пересечения с осью ординат, получаем отрезок, равный обратной величине предельного поверхностного избытка 1/Г∞. Результаты графического определения Г∞ сопоставимы с величиной, рассчитанной по уравнению Ленгмюра. Определение Г∞ позволяет рассчитать площадь (S), занимаемую молекулой ПС в адсорбционном слое, толщину адсорбционного слоя (l) и объем молекулы (V). Расчет проводили по уравнениям:
; 
; 
,
где NA - число Авогадро (6,02∙1023моль-1), М – средняя молярная масса полисахаридов (450кг/моль), ρ – плотность раствора, принятая равной плотности растворителя (1∙103кг/м3).
S = 57,8·10-20 м2 = 57,8 Å2
l = 12933·10-10 м = 12933 Å
V = 747527·10-30 м3 = 747527 Å3
Выводы
Установлено наличие поверхностной активности полисахаридов семян льна в водных растворах. Показано соответствие экспериментальных значений поверхностного натяжения водных растворов ПС и значений, рассчитанных по уравнению Шишковского, что говорит о применимости уравнения Шишковского во всем диапазоне концентраций. Показана идентичность величин удельной адсорбции полисахаридов, рассчитанных по уравнениям Гиббса и Ленгмюра, что позволяет сделать вывод о применимости теории мономолекулярной адсорбции. Определены параметры адсорбционного слоя ПС в водном растворе.
Рецензенты:
Коновалов Д.А., д.ф.н., профессор, заведующий кафедрой фармакогнозии, Пятигорский медико-фармацевтический институт – филиал ГБОУ ВПО ВолгГМУ Минздрава России, г. Пятигорск;
Компанцев В.А., д.ф.н., профессор кафедры неорганической, физической и коллоидной химии, Пятигорский медико-фармацевтический институт – филиал ГБОУ ВПО ВолгГМУ Минздрава России, г. Пятигорск.