Главной частью подобных систем является её привод, представляющий собой электромагнит. Электромагниты в своем составе имеют подвижную и неподвижную части магнитопровода и, как минимум, одну рабочую катушку. В ходе их эксплуатации в рабочей катушке протекает ток, создается рабочий магнитный поток в магнитопроводе, приводящий в движение подвижную его часть. Величина магнитного потока определяется магнитными свойствами и конструкцией частей магнитопровода, количеством витков в рабочей катушке и величиной протекающего тока. В настоящее время для диагностики электромагнитов проводят измерения их механических, электрических и магнитных характеристик. Для получения каждой из этих характеристик требуется применить свои средства испытания и, как правило, демонтировать электромагнит из системы. Известен подход [7], при котором для электромагнитов постоянного тока используют всего одну интегральную характеристику – зависимость магнитного потока в магнитопроводе от тока в катушке в ходе выполнения им стандартной операции. Эта характеристика называется вебер-амперной характеристикой рабочего цикла (ВАХРЦ), в зависимости от вида которой, можно идентифицировать тип неисправности.
Для устройств переменного тока предлагается описанный ниже метод. На не демонтированный из электротехнического устройства электромагнит подают синусоидальное напряжение, амплитуда которого ступенчато изменяется от нулевого значения до номинального и обратно (рисунок 1).
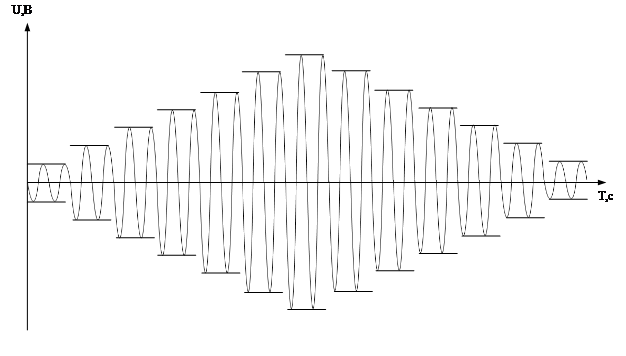
Рис.1. Подаваемое на устройство переменного тока синусоидальное напряжение
При этом электромагнит совершает рабочий цикл, преодолевая сопротивление исполнительных механизмов, соединенных с ним. На каждой ступени напряжения измеряется частная вебер-амперная характеристика (ВАХ) и амплитуда тока. Фиксируя местоположение конечных точек частных ВАХ получаем ВАХРЦ (рисунок 2).
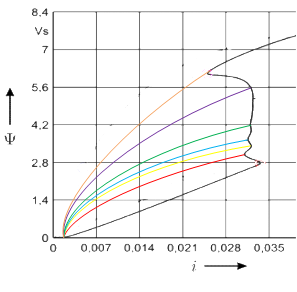
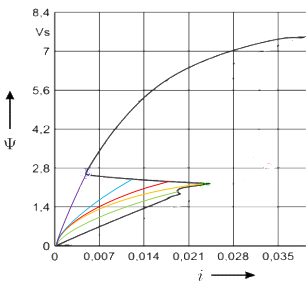
Рис.2. Методика получения ВАХРЦ
Для определения частных ВАХ будем использовать метод натурно-модельных испытаний [1-6, 8-10], объединяющий измерение на физическом объекте и моделирование в персональном компьютере при помощи специального программного обеспечения. Алгоритм натурно-модельных испытаний применительно к этой задаче состоит в следующем: на электромагнит подается синусоидальное напряжение и с помощью датчиков напряжения и тока производятся измерения подаваемого на рабочую катушку напряжение и ток в ней. Измеренные напряжение и ток поступают в персональный компьютер, где в модель электромагнита вводится напряжение и ею эмулируется выходной ток. С помощью оптимизационного алгоритма добиваются совпадения измеренного и эмулированного моделью электромагнита токов.
Для получения модели описывающей работу электромагнита запишем уравнение цепи:
![]() .
.
где ![]() – напряжение, приложенное
к катушке электромагнита, Ua – амплитуда напряжения,
– напряжение, приложенное
к катушке электромагнита, Ua – амплитуда напряжения, ![]() – ток протекающий в рабочей катушке электромагнита, I(2m-1) – амплитуда (2m-1) – ой гармоники тока, n – количество гармоник
тока,
– ток протекающий в рабочей катушке электромагнита, I(2m-1) – амплитуда (2m-1) – ой гармоники тока, n – количество гармоник
тока, ![]() – представленная в виде полинома ВАХ электромагнита.
– представленная в виде полинома ВАХ электромагнита.
Перепишем его с учетом выражений для тока, напряжения и ВАХ:
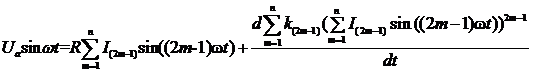 .
.
Модель электромагнита построена в программном пакете Labview, внешний вид пользовательского интерфейса программы приведен на рисунке 3.
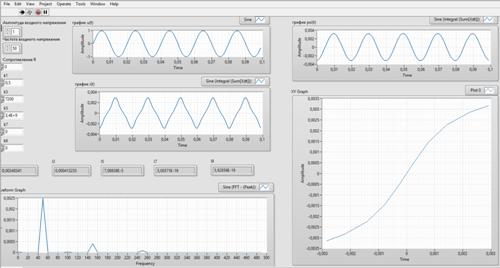
Рис.3. Пользовательский интерфейс программы-эмулятора
Для работы модели необходимо ввести исходные
данные: амплитуду Ua, и частоту ω
входного напряжения, а также коэффициенты аппроксимации ВАХ ![]() .
На выходе программы-эмулятора формируются значения гармоник тока I(2m-1), изображения графиков изменения напряжения «u(t)», тока «i(t)», потока «psi(t)», а также ВАХ «XY Graph» и спектрограмма тока «Waveform Graph».
.
На выходе программы-эмулятора формируются значения гармоник тока I(2m-1), изображения графиков изменения напряжения «u(t)», тока «i(t)», потока «psi(t)», а также ВАХ «XY Graph» и спектрограмма тока «Waveform Graph».
Оптимизационный алгоритм управляющей программы использует метод симплекс-оптимизации. Программа симплекс-оптимизации построена в программном пакете Turbo Delphi. Она расчитана на работу с 2-5 факторами. Интерфейс программы с примером решения двухфакторной задачи представлен на рисунке 4.

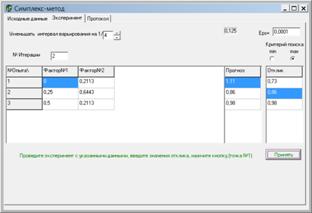

Рис.4. Программа симплекс-оптимизации
Во вкладке «Исходные данные» задается количество факторов, на основании чего формируется таблица, в которой необходимо задать центр плана, интервал варьирования и пределы изменения факторов. После чего программа составляет схему симплекса в нормированных единицах. Во вкладке «Эксперимент» выводятся координаты проведения эксперимента в физических величинах и заносятся его результаты, задается цель оптимизации (минимум или максимум) и значение различий отклика в вершинах симплекса, с достижением которого движение симплекса заканчивается. На каждом шаге программа определяет «наихудшую» точку и указывает пользователю условия следующего эксперимента. В случае вращения симплекса вокруг одной из вершин, интервал варирования уменьшится кратно величине заданной в поле «уменьшить интервал варьирования». Во вкладке «Протокол» отражаются все пройденные шаги.
Факторами являются коэффициенты аппроксимации ВАХ k2m-1, а функцией цели – площадь разности токов ![]() – экспериментально полученного и
– экспериментально полученного и ![]() – полученного из модели за половину
периода. При минимуме этой разности коэффициенты k2m-1 будут описывать искомую
ВАХ.
– полученного из модели за половину
периода. При минимуме этой разности коэффициенты k2m-1 будут описывать искомую
ВАХ.
Проанализируем выражение функции цели:
![]()
Произведя преобразования получим: ![]()
Значит, в качестве функции цели следует взять сумму разности гармоник умноженную на коэффициент 2m-1.
На рисунке 5 приведены истинная и полученная на модели ВАХ на первой итерации симплекс-оптимизации. Видно, что формы тока физического объекта и модели существенно различны.
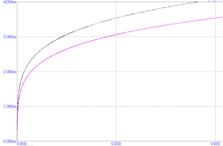
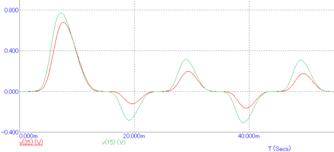
Рис.5. ВАХ и токи, полученные на первой итерации
После семидесяти двух итераций, форма тока эмулятора приблизилась к форме тока физического объекта. При этом различия ВАХ составили 0,1%. Это означает, что полученная на последней итерации ВАХ и является искомой.
Проведены исследования влияния погрешности измерения гармоник тока на погрешность ВАХ. С использованием теории планирования многофакторного эксперимента, получена зависимость погрешности алгоритма от значений первых пяти нечетных гармоник тока:
![]()
Значения гармоник тока варьировались в интервале ±4,4%, погрешность получения ВАХ не превысила 1%. Обработка результатов эксперимента осуществлялась с помощью программного продукта Statistica 10.
Результаты работы получены при поддержке гранта РФФИ № 15-38-20652 «Развитие теории бессенсорных прогнозирующих методов управления и диагностики электроприводов» с использованием оборудования ЦКП "Диагностика и энергоэффективное электрооборудование" ЮРГПУ (НПИ).
Рецензенты:Савелов Н.С., д.т.н., профессор, ФГБОУ ВПО «Южно-Российский политехнический университет им. Платонова», г. Новочеркасск;
Елсуков В.С., д.т.н., профессор, ФГБОУ ВПО «Южно-Российский политехнический университет им. Платонова», г. Новочеркасск.



