Сфера услуг в настоящее время стремительно развивается. Потребители нуждаются в качественных транспортных, медицинских, финансовых (3) и прочих услугах.
В образовании, которое также является специфической услугой, в настоящее время осуществляется переход к компетентностной парадигме, позволяющей повысить эффективность образовательного процесса и приблизить качество подготовки специалистов к возросшим требованиям работодателей /1/.
В федеральных образовательных стандартах третьего поколения предписано формирование рабочих программ и учебных планов осуществлять на основе соответствующих наборов профессиональных и общекультурных компетенций. В работе (4)авторами была описана методика формирования набора дидактических единиц, реализующих ту или иную профессиональную компетенцию на основе некоторого набора начальных компетенций и базы дидактических единиц. Эта методика предполагает использование соответствующим образом сконструированной и обученной нейронной сети. Для обучения такой нейронной сети, как известно, необходим достаточно большой набор обучающей выборки, что не всегда возможно обеспечить для всех компетенций (особенно это касается профессиональных компетенций). Поэтому опишем другой возможный вариант решения той же задачи.
Предположим, нам нужно сформировать учебный план, реализующий ту или иную компетенцию и имеющий объем Vзачетных единиц. У нас имеется база из N дидактических единиц, каждая из которых имеет объем vi (i=1,..N) иотносительную полезность ci применительно к рассматриваемой компетенции.
Введем Nбулевых переменных xi:
![]()
Заметим, что по смыслу дидактическая единица – это целостный учебный элемент, который нельзя декомпозировать на более простые элементы без потери смысла. Поэтому такие единицы либо входят в план целиком, либо не входят вообще.
Тогда целевая функция задачи формирования плана – это максимизация суммарной полезности:
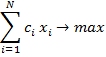
с очевидными ограничениями:
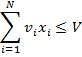
В такой постановке эта задача решается методами целочисленного программирования, которые широко используются в моделировании управленческих и экономических систем (5).
После формирования оптимального набора единиц (учебных элементов) следующей по важности задачей является задача определения правильной (эффективной) последовательности их изучения. Для решения этой задачи введем понятие «близость дидактических единиц» на основе представления о дескрипторах. Дескриптором будем считать ключевое слово (понятие, термин и т.п.), имеющий вполне определенную семантику в контексте изучаемого учебного элемента (например, «база данных», «имитационная модель», «класс объектов» и т.д.).
Определим относительную близость дидактических единиц di и dj в виде:
![]()
где Nij– число совпадающих дескрипторов в единицах di и dj, aNi; и Nj– соответственно, общее число дескрипторов в них. Очевидно, что в общем случаеri≠ rj.
Отметим, что если ri ~ rj> 0,5 , то соответствующие единицы имеют слишком много «пересечений» и правомерно рассматривать вопрос об их объединении. Наоборот, если ri ~ rj<0,1, то единицы можно считать независимыми, в учебных планах ставить их параллельно (например, как базовые).
Введем понятие меры ассоциации Sij единиц di и dj:
![]()
Теперь с помощью введенных величин можно проанализировать относительный вклад тойили иной дидактической единицы в учебный план (рабочую программу), а также установить предположительный порядок их изучения. В самом деле, если ri<<rj, то это значит, что смысловое поле единицы di много шире, чем у dj. Тогда, скорее всего, первая единица является базовой и ее следует изучать первой, а вторая единица – уточняет и (или) развивает первую в определенном контексте или направлении.
Если ri ~ rjи при этом Sijмало, то рассматриваемые единицы практически независимы, и их можно изучать в любой последовательности или параллельно. Наконец, если ri ~ rjи при этом Sij не мало, то соответствующие учебные элементы имеют много общих дескрипторов, и при этом их смысловые поля сравнимы. В этом случае эти единицы должны в учебных планах и программах стоять рядом, но порядок изучения должен быть определен исходя из каких-то дополнительных критериев.
Заметим, что значения Sij, также как riи rj находятся в интервале (0, 1), и изменение этого параметра при соответствующих изменениях riи rj небольшие. Поэтому на практике значительно удобнее пользоваться другой величиной –коэффициентом улучшения ассоциации Кij:
![]()
Дальнейший алгоритм выглядит примерно так: определяется (исходя из некоторых соображений) базовая дидактическая единицаd1. Определяются все коэффициенты К1jдля всехj> 1. Из них находится максимальный (допустим d1m), и выстраивается следующая последовательность изучения дидактических единиц: di→dm. Далее, заменяем m на 2 и рассматриваем все коэффициенты K2j при j>2, определяем максимальный и продолжаем выстраивать цепочку последовательностивхождения учебных элементов в программу (план).
Понятно, что таким образом можно сформировать только линейную последовательность изучения учебных элементов, однако в ряде случаев (и нередко) при формировании учебных планов одна и та же дидактическая единица используется как «стартовая позиция» для двух и более дидактических единиц (см. рис.1). В этом случае можно предложить следующий алгоритм: после нахождения двух близких к d1 единиц (d2 и d3), определяется их относительная близость K23. Если эта величина мала, но при этом r2и r3значительны, то это может означать, что единицы d2 и d3 используют разные общие с d1
наборы дескрипторов. Это и будет служить веским доводом в пользу того, что обе единицы базируются на d1 и могут изучаться параллельно, то есть, образуют дерево процесса обучения с двумя ветками. Таким же образом можно построить учебные планы (программы) с любым числом ветвей.
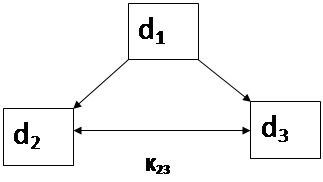
Рис.1.Разветвления в порядке следования учебных элементов
Поясним описанный выше алгоритм на простом примере. В таблице 1 приведен фрагмент текстового файла, содержащего пять учебных элементов с соответствующими дескрипторами для курса «Анализ данных».
Таблица 1
Учебные элементы и дескрипторы для курса «Анализ данных»
|
Номер элемента |
Название элемента |
Набор дескрипторов |
|
EL01 |
Технология Data Mining |
Хранилище данных, оптимизация, машинное обучение, кластеризация, классификация, ассоциации, шаблоны, деревья решений, анализ рисков, скоринг, профайлинг, прогнозирование, регрессионный анализ, корреляционный анализ, временной ряд, консолидация данных, DataMining, нейронные сети, статистика |
|
EL02 |
Введение в консолидацию данных |
Консолидация данных, извлечение данных, преобразование данных, загрузка данных, очистка данных, обогащение данных, хранилище данных, витрины данных, оценка качества данных |
|
EL03 |
Технология ETL |
Извлечение данных, очищение данных, преобразование данных, загрузка данных, агрегирование данных, перевод значений, поток данных |
|
EL04 |
Концепция хранилища данных |
Хранилище данных, извлечение данных, очищение данных, преобразование данных, загрузка данных, витрины данных, метаданные, агрегирование данных, обогащение данных, оценка качества данных, интегрированные данные, детализация данных, предметно-ориентированные данные, хронология данных, неизменяемость данных |
|
EL05 |
Введение в кластеризацию данных |
Метрика, нейронная сеть, машинное обучение, профайлинг, сегментация, статистика, сжатие данных |
В таблицах 2 и 3 приведены результаты расчетов матриц близостей дидактических единиц и мер ассоциаций.
Таблица 2
Матрица близости дидактических единиц
|
|
EL01 |
EL02 |
EL03 |
EL04 |
EL05 |
|
EL01 |
1 |
0 |
0 |
0,05 |
0,2 |
|
EL02 |
0 |
1 |
0,44 |
0,78 |
0 |
|
EL03 |
0 |
0,57 |
1 |
0,57 |
0 |
|
EL04 |
0,07 |
0,47 |
0,27 |
1 |
0 |
|
EL05 |
0,57 |
0 |
0 |
0 |
1 |
Таблица 3
Матрица мер ассоциаций
|
|
EL01 |
EL02 |
EL03 |
EL04 |
|
EL02 |
0 |
|
|
|
|
EL03 |
0 |
0,62 |
|
|
|
EL04 |
0,06 |
0,88 |
0,73 |
|
|
EL05 |
0,3 |
0 |
0 |
0 |
Проанализируем эти результаты. Учебный элемент EL01 не имеет пересечений с элементами EL02 и EL03 и незначительное пересечение с элементом EL04 (r14 = 0,05) . Но с элементом EL05 этот коэффициент уже существенен: r15 = 0,2. Связь этих элементов подтверждает и мера близости ассоциаций: S15 = 0,3.Поскольку r51 = 0,57 >r15, то элемент EL01 является базовым и должен изучаться первым, а элемент EL05 развивает и детализирует содержание первого элемента. Еще более тесной является связь между вторым и четвертым учебными элементами. Аналогичный анализ соответствующих коэффициентов матриц близости элементов и мер ассоциаций указывает, что элемент EL04 должен изучаться первым. Что касается, например, учебных элементов EL01иEL03 илиEL02 иEL05, то эти элементы могут изучаться независимо друг от друга.
В заключение отметим, что для нахождения ассоциаций и построения правильной последовательности изучения учебных элементов для многосеместровых курсов, содержащих большое число элементов, можно использовать пакеты прикладных программ, предназначенных для анализа больших массивов данных. Например, в пакете DeductorAcademicимеются готовые инструменты под названием «Ассоциативные правила» и «Деревья решений». И хотя эти инструменты предназначены, прежде всего, для выявления бизнес-правил при анализе транзакций в больших супермаркетах, нетрудно приспособить их и для описанных выше задач. Для сравнительно небольших по объему дисциплин достаточно использовать электронные таблицы Exсel.
Рецензенты:
Прохоров С.А., д.т.н., профессор, зав. кафедрой информационных систем и технологий ФГБОУ ВПО Самарского аэрокосмического им. академика С.П. Королева – Национального исследовательского университета, г. Самара;
Хаймович И.Н., д.т.н., кафедры информационных систем и компьютерных технологий ЧОУ ВО «Международный институт рынка», г. Самара.



