Характеристики, вид, распределение локальных максимумов для речевых фрагментов и для фрагментов пауз существенно различаются. Эти отличия проявляются в амплитудно-частотных соотношениях между локальными экстремумами (максимумами).
Объектом исследования является речевой сигнал на фоне слабого шума, длительность речевого сигнала составляет 4 с. Для вычисления вейвлет-спектра речевого сигнала используется формула непрерывного вейвлет-преобразования.
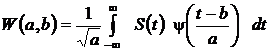 .
.
Для вычисления Фурье-спектра сегментов вейвлет-спектра используется преобразование Фурье:
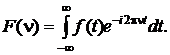
Для вычисления энергии сегментов фонем используется формула Парсеваля:
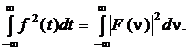
Для исследования зависимости энергии сегментов вейвлет-спектра от масштабного коэффициента a вычисляется энергия сегментов функций W(а,b). Математической моделью речевого сигнала в сегменте является:
![]() , (1)
, (1)
![]() . (2)
. (2)
Подставляя вместо вейвлет-спектра результат обратного Фурье-преобразования комплексно сопряженного спектра речевого сигнала и вейвлета, получаем:
![]() ,
,
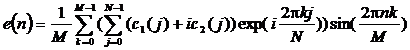 .
.
По формуле:
![]() (3)
(3)
вычисляется Фурье-спектр функций W(1,b), W(2,b). Энергия сегментов для каждого масштабного коэффициента а вычисляется по формуле:
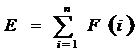 .
.
Таким образом, математической моделью речевого сигнала при выделении согласных фонем является энергия сегментов вейвлет-спектра речевого сигнала для разных масштабов. На рисунке 1 представлены графики зависимости энергии сегментов Е от масштабного коэффициента а вейвлет-преобразования W(а,b) слова часы. На рисунке 1 а масштабный коэффициент а меняется от 1 до 50 с шагом 1. При вычислении энергии просуммирована первая половина коэффициентов Фурье. На рисунке 1 б масштабный коэффициент а меняется от 0,4 до 2,9 с шагом 0,05. При вычислении энергии просуммирована вторая половина коэффициентов Фурье. На первом графике (рис. 1 а) видно, в каких сегментах выделяются гласные звуки а, ы. Фонемы ч, с не выделяются. На втором графике (рис. 1 б) фонемы ч и с (сегменты 4–13 и 32–38) хорошо видны и имеют энергию большую, чем гласные фонемы.
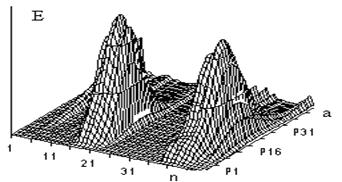
а
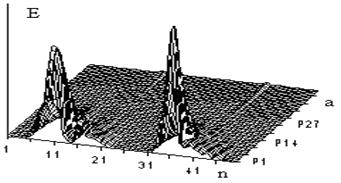
б
Рис. 1. Энергия сегментов ВП W(а,b) слова часы
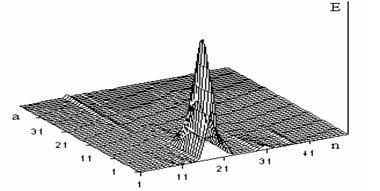
На рисунке 2 представлены графики зависимости энергии сегментов Е от масштабного коэффициента а ВП W(а,b) слова пуск. Параметры преобразования такие же, как для слова часы. Фонема п выделяется в сегментах 7–9. Фонема с выделяется (сегменты 15–21) так же, как выделяется фонема с в слове часы при небольших значениях масштабного коэффициента а. На графике хорошо видна пауза перед фонемой к.
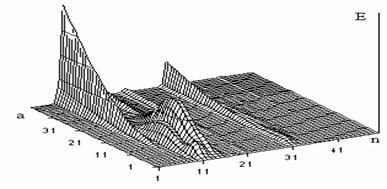
а
б
Рис. 2. Энергия сегментов ВП W(а,b) слова пуск
Вейвлет-анализ речевого сигнала показывает, что гласные фонемы и фонемы н, м, л имеют максимальные энергии при средних значениях а. Энергия фонем н, м, л много меньше энергии гласных звуков речи, но значительно выше энергии шума. Фонемы к, т, п, д выделяются при больших значениях а. Перед фонемами к, т имеется пауза. Такая закономерность наблюдается при многократном повторении и не зависит от случайных факторов. Шипящие и свистящие фонемы при малых значениях масштабного коэффициента а имеют энергию W(а,b), сравнимую с энергией гласных фонем. При средних значениях а они имеют энергию на уровне шума.
Можно заметить, что фонемы имеют отличающуюся друг от друга зависимость энергии W(а,b) от масштабного коэффициента а при использовании различного диапазона частот. На рисунках 3, 4 представлены графики зависимости энергии сегментов Е от масштабного коэффициента а ВП W(а,b) слова стоп. На рисунке 3 масштабный коэффициент а меняется от 1 до 50 с шагом 1.
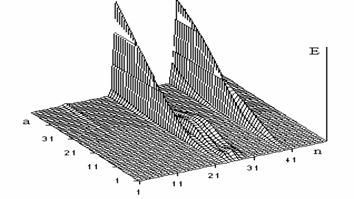
Рис. 3. Энергия сегментов ВП W(а,b) слова стоп для больших и средних значений масштабного коэффициента а
На рисунке 4 масштабный коэффициент а меняется от 0,4 до 2,9 с шагом 0,05.
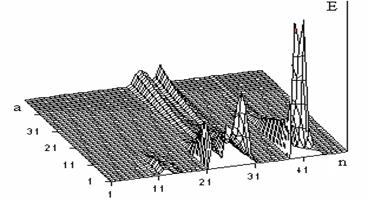
Рис. 4. Энергия сегментов ВП W(а,b) слова стоп для малых значений масштабного коэффициента а
На рисунках 2, 3 и 4 местоположение фонем п, т, к при больших значениях масштабного коэффициента а для слов пуск и стоп различное, как и для гласных фонем при средних значениях масштабного коэффициента а.
Например, слова выключить и отключить имеют одинаковые функции W4(4,b). Первое слово начинается с согласной, а второе – с гласной фонемы. Но отношение энергии сегментов ВП W(9,b) к энергии сегментов ВП W(2,b) первого слова больше, чем для второго в начале слова, так как для всех согласных фонем наблюдается такая закономерность. Для слова выключить пик в начале слова появляется, а для слова отключить – отсутствует.
На рисунке 5 представлена зависимость энергии сегментов ВП W(а,b) для масштабных коэффициентов а = 23 и а = 47. На графике отчетливо выделяется фонема н при большом масштабном коэффициенте а = 47, а фонемы а, е имеют незначительную энергию. Также на графике видна пауза между слогами лен и та, сегменты которой имеют энергию, незначительную для масштабных коэффициентов а = 23 и а = 47. Энергия сегментов ВП W(а,b) меняется при переходе от фонемы л к фонеме е и от фонемы е к фонеме н.
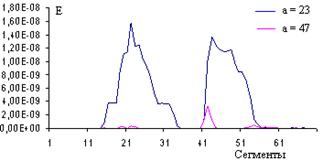
Рис. 5. Энергия сегментов слова лента для масштабных коэффициентов а = 23 и а = 47
Вейвлет-спектр W4(4,b) отчетливо выделяет границы между фонемами л, е, н и является основой для построения матрицы слова лента. В зависимости от количества максимумов этой функции прямоугольная поверхность (сегменты, масштабный множитель) разбивается на несколько областей. На рисунке 6 приведена проекция энергии сегментов ВП W(a,b) слова умножить на эту поверхность.
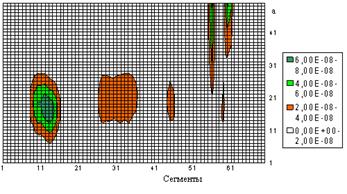
Рис. 6. Проекция энергии сегментов ВП W(a,b) слова умножить на прямоугольную поверхность (сегменты, масштабный множитель)
Для слова умножить функция W4(4,b) имеет 4 максимума, соответствующих фонемам у, о, и. Многомасштабный анализ, основанный на ВП, позволяет объединять слова в разные группы. В результате уменьшается время распознавания и увеличивается точность распознавания, так как базу данных слов можно разбить на подгруппы и представить в виде дерева поиска.
Таким образом, расположение фонем в слове или предложении можно установить, исследуя зависимость энергии сегментов вейвлет-спектра от масштабного коэффициента a. Для вычисления вейвлет-спектра речевого сигнала используется формула непрерывного вейвлет-преобразования. Вейвлет-анализ речевого сигнала показывает, что гласные фонемы имеют максимальные энергии при средних значениях масштабного коэффициента. Такая закономерность наблюдается при многократном повторении и не зависит от случайных факторов.
Работа выполнена при поддержке РФФИ, проект № 14-07-00143 а.
Рецензенты:Пряников В.С., д.т.н., профессор, профессор кафедры радиотехники и радиотехнических систем ФГБОУ ВПО «Чувашский государственный университет имени И.Н. Ульянова», г.Чебоксары;
Славутский Л.А., д.ф.-м.н., профессор кафедры автоматики и управления в технических системах ФГБОУ ВПО «ЧГУ им. И.Н. Ульянова», г. Чебоксары.



