Одним из таких процессов является перераспределение дохода потребителя между товарами различных категорий, описываемое с помощью функций спроса. С их помощью оказывается возможным проследить связь между изменением систем цен и доходов групп потребителей, с одной стороны, и спросом этих групп на товары и услуги, — с другой, решив таким способом задачу оптимального выбора потребителя. По этой причине удобное с точки зрения прикладной математики описание этих функций позволяет значительно упростить конструируемые с их помощью математические модели.
Постановка задачи
Как известно, для изучения изменения спроса в зависимости от дохода различных потребительских групп применяются в основном модели двух типов [3], [5].
1. Модель степенного ряда (функция Энгеля [2])
где α < 1 для спроса на предметы первой необходимости (1-й категории); α = 1 для спроса на товары длительного пользования (2-й категории); α > 1 для спроса на товары роскоши (3-й категории).
2. Функции Торнквиста
Здесь D1(I), D2(I), D3(I) определяют соответственно зависимости спроса от дохода на предметы первой необходимости, товары длительного пользования и товары роскоши соответственно.
Однако при таких представлениях возникает проблема согласования этих зависимостей, т. е. гладкого (с сохранением непрерывности первой и второй производной) перехода с одной зависимости на другую при непрерывном росте дохода.
В настоящей статье предложен способ, позволяющий получить аналитические зависимости для всех трех функций D1(I), D2(I), D3(I) с сохранением непрерывности их первых и вторых производных. Это позволяет применять при решении различного рода экономических задач богатый инструментарий методов математического анализа.
Описание метода
2.1. Для функции D1(I) справедливо следующее дифференциальное соотношение:
которое показывает, что убывание скорости спроса на товары первой необходимости должно быть пропорционально некоему предельному значению спроса D1max, после достижения которого потребность в товарах этой категории можно считать в первом приближении удовлетворенной. При этом величина D1max может быть получена путем статистического опроса населения (об исследованиях в данном направлении см. [2], [4]).
Тогда, решая это дифференциальное уравнение, получим:
При выборе константы C учтем, что рост спроса не должен превышать роста доходов, поэтому для величины скорости роста спроса должно выполняться соотношение: dD1(0)/dt =1, поэтому получим:
Окончательно, для функции D1(I) получим:
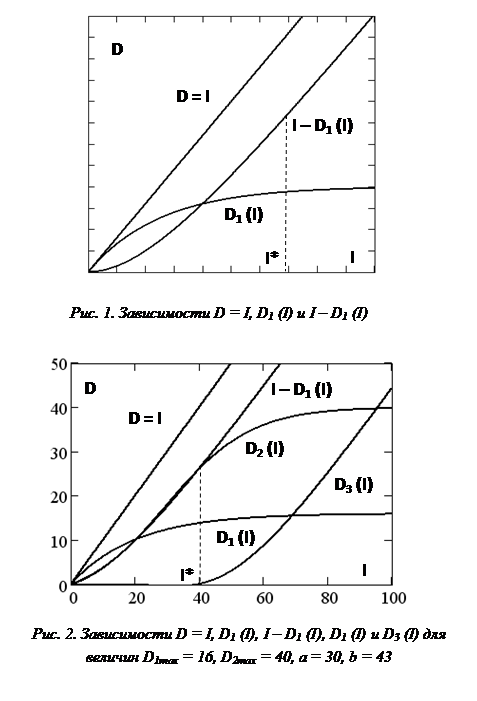
Как показывает рисунок 1, данная зависимость вполне адекватно отображает свойства функции спроса на товары первой необходимости.
2.2. Для дальнейшего построения модели примем положение о том, что с началом насыщения функции D1(I) вся оставшаяся часть доходов будет вначале расходоваться потребителем только лишь на потребление товаров 2-й категории, и только лишь потом, когда функция D2(I), перейдет в насыщение, часть доходов начнет поступать на приобретение товаров роскоши.
В этом случае для получения функции D2(I) следует вначале проанализировать следующую зависимость:
Эта зависимость, начиная с некоторой точки I*, должна переходить в насыщение, подобно полученной ранее функции D1(I) (см. рис. 1). Функция с подобным характером роста известна из физики и в приложении к исследуемому процессу выглядит так:
Определим константы A, B и b исходя из исследуемой модели.
Очевидно, что D2(0)=0, поэтому получим соотношение:
Кроме того, согласно модели:
поэтому
Значит,
Подставив (2.5) – (2.7) в (2.4), получим:
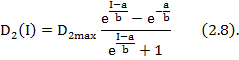
Константы a и b могут быть подобраны с помощью какого-либо математического программного пакета так, чтобы величина ошибки на промежутке от 0 до I* была наименьшей. В настоящей статье они подбирались в программной среде MathCad.
На рисунке 2 представлены результаты такого приближения для величин D1max = 16, D2max = 40, a = 30, b = 43. Как видно из рисунка 2, функциональная зависимость, показывающая весь оставшийся доход, непротиворечиво описывает зависимость D3(I) – зависимость спроса на товары роскоши от общего дохода. Согласно рассматриваемой модели для D3 (I) получим:
Из общих соображений понятно, что при неограниченном возрастании общего дохода (т. е. при условии I→∞), функция D3 (I) будет стремиться к I, причем никогда не достигнет этой величины. Такой характер поведения вполне согласуется с ее представлениями кривыми Торнквиста.
Математически получим:
В таблице 1 представлены подобранные программными методами пары коэффициентов a и b для некоторых наборов величин D1max и D2max. Для всех рассмотренных случаев величина ошибки δ(I) = I – D1 (I) – D2 (I) достаточно мала во всем интервале величин I от 0 до I*.
Таблица 1
Рассчитанные программным способом пары коэффициентов a и b для некоторых пар значений D1max и D2max
|
|
|||||
|
D1max |
D2max |
||||
|
30 |
35 |
40 |
45 |
50 |
|
|
14 |
a = 26 b = 35 |
a = 29 b = 39 |
a = 31,5 b = 43 |
a = 34 b = 47 |
a = 36 b = 50 |
|
16 |
a = 27,5 b = 37 |
a = 30 b = 41 |
a = 33 b = 45 |
a = 35,5 b = 48 |
a = 38 b = 52 |
|
18 |
a = 28 b = 38 |
a = 31 b = 42 |
a = 34 b = 46 |
a = 37 b = 50 |
a = 39 b = 54 |
|
20 |
a = 30 b = 40 |
a = 33 b = 44 |
a = 36 b = 48 |
a = 38 b = 51 |
a = 41 b = 55 |
Возможности применения метода
Приведенная ниже аппроксимация может быть использована для анализа распределения доходов между тремя основными группами товаров для различных групп потребителей. Ее достоинством является возможность представления зависимостей Dk (I), k = 1, 2, 3 в аналитическом виде, гладкими кривыми, что в свою очередь позволяет рассматривать широкий спектр задач прикладной экономики.
Так, например, представляется интересным исследовать динамику роста спроса на товары различных категорий с точки зрения функции полезности, которая, как известно, может быть представлена следующим образом:
Очевидно, что параметры α, β, и γ будут изменяться в зависимости от общего дохода I таким образом, что функция полезности всегда оставалась максимальной. Отметим также, что величины D1, D2, D3 также будут являться функциями от I согласно построенной модели.
Поскольку
при любой величине I потребитель пытается оптимизировать
свой доход с целью приобретения товаров всех категорий с наибольшей полезностью
для себя, то производная функции полезности 
будет
обращаться в ноль на всей траектории изменения коэффициентов α, β, и
γ. Поиск решения в общем виде представляется весьма непростой задачей,
поэтому будем искать ее решение на отдельных участках.
Пусть I < I*, тогда приближенно можно считать, что
Для функции полезности в любой оптимальной точке (D1;D2) имеем:
Учтем
тот факт, что D1 + D2 = I = const, и, значит, 
(оптимальное
решение выбирается при некоем фиксированном доходе), тогда
Если при этом учесть, что в предположении γ = 0, α + β = 1, то получим выражения для отыскания значений искомых коэффициентов для любых значений D1 и D2:
и, окончательно:
Далее, пусть I > I*; пренебрегая влиянием на функцию полезности величины спроса D1, получим:
Аналогично полученному ранее запишем:
Величину
на
этом участке можно с некоторым приближением рассчитывать исходя из условия:
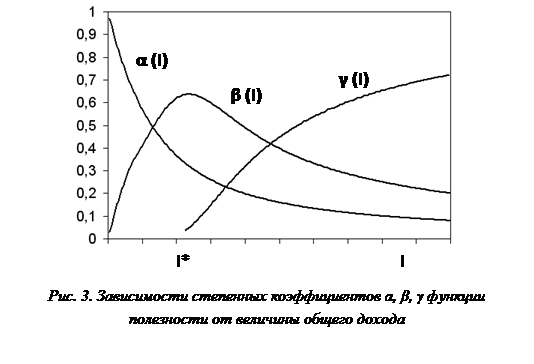
Произведенные таким образом расчеты представлены на рисунке 3 в виде зависимостей α(I), β(I), γ(I). Благодаря гладкому характеру функций Dk(I), k = 1, 2, 3 все эти зависимости также имеют гладкий характер. Кроме того, их динамика хорошо описывает процессы насыщения спроса товара k-й группы с последующим роста спроса на товар (k + 1)-й группы.
 |
Следует также отметить некоторые проблемные моменты вышеописанной модели, которые являются, однако, вполне устранимыми, а потому могут быть отнесены к ее «техническим» недостаткам.
1. Функция D1(I) задана только лишь параметром D1max, что не позволяет управлять ее начальным участком, когда весь доход идет только лишь на потребление товаров 1-й категории. Для устранения этого недостатка следует либо несколько усложнить вид этой функции, введя в нее новые параметры, либо положить ее равной величине I на этом участке.
2. При значительном увеличении дохода (I→∞), функция D1(I) асимптотически приближается к величине D1max, что, строго говоря, не соответствует действительности, поскольку спрос на товары 1-й категории все-таки продолжает расти, хотя и с небольшой скоростью. В этом случае представляется возможным описание функции D1(I) в виде:
где p — специально подобранный параметр, настолько малый, что действие его начинает сказываться лишь при достаточно больших величинах I. Сказанное можно отнести также к начальному участку функции D2(I).
3. Функция D2(I) на начальном участке своей зависимости имеет некоторое расхождение с функцией I – D1(I), что может привести к неприятным «скачкам» в прикладных расчетах. В этом случае ее можно заменить на этом участке самой функцией I – D1(I), имеющей гладкую форму.
Рецензенты:Анесянц С.А., д.э.н., профессор, руководитель Центра исследования рынка ценных бумаг института управления, бизнеса и права, г. Ростов-на-Дону;
Белоусов В.М., д.э.н., профессор кафедры «Экономическая социология и региональное управление» Института социологии и регионоведения Южного Федерального университета, г. Ростов-на-Дону.