Все оборудование (первичные двигатели, генераторы, трансформаторы, линии электропередачи, разнообразные электропотребители и множество другого основного и вспомогательного оборудования) электроэнергетических систем (ЭЭС) связано между собой в процессе производства, транспортировки, распределения и потребления электрической энергии.
Поскольку подавляющее большинство этого оборудования представляет собой динамические элементы, к тому же преимущественно нелинейные и с весьма значительным диапазоном постоянных времени, любая современная ЭЭС образует большую, многопараметрическую, жесткую, нелинейную, динамическую систему. В связи с этим полное и достоверное моделирование процессов, протекающих в оборудовании и ЭЭС в целом, представляет собой крайне сложную задачу. При этом в большинстве работ, посвященных её решению, основное внимание уделяется моделированию силового оборудования ЭЭС, а устройства релейной защиты (РЗ) моделируются упрощено. В то же время характер переходных процессов при различных возмущениях в реальной энергосистеме часто зависит от момента срабатывания устройств РЗ и действия противоаварийной автоматики. Это в том числе относится и к электромеханическим переходным процессам, продолжительность и характер которых определяет последующий режим работы и устойчивость энергосистемы.
Вышесказанное связано с тем, что в настоящее время для математического моделирования режимов и процессов в оборудовании и ЭЭС в целом преимущественно применяются программные и программно-технические комплексы, в которых для расчета системы дифференциальных уравнений используются численные методы. Численное моделирование, ввиду адекватности своей методической и инструментальной основы статическим задачам, обеспечивает успешный и эффективный расчет установившихся режимов ЭЭС. Однако моделирование переходных процессов ЭЭС с применением численных методов связано с совершенно иной, принципиально противоположной ситуацией, порождающей необходимость глубокой декомпозиции процессов и упрощения математической модели ЭЭС, а также существенных ограничений жесткости, дифференциального порядка этих моделей и длительности воспроизводимых процессов [2, 3, 6, 10, 11]. Причем, как показывает история развития программных средств данной специализации, указанная ситуация весьма слабо зависит от существующего развития методической и инструментальной основы цифрового моделирования. Причиной этого является наличие ограничительных условий численных методов [2, 3, 6, 10, 11]: решения дифференциального уравнения должны удовлетворять условию Липшица, длина интервала решения ограничивается по условию теоремы Далквиста и др.
Разработанный в Энергетическом институте Томского политехнического университета Всережимный моделирующий комплекс реального времени ЭЭС (ВМК РВ ЭЭС) «освобожден» от обозначенных выше ограничений.
Целью исследований является повышение адекватности моделирования переходных процессов в ЭЭС за счет использования всережимных математических моделей, учитывающих конкретные реализации и процессы в измерительных трансформаторах (ИТ).
Материалы и методы
ВМК РВ ЭЭС [4, 5] представляет собой параллельную, многопроцессорную, программно-техническую систему реального времени гибридного типа. Он объединяет в себе адаптируемую совокупность специализированных гибридных процессоров (СГП) всех элементов моделируемой схемы ЭЭС и информационно-управляющую систему.
Заложенные в ВМК РВ ЭЭС принципы построения исключают методическую ошибку решения математических моделей элементов и соответственно совокупной модели ЭЭС в целом, безотносительно к дифференциальному порядку, жёсткости и интервалу решения. Поэтому, точность решения гарантирована и определяется только инструментальной погрешностью аппаратной части комплекса, минимизация которой обеспечивается применением прецизионных интегральных компонентов.
Уникальные характеристики ВМК РВ ЭЭС стали доступны благодаря использованию концепции гибридного моделирования [7], которая для достижения высокой адекватности моделирования объединяются несколько методов: аналоговое, цифровое (численное) и физическое. Аналоговая часть обеспечивает отсутствие методической погрешности интегрирования. Цифровая часть позволяет на программном уровне реализовать алгоритмы управления и изменения параметров воспроизводимой системы. На физическом уровне обеспечивается связь и коммутация моделируемых элементов аналогично тому, как это осуществляется в реальной энергосистеме.
Свойства и возможности ВМК РВ ЭЭС позволяют интегрировать в комплекс (как на уровне Сервера, так и в микроконтроллеры СГП) математические модели релейной защиты и автоматики, учитывающие все ключевые программно-аппаратные особенности реализации конкретных устройств, а также процессы в измерительных трансформаторах тока и напряжения – детализированные модели [1, 8, 9]. Объем данной статьи не позволяет привести всю информацию по данной теме, поэтому ниже приведены фрагменты результатов моделирования наиболее распространенной в отечественной электроэнергетике электромеханической высокочастотной дифференциально-фазной защиты (ВЧДФЗ) – ДФЗ-201.
Фрагмент (схема замещения, граф, передаточная функция (ПФ) и дифференциальное уравнение на основе ПФ) математической модели для промежуточного трансформатора в составе блока реагирующих органов (пусковых и отключающих) ДФЗ-201 приведен ниже:
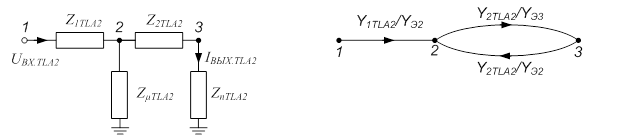
а) б)
Рис. 1. Схема замещения (а) и граф (б) промежуточного трансформатора
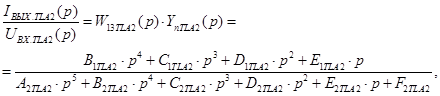
где B1TlA2, C1TLA2 и др. – коэффициенты, определяемые RLC-параметрами схемы промежуточного трансформатора ДФЗ.
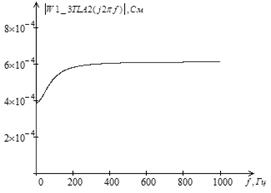
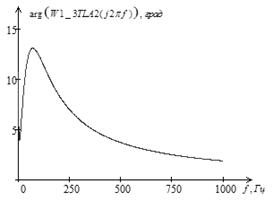
а) б)
Рис. 2. Амплитудно-частотная (а) и фазо-частотная (б) характеристики промежуточного трансформатора
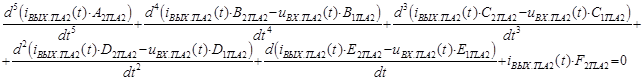
Реализация синтезированных математических моделей ДФЗ осуществляется путем трансформации математических моделей, представленных в виде системы дифференциальных уравнений, в программные коды, интегрируемые в программное обеспечение ВМК РВ ЭЭС.
Следующий раздел экспериментально подтверждает актуальность и необходимость использования детализированных математических моделей.
Результаты исследований и обсуждение
Исследования проведены на ВМК РВ ЭЭС с помощью учебной модели энергосистемы, фрагмент однолинейной схемы которой представлен на рис. 3. На рис. 4 и 5 представлены осциллограммы фазных токов линий электропередачи 220 кВ ВЛ-207 и ВЛ-210 при логическом учете и соответственно детальном моделировании функционирования основной защиты ВЛ-207 – дифференциально-фазной высокочастотной защиты ДФЗ-201. Ход эксперимента следующий: при возникновении трехфазного короткого замыкания (КЗ) на линии ВЛ-207 происходит срабатывание РЗ, при этом на воздушной линии электропередачи напряжением 220 кВ ВЛ-210 возникают синхронные качания. В первом случае (рис. 4) функционирование ДФЗ-201 реализовано лишь логически, посредством учета времени срабатывания защиты (30 мс) и времени срабатывания выключателей (40 мс). При этом синхронные качания, возникшие на ВЛ-210, имеют максимальную амплитуду 859,4 А. В случае использования детализированной математической модели ДФЗ-201 при том же времени срабатывания выключателей (40 мс) время срабатывания ДФЗ-201 составило 58 мс, что привело к более длительному режиму существования КЗ, и, как следствие, послужило причиной возникновения более глубоких (максимальная амплитуда составила 1001 А) синхронных качаний на линии ВЛ-210 (рис. 5).
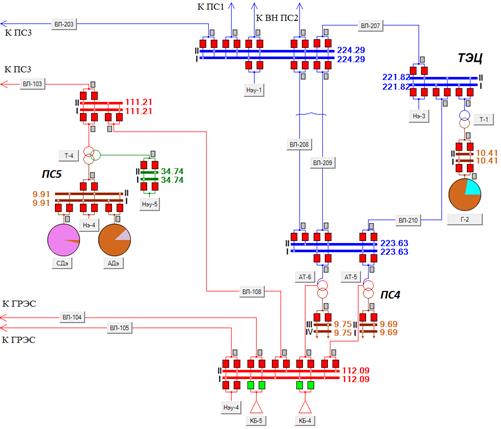
Рис. 3. Фрагмент моделируемой энергосистемы
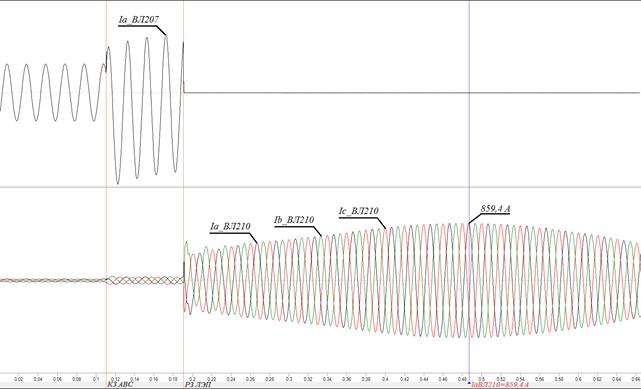
Рис. 4. Осциллограммы токов линий ВЛ-207 и ВЛ-210 при логическом учете функционирования РЗ ВЛ-207
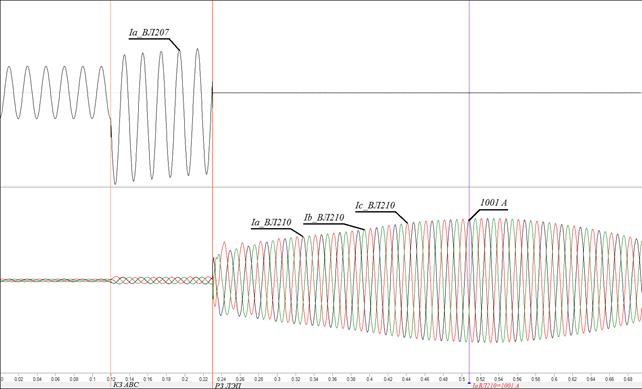
Рис. 5. Осциллограммы токов линий ВЛ-207 и ВЛ-210 при детальном моделировании функционирования РЗ ВЛ-207
Выводы
Результаты исследований, кратко обозначенные в данной статье, позволили сделать вывод о том, что характер протекания переходных процессов в значительной степени зависит от функционирования РЗ. При этом при использовании детализированных моделей защит и их упрощенных аналогов, реализующих лишь функцию сравнения контролируемых величин с уставкой и управление коммутационной аппаратурой, протекание переходного процесса в модели ЭЭС было различным.
Вышесказанное позволяет подтвердить тот факт, что при моделировании режимов и процессов в ЭЭС необходимо учитывать должным образом все влияющие на них в значительной степени элементы, к которым в частности относится и релейная защита ЭЭС.
Работа выполнена при поддержке мегагранта ТПУ № ВИУ_ЭНИН_138_2014 – «Гибридное моделирование и управление в интеллектуальных энергосистемах».
Рецензенты:
Гусев А.С., д.т.н., доцент, профессор кафедры электроэнергетических систем Энергетического института Национального исследовательского Томского политехнического университета, г. Томск;
Хрущев Ю.В., д.т.н., профессор, профессор кафедры электрических сетей и электротехники Энергетического института Национального исследовательского Томского политехнического университета, г. Томск.



