Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Проблема расчета расхода донных наносов в реках – одна из наиболее важных, сложных и до сих пор не решенных задач в теории руслового процесса. К настоящему времени создано несколько сотен формул, но на практике они дают результаты, отличающиеся друг от друга и данных наблюдений в десятки, сотни и более раз. Такое положение дел отрицательно сказывается на решении многочисленных инженерных задач на реках, требующих расчетов этой характеристики. Поэтому в Государственном гидрологическом институте (ГГИ) была предпринята попытка систематизировать имеющиеся формулы расчета расхода донных наносов и дать конкретные рекомендации по его расчету для различных природных условий. Общепринято, что удовлетворительной на сегодня можно считать точность расчета расхода донных наносов в 1,5–2 раза [4].

Причины неудовлетворительного состояния этого вопроса подробно рассмотрены в статье З.Д. Копалиани и А.А. Костюченко [7]. Основные из них: отсутствие однозначного определения понятия «донные наносы», отсутствие общепринятых методов разграничения влекомых, сальтирующих и взвешенных наносов, недостаточный учет специфики природных условий рек, в которых происходит транспорт донных наносов (их размера, уклона, гранулометрического состава, форм транспорта донных наносов), низкая точность зависимостей, используемых для расчетов сдвига частиц донных отложений, и пр.

Можно выделить четыре подхода к получению формул расхода донных наносов:

• универсальный подход (авторы подразумевают, что формула имеет неограниченное применение) – формулы И.И. Леви (1957) [3], Г.И. Шамова (1952) [14], Х.А. Эйнштейна (1950) [16];
• дифференцированный подход (каждому типу гидравлико-морфологических условий подбираются свои формулы);
• разработка региональных зависимостей (обобщения для рек определенного типа, региона, например для горных рек Средней Азии – формула Р.В. Тимировой и З.А. Классен (1970) [12] или формула В.В. Ромашина (1990) для рек Черноморского побережья Краснодарского края [13]);
• вывод локальных зависимостей – для конкретного участка определенной реки.

Время показало, что в силу сложности, многофакторности и слабой изученности процесса транспорта донных наносов универсальный подход пока не оправдывает своего назначения.

Дифференцированный подход, разрабатываемый в Отделе русловых процессов (ОРП) ГГИ, подразумевает разделение задачи расчета транспорта донных наносов в зависимости от природных условий на типы и подбор для каждого типа наиболее подходящих формул. В рамках дифференцированного подхода мы выделили следующие типы транспорта донных наносов:

• транспорт донных наносов на больших равнинных реках – в форме гряд;
• транспорт донных наносов на малых и средних равнинных реках – в форме гряд;
• грядовый транспорт на горно-предгорных реках;
• бесструктурный транспорт на горно-предгорных реках.

Особенности транспорта донных наносов на равнинных реках

Транспорт донных наносов на равнинных реках имеет свои особенности:

• движение наносов при установившемся движении воды происходит в форме гряд (соблюдается условие );
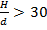• гранулометрический состав песчаных наносов относительно однороден, поэтому в качестве характерного часто используется средневзвешенный диаметр .

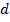Расход донных наносов на единицу ширины русла при грядовом перемещении наносов рассчитывается по следующей формуле:

– расход донных наносов на единицу ширины русла в рыхлом теле, м3/с/м,

α – коэффициент формы гряды, в среднем равный 0,6,

– высота гряды,

– скорость перемещения гряды.

Таким образом, располагая надежными формулами для расчета высоты гряд hг и скорости их движения Cг, можно рассчитать расход донных наносов при грядовой форме их перемещения [10, 11].

Особенности транспорта донных наносов на горно-предгорных реках

Транспорт наносов на горных реках отличается рядом особенностей:

• транспорт донных наносов имеет прерывистый характер и происходит лишь в периоды повышенной водности (половодья, паводка), а не в течение всего года, как на равнинных реках;
• гранулометрический состав донных наносов горных рек разнороден, поэтому частицы разных фракций донных отложений в зависимости от водности приходят в движение не одновременно.

Поэтому

• измерение расхода донных наносов на горной реке в межень не имеет смысла, а в многоводный период невозможно (скорости течения достигают 8 м/с, паводки труднопрогнозируемы, кратковременны и часто происходят в ночное время);
• наиболее надежный способ оценки транспорта наносов на горных реках сегодня – его физическое моделирование. Горный поток может быть воспроизведен в лаборатории без нарушения всех критериев его подобия, без искажения масштабов зернистой шероховатости.

На горных реках гряды формируются при следующих условиях [9]:

• при гранулометрическом составе, близком к однородному – случай срыва русловой отмостки (): , ;
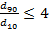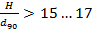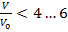• при разнородном гранулометрическом составе – , .

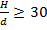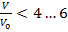Расчетные формулы

Все формулы для расхода донных наносов получены на основе некоторых теоретических соображений и эмпирических данных полевых или лабораторных (размываемых гидравлических моделей или лотков), хотя те из них, которые носят обобщающий характер, часто называются теоретическими.

Все известные формулы мы разбили на определенные типы.

• Формулы, полученные для грядового движения
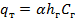  – 50 формул.

• Формулы, полученные без учета грядового движения донных наносов – 84 формулы.

- Основан на критерии начала движения. В качестве последнего используются:

1) критическая скорость потока – 18 формул;

2) критический расход воды – 7 формул;

3) критическое касательное напряжение на дне потока – 35 формул;

4) критический энергетический уклон – 1 формула.

- Вероятностный подход – 4 формулы.

- Регрессионные зависимости – 19 формул.

• Региональные зависимости .
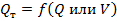• Локальные зависимости .

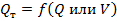Разработка локальных зависимостей требует нескольких лет наблюдений на речном участке и целесообразна при строительстве дорогостоящих гидротехнических сооружений типа плотин.

Эмпирический материал и методы исследования

Без учета региональных и локальных зависимостей нами были проверены 134 формулы для расхода донных наносов. Основой для сравнения послужил большой массив данных, полевых и лабораторных, собранных ОРП за многие годы. Массив данных состоит из трех блоков:

• по равнинным рекам: большим, малым и средним – данные полевых измерений (в основном данные ОРП);
• по грядовому транспорту на горно-предгорных реках – данные лабораторных лотков и гидравлических моделей (данные ОРП, советских и зарубежных авторов);
• по бесструктурному транспорту на горно-предгорных реках – данные лабораторных лотков (данные ОРП).

Формулы, полученные без учета гряд, проверялись на всем массиве данных, формулы для грядового движения – только для первых двух блоков.

Данные измерений по равнинным рекам

Основой для сравнения формул в рамках данного типа послужил массив данных, собранных ОРП в течение многих лет в рамках экспедиций на большие, малые и средние реки СССР [10, 11], а также данные японских авторов по р. Хии [19]. Массив данных состоит из 200 измерений. Все данные получены на единой методической основе методом повторного продольного эхолотирования речного русла. При этом данные измерений высоты и скорости перемещения гряд представляют собой не осредненные характеристики на участке эхолотирования, а данные по конкретным грядам установившегося профиля, геометрические (высота, длина) и динамические (скорость перемещения) характеристики которых в процессе производства измерений остаются постоянными. Гидравлические и морфометрические характеристики измерений приведены в таблице 1.

Таблица 1

Диапазон изменения гидравлических характеристик потока и песчаных гряд в использованных натурных исследованиях

Из таблицы следует, что равнинные реки спокойные (число Фруда значительно меньше единицы), размер наносов на малых реках больше, гряды на малых реках движутся значительно быстрее, гладкость потока велика.

Данные измерений по горно-предгорным рекам

Данные по грядовому транспорту

В качестве исходного материала для данного типа были взяты данные 6 лотковых экспериментов и 4 размываемых гидравлических моделей участков горно-предгорных рек (данные ОРП ГГИ [5], а также В.Н. Гончарова [2], В.Ф. Пушкарева [8], Г.П. Уильямса [20] и Х.П. Гая, Д.Б. Саймонса и И.В. Ричардсона [15]). Массив данных включал 220 измерений. В рассматриваемых экспериментах гранулометрический состав донных отложений был однородными (). Гидравлические и морфометрические характеристики измерений приведены в таблице 2.

Таблица 2

Диапазон изменения гидравлических характеристик потока и песчаных гряд в использованных лабораторных исследованиях

Сравнение относительных показателей таблиц 1 и 2 говорит, что горные потоки более бурные, гладкость потока ниже, относительная высота гряды примерно такая же, гряды горных потоков формировались значительно меньшим количеством частиц, чем на равнинных реках.

Данные по бесструктурному транспорту

Исходным материалом послужили данные трех серий экспериментов, проведенных в Русловой лаборатории ГГИ (25 измерений расхода донных наносов). Прототипами для первых двух экспериментов послужили два участка р. Мзымты (Черноморское побережье Северного Кавказа) (8-метровый гидравлический лоток) [18], а для третьей серии экспериментов – участок русла р. Туапсе (100-метровый гидравлический лоток) [7].

Основные гидравлические характеристики экспериментов менялись в следующих пределах:

• первый эксперимент: ; ; ;
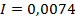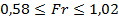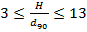• второй эксперимент: ; ; ;
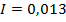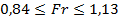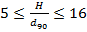• третий эксперимент: ; ; .

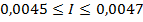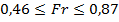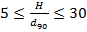Гранулометрический состав в первой и третьей сериях экспериментов был неоднородным, во второй серии — однородным.

Особенностью первых двух экспериментов явилось определение гранулометрического состава (грансостава) донных наносов на каждой стадии экспериментов (фазе моделируемого паводка). Это позволило проследить изменение грансостава наносов по ходу паводка и его отличие от исходного состава донных отложений. На рисунках 1 и 2 представлены кривые грансоставов донных наносов на каждой стадии паводка вместе с исходными кривыми донных отложений. Кривые второго эксперимента на всех стадиях очень близки к исходной, в первом эксперименте разброс значительно больший.

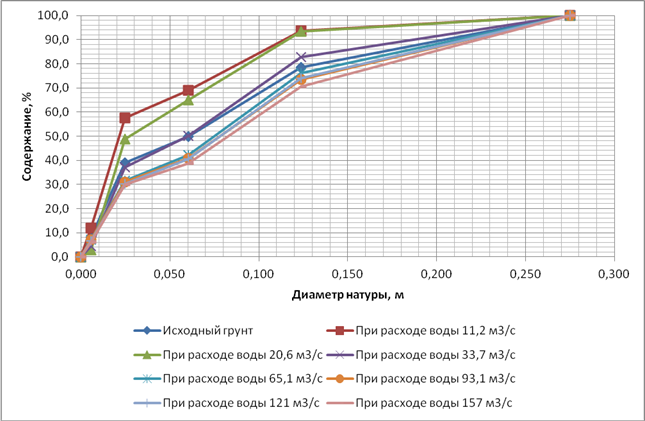
Рис.1. Интегральные кривые гранулометрического состава наносов на каждой стадии повадка первого эксперимента по сравнению с исходной кривой донных отложений

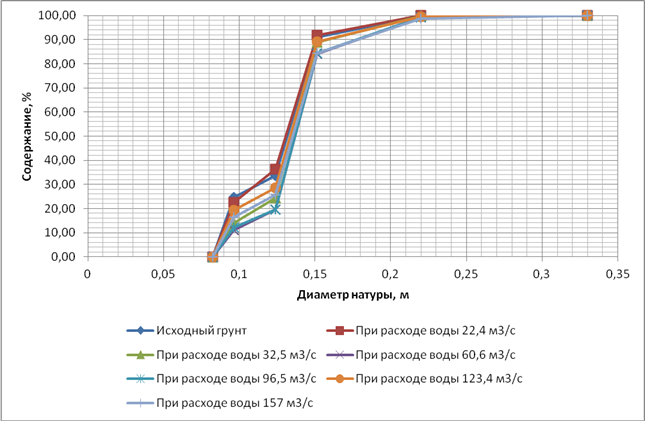
Рис. 2. Интегральные кривые гранулометрического состава наносов на каждой стадии повадка второго эксперимента по сравнению с исходной кривой донных отложений

В дальнейшем все формулы, имеющие в своем составе характеристику грансостава, для первых двух экспериментов проверялись с использованием грансостава донных отложений и грансостава донных наносов на соответствующей стадии паводка.

Выводы и рекомендации

Для оценки точности формул был выбран критерий , а допустимым интервалом ошибки – диапазон , т.е. занижение и завышение результата в два раза.

Анализ результатов расчетов по формулам позволил обосновать следующие рекомендации по расчетам расхода донных наносов в реках.

1. Для больших равнинных рек рекомендовано 9 формул, учитывающих грядовое движение, и 9 формул, не учитывающих его:

o З.Д. Копалиани [17] – из числа формул первой группы, учитывающих грядовое движение

м, м/с (1)

– по В.Н. Гончарову.

o Л.Д. Когана и В.П. Углова (1985) [6] – из числа формул второй группы, не учитывающих грядовое движение

кг/с/м (2)

при ,

при ,

при

– по В.В. Романовскому.

2. Для малых и средних равнинных рек рекомендовано 11 формул, учитывающих грядовое движение, и 9 формул, не учитывающих его:

o Б.Ф. Снищенко и З.Д. Копалиани [17]

м, м, м/с (3)

o А.Н. Бутакова (1998) [1]

м3/c/м (4)

3. Для грядового движения на горно-предгорных реках рекомендовано 12 формул, учитывающих грядовое движение, и 6 формул, не учитывающих его:

o А.А. Костюченко и З.Д. Копалиани [17]

м, м/с (5)

– по В.Н. Гончарову.

o В.Н. Лазарев, Ф.М. Чернышов (1974) [9]

м3/с/м (6)

4. Для бесструктурного транспорта на горно-предгорных реках рекомендовано всего 3 формулы:

o Л.Г. Гвелесиани (1946) [18]

кг/c/м (7)

м/с

o И.И. Леви (1957) [18]

м3/с/м (8)

для квадратичной области (, 1…1,5 мм):

м/с

м/с

o формула Г.И. Шамова (1952) [18]

кг/с/м (9)

м/с.

Зависимости (1)-(9) позволяют рассчитывать расход донных наносов в реках дифференцированно: для больших, средних и малых равнинных и горно-предгорных участков рек при структурной (грядовой) и бесструктурной (безгрядовой) формах движения донных наносов.

Рецензенты:

Боровков В.С., д.т.н., профессор, профессор кафедры гидравлики и водных ресурсов ФБГОУ ВПО «Московский государственный строительный университет Минобрнауки РФ», г. Москва;

Дебольский В.К., д.т.н., профессор, заведующий лабораторией динамики русловых потоков и ледотермики ФГБУН «Институт водных проблем Российской академии наук», г. Москва.