При получении положительной предварительной оценки инвестиционно-инновационного проекта, реализуемого строительным предприятием, на основе метода экспертных опросов переходят к более детальным расчётам эффективности этого проекта. За время реализации проекта могут измениться стадии жизненного цикла инновационной продукции, характеристики спроса на неё, а также объёмы затрат и доходов. Это означает варьируемость экономических параметров жизненного цикла проекта во времени. В соответствии с методикой агрегированных жизненных циклов рыночный спрос дифференцируется по формам образования относительно той или иной стадии цикла продукта (потенциальный спрос – стадия исследований и разработок; формирующийся спрос – стадия внедрения; развивающийся спрос – стадия роста; сформировавшийся спрос – стадия зрелости; затухающий спрос – стадия спада). Каждая стадия жизненного цикла характеризуется определёнными значениями объёмов реализации инновационной продукции. Таким образом, можно определить экономические параметры той или иной стадии жизненного цикла проекта на необходимом промежутке времени, исходя из тенденций развития рынка, и выбрать нужную функцию Y(t) для прогнозирования перспективных изменений [2].
Цель исследования заключается в определении возможностей применения методов экстраполяции и, в частности, аналитического выравнивания, а также экономико-математического моделирования при построении прогнозов финансовой реализуемости и эффективности инвестиционно-инновационных строительных проектов.
Материал и методы исследования
Следующим этапом в осуществлении инвестиционно-инновационного проекта является получение трендовых моделей экстраполяции интересующих показателей. Таким показателем может быть, например, объём дохода от реализации проекта. Экстраполяция служит одним из наиболее распространенных методов прогнозирования, предполагающим продление прошлых тенденций развития явления (трендов) на будущее. При этом исходят из следующих допущений: развитие процессов может быть охарактеризовано плавной траекторией трендов, а условия, определяющие прошлые тренды, не претерпят существенных изменений в перспективе [1]. В прогнозировании основных тенденций развития предприятия, с учётом изменения рыночных составляющих, может применяться метод аналитического выравнивания. Основным содержанием этого метода является расчёт тренда (Yt) как функции времени:
![]()
Это один из пассивных методов прогнозирования, основанный на инерционности развития явлений, т. е. проектировании прошлых тенденций в будущее, а также на независимости показателей развития от влияния тех или иных факторов [1]. Определение теоретических (расчётных) уровней ![]() производится на основе адекватной математической функции. Подбор функции осуществляется с помощью метода наименьших квадратов – минимальности отклонений суммы квадратов между теоретическими (
производится на основе адекватной математической функции. Подбор функции осуществляется с помощью метода наименьших квадратов – минимальности отклонений суммы квадратов между теоретическими (![]() ) и эмпирическими (Yi) уровнями:
) и эмпирическими (Yi) уровнями:
![]()
Данное уравнение принимается в качестве критерия оценки соответствия теоретических и фактических уровней ряда динамики. Если выбранный тип математической функции адекватен основной тенденции развития изучаемого явления во времени, то синтезированная на этой основе трендовая модель может применяться в прогнозировании. Практика выявления тренда в динамических рядах показывает, что порой затруднительно определить тип развития рядов только с помощью абсолютных приростов, темпов роста и прироста. Показатели, точно соответствующие признакам эталонных математических функций, являются скорее исключением, чем правилом. Совокупное действие различных факторов обуславливает изменения показателей динамических рядов, не согласующиеся с основными признаками типовых функций. Это осложняет выбор адекватной математической функции для аналитического выравнивания. В лучшем случае на основе качественного анализа тренда может быть выдвинута рабочая гипотеза возможных типов развития. Для её подтверждения можно использовать графический метод: наглядное изображение анализируемого ряда динамики позволяет получить образное представление о размещении эмпирических уровней [4].
Одним из показателей адекватности математической функции является стандартизированная ошибка аппроксимации (![]() ):
):
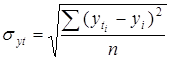
За более адекватную принимается функция, имеющая минимальную ![]() .
.
Для определения параметров (а0, а1, а2, а3) математических функций используется способ отсчёта времени от условного начала [2]. Он основан на обозначении в ряду динамики показаний времени таким образом, чтобы ![]() .
.
При этом в ряду с нечётным числом уровней порядковый номер уровня, находящегося в середине ряда, обозначают через нулевое значение и принимают его за условное начало отсчёта времени с интервалом (+1) всех последующих уровней и с интервалом (-1) всех предыдущих уровней. При чётном числе уровней порядковые номера верхней половины ряда (от середины) обозначаются числами: -1, -3, -5, -7 и т.д., а нижней половины ряда обозначаются: +1, +3, +5, +7 и т.д.
С помощью перебора решений по намеченным математическим функциям (с учётом ![]() ) и проведения сравнительного анализа тренда выбирается наиболее адекватная математическая функция, которая затем используется в прогнозировании. На практике экстраполяция выполняется не точечными (дискретными), а интервальными оценками. Для определения границ интервалов используется формула:
) и проведения сравнительного анализа тренда выбирается наиболее адекватная математическая функция, которая затем используется в прогнозировании. На практике экстраполяция выполняется не точечными (дискретными), а интервальными оценками. Для определения границ интервалов используется формула:
![]() ,
,
где: ![]() – коэффициент доверия по распределению Стьюдента;
– коэффициент доверия по распределению Стьюдента;
![]() – остаточное среднее квадратическое отклонение тренда, скорректированное по числу степеней свободы.
– остаточное среднее квадратическое отклонение тренда, скорректированное по числу степеней свободы.
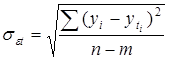 ,
,
где: n – число уровней базисного ряда динамики;
m – число параметров адекватной модели тренда.
При таком способе оценки результата экстраполяции получают определённую степень вероятности составленного прогноза (например, границы изменения объёма дохода при реализации инновационной продукции). Важно отметить, что экстраполяция носит условный характер. В краткосрочном прогнозировании экстраполяция прошлых усредненных показателей приводит к игнорированию необычных отклонений от основных тенденций. В долгосрочных же прогнозах используется слишком большое агрегирование, не учитывающее изменения в структуре и технологии производства, особенности развития рынков [1].
При разработке прогнозов необходимо привлечение дополнительной информации, на основе которой в полученные методом экстраполяции результаты вносятся соответствующие коррективы. Поэтому в дальнейшей оценке эффективности инвестиций для инновационных строительных проектов может быть использовано математическое моделирование, как один из сложных, нонаиболее точных методов прогнозирования.
Методы математического моделирования основаны на построении моделей типа: y = f(x), где y – результативный признак; x – факторный признак, влияющий на результативный [4]. Корреляционная связь является разновидностью факторной связи и представляет собой частичную зависимость результативного признака (y) от факторного признака (x). На (у) возможно также влияние прочих факторов (ε):
у = ψ(х) + ε
В корреляционных связях при одном и том же значении учтённого факторного признака возможны различные значения результативного признака, обусловленные влиянием разнородных по составу, направлению и силе воздействия прочих факторов. Влияние учтённых факторных признаков определяется способом научной абстракции от прочих факторов. При этом становится возможным установление закономерностей взаимодействия и получение количественных характеристик корреляционной связи.
В корреляционном анализе чаще всего применяемой является методология парной корреляции, рассматривающая влияние вариации факторного признака (х) на результативный признак (у). При изучении этой зависимости форма связи характеризуется функцией регрессии, описываемой уравнением прямолинейной или криволинейной связи [2]. Корреляционно-регрессионный анализ как один из методов математического моделирования позволяет получить более надёжное и достоверное прогнозное значение конечного результата.
Решение уравнений связи предполагает вычисление по исходным данным их параметров путем выравнивания по методу наименьших квадратов. Параметры уравнения регрессии определяются решением системы нормальных уравнений с использованием способа определителей. За счёт этого сводятся к минимуму неточности округлений в расчётах параметров. Вычисленные значения параметров необходимы для синтезирования математической модели зависимости (у) от (х). Проверка параметров синтезированной модели на типичность (при численности объектов анализа n< 30 единиц) осуществляется по фактическим значениям t-критерия Стьюдента:
![]()
![]()
где а0 и а1 – параметры уравнения регрессии;
![]() – среднее квадратическое отклонение результативного признака yi от выровненных значений
– среднее квадратическое отклонение результативного признака yi от выровненных значений ![]() ;
;
![]() – среднее квадратическое отклонение факторного признака xiот общей средней
– среднее квадратическое отклонение факторного признака xiот общей средней ![]() .
.
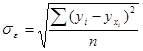
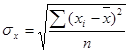
Фактические значения (![]() ) и (
) и (![]() ) сравниваются с критическим (tk) по таблице Стьюдента с учётом принятого уровня значимости (α) и числа степеней свободы (k). Полученные в анализе корреляционной связи параметры уравнения регрессии признаются типичными, если:
) сравниваются с критическим (tk) по таблице Стьюдента с учётом принятого уровня значимости (α) и числа степеней свободы (k). Полученные в анализе корреляционной связи параметры уравнения регрессии признаются типичными, если: ![]() >tk<
>tk<![]() [2]. Смысловое содержание синтезированной модели применительно к инвестиционно-инновационной деятельности состоит в том, что она может характеризовать, например, среднюю величину объёма дохода от реализации инновационного проекта (
[2]. Смысловое содержание синтезированной модели применительно к инвестиционно-инновационной деятельности состоит в том, что она может характеризовать, например, среднюю величину объёма дохода от реализации инновационного проекта (![]() ) в зависимости от вариации признака-фактора (х).
) в зависимости от вариации признака-фактора (х).
Следующим важным этапом корреляционного анализа связи является оценка практической значимости синтезированной модели. Здесь обосновывается применение метода функционального анализа при изучении корреляционной зависимости и возможность использования способа научной абстракции. Правомерность такого приёма анализа оправдана лишь в тех случаях, если корреляционная связь (у = ψ(х) + ε) незначительно отстоит от связи функциональной (y = f(x)) и даёт несущественные погрешности. Для оценки тесноты связи между признаками (х) и (у) используются:
а) общая дисперсия результативного признака (![]() ), отображающая совокупное влияние всех факторов:
), отображающая совокупное влияние всех факторов:
![]()
Отклонения ![]() обусловлены тем, что сочетание значений факторов, влияющих на вариацию признака (у), для каждой единицы анализа различно.
обусловлены тем, что сочетание значений факторов, влияющих на вариацию признака (у), для каждой единицы анализа различно.
б) факторная дисперсия результативного признака (![]() ), отображающая вариацию (у) только от воздействия изучаемого фактора (х):
), отображающая вариацию (у) только от воздействия изучаемого фактора (х):
![]()
Отклонения ![]() характеризуют колеблемость выровненных значений (ух) от их общей средней величины (
характеризуют колеблемость выровненных значений (ух) от их общей средней величины (![]() ).
).
в) остаточная дисперсия (![]() ), отображающая вариацию результативного признака (у) от всех прочих, кроме (х), факторов:
), отображающая вариацию результативного признака (у) от всех прочих, кроме (х), факторов:
![]()
Отклонения ![]() характеризуют колеблемость фактических значений результативного признака (у) от выровненных значений (
характеризуют колеблемость фактических значений результативного признака (у) от выровненных значений (![]() ).
).
При функциональной связи значения (ух) полностью совпадают с соответствующими индивидуальными значениями (yi) и в этом случае ![]() . При отсутствии связи вариация (xi) не отражается на изменении (
. При отсутствии связи вариация (xi) не отражается на изменении (![]() ) – в этом случае
) – в этом случае ![]() . При наличии корреляционной связи
. При наличии корреляционной связи ![]() <
<![]() [3]. Оценка практической значимости модели, синтезированной на основе уравнения криволинейной связи, производится посредством индекса корреляции (R):
[3]. Оценка практической значимости модели, синтезированной на основе уравнения криволинейной связи, производится посредством индекса корреляции (R):
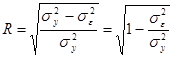
Для оценки практической значимости модели, синтезированной на основе уравнения прямолинейной связи, применяется линейный коэффициент корреляции (r):
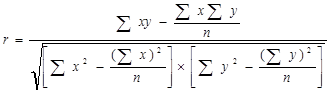
Величины (R) или (r) соотносятся со шкалой Чеддока, которая качественно характеризует тесноту связи (х) и (у). Значимость индекса корреляции (R)определяется по F-критерию Фишера:
![]() ,
,
где m – число параметров уравнения регрессии.
Величина (FR) сравнивается с критическим значением (Fk), определённым по таблице F-критерия с учётом принятого уровня значимости (α) и числа степеней свободы: k1 = m – 1 и k2 = n – m. Если FR>Fk, то величина (R) существенна. Оценка значимости коэффициента корреляции (r) производится по t-критерию Стьюдента:
![]()
Значение (tr) сравнивается с критическим значением (tk), определённым по таблице t-распределения Стьюдента с учётом заданного уровня значимости (α), и числа степеней свободы (k). Если tr>tk, то величина (r) существенна [3]. При значениях показателей тесноты связи, превышающих 0,7, зависимость результативного признака (у) от факторного (х), является высокой, а при значениях более 0,9 – весьма высокой. В соответствии с показателем индекса детерминации (R2) – это означает, что более половины общей вариации результативного признака (у) объясняется влиянием фактора (х). Следовательно, применение метода функционального анализа для изучения корреляционной связи оправдано, а синтезированные при этом математические модели пригодны для их практического использования.
Заключение
Обобщая вышеизложенное, следует отметить взаимосвязь этапов прогнозирования инвестиционно-инновационного развития строительных предприятий и показателей их эффективности [5]. Реализация инвестиционно-инновационных проектов, эффективность которых подтверждена специальными методами оценки и экспертно, экстраполяция объёма доходов на перспективу с учётом стадий жизненного цикла спроса на инновационную продукцию, моделирование результатов деятельности в зависимости от результативности реализуемых инвестиционно-инновационных проектов способствуют росту экономических показателей предприятий строительного комплекса.
Рецензенты:
Хрусталев Б. Б., д.э.н., профессор, заведующий кафедрой «Экономика, организация и управление производством» ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза;
Хаметов Т. И., д.э.н., профессор, заведующий кафедрой «Землеустройство и геодезия» ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза.



