Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Для решения двумерной задачи диффузии-конвекции,, была построена библиотека двухслойных итерационных методов, предназначенных для решения девятидиагональных сеточных уравнений. Данная библиотека решателей систем линейных алгебраических уравнений (СЛАУ) состоит из:

– метода Якоби [4];

– метода минимальных поправок;

– метода скорейшего спуска;

– метода Зейделя;

– метода верхней релаксации;

– адаптивного МПТМ вариационного типа [1; 2; 6].

Разработанная библиотека итерационных методов была протестирована на модельной задаче диффузии-конвекции-реакции [9; 11]. Задача решена на сетке размером 100×100, шаги по пространственным переменным равны 1 м, коэффициент турбулентного обмена μ=10 м2/с, скорость конвективного переноса равна нулю. Функция, описывающая распределение и интенсивность источников веществ, представлена точечным источником. Для решения модельной задачи использованы схемы с весами, при этом вес схемы задавался равным 0,5. Шаг по временной переменной менялся от 0,001 до 1000 с. Завершение работы решателей СЛАУ происходило при выполнении следующего условия: равномерная норма вектора невязки меньше заданного значения [3].

В таблице 1 приведены зависимости количества итераций, необходимых для решения модельной задачи, от шага по временной переменной.

Из приведенных в таблице значений количества итераций, необходимых для решения модельных задач диффузии-конвекции-реакции, видно, что чем больше шаг по временной переменной, тем больше итераций требуется для решения данной задачи. Это связано с тем, что при увеличении шага по временной переменной уменьшается диагональное преобладание, вследствие чего растет число обусловленности матрицы коэффициентов. Как показано выше, скорость сходимости напрямую зависит от числа обусловленности матрицы коэффициентов. С этим и связан рост числа итераций, необходимых для решения сеточных уравнений итерационными методами.

Таблица 1

Зависимости количества итераций решения сеточных уравнений итерационными методами от шага по временной переменной

Не трудно заметить, что МПТМ является наиболее эффективным из предложенных методов. При больших шагах по временной переменной МПТМ требуется наименьшее количество итераций, по сравнению с остальными методами. Достаточно эффективен и метод верхней релаксации, но при малых шагах по временной переменной его использовать не целесообразно. При решении сеточных уравнений методы Якоби, Зейделя и вариационного типа показали свою эффективность в узком диапазоне задаваемых параметров, однако использовать данные методы при решении плохо обусловленных задач не целесообразно.

Алгоритм параллельной реализации попеременно-треугольного метода

Схему итерационного двухслойного модифицированного попеременно-треугольного метода запишем в виде:

, ,

где xn – вектор решения; – вектор поправки; А – оператор сеточного уравнения; D – диагональная часть оператора A; w – итерационный параметр; R1, R2 – верхняя и нижняя треугольные части оператора A; – вектор невязки; f – правая часть сеточного уравнения.

Для параллельной реализации адаптивного МПТМ использованы методы декомпозиции области по одному направлению. Наиболее трудоемким расчетом с точки зрения построения параллельной программной реализации является расчет вектора поправки, который выполняется в два шага:

1) ,

2) .

На первом шаге рассчитываются элементы вспомогательного вектора снизу вверх, а затем, зная его, на втором шаге находятся элементы вектора поправки сверху вниз. Схемы расчета вспомогательного вектора и вектора поправки представлены на рис. 1 (стрелками показаны направления счета и передачи).

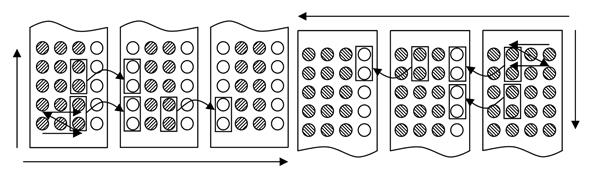
а) б)

Рис. 1. Схемы расчета вспомогательного вектора yn (а) и вектора поправки wn (б).

В схеме для расчета вектора только первый процессор не требует дополнительной информации и может независимо от других процессоров посчитать свою часть области, остальные процессоры ждут от предыдущего передачи элементов, стоящих в начале строки. Передача по одному элементу не оптимальна, так как появляются временные затраты, связанные с их организацией. Суммарное время на накладные расходы можно уменьшить путем увеличения объема передач. Данные рассуждения используются для расчета вектора поправки.

Результаты численных экспериментов

Для решения задачи транспорта МВС использован адаптивный модифицированный попеременно-треугольный метод (МПТМ) минимальных поправок. При параллельной реализации использованы методы декомпозиции сеточных областей для вычислительно трудоемких задач диффузии-конвекции, учитывающие архитектуру и параметры многопроцессорной вычислительной системы. Максимальная производительность МВС составляет 18,8 терафлопс. В качестве вычислительных узлов используются 128 однотипных 16-ядерных Blade-серверов HP ProLiant BL685c, каждый из которых оснащен четырьмя четырехъядерными процессорами AMD Opteron 8356 2.3GHz и оперативной памятью в объеме 32 ГБ. В таблицах 2 и 3 приведены временные затраты выполнения одной итерации методом Якоби и МПТМ соответственно на различных сетках, а также значения ускорения и эффективности для различного числа вычислительных ядер.

Таблица 2

Ускорение и эффективность работы параллельного варианта метода Якоби

Из таблиц 2 и 3 видно, что максимальное значение эффективности достигалось на четырех вычислительных узлах и сетках 200х200. При этом возникает «суперлинейное ускорение». Эта аномалия вызвана следующей причиной. С увеличением количества вычислителей растёт суммарный объём их оперативной и кэш-памяти. Поэтому большая часть данных задачи вмещается в оперативной памяти и не требует подкачки с диска и вмещается в кэше.

Таблица 3

Ускорение и эффективность работы параллельного варианта МПТМ

Из приведенных таблиц также видно, что для каждой из расчетных сеток ускорение принимает наибольшее значение при определенном значении вычислителей, и при дальнейшем увеличении числа вычислительных ядер ускорение только уменьшается. Это связано с временными затратами на обмен данными между вычислителями. Из приведенных результатов расчетов видно, что методы с диагональными предобуславливателями (пример метод Якоби) лучше распараллеливаются, чем методы с треугольными предобуславливателями (пример МПТМ). Несмотря на это, параллельный вариант МПТМ является предпочтительнее метода Якоби для плохообусловленных задач, так как требует значительно меньшего числа итераций. Следует отметить, что адаптивный МПТМ нашел свое применение при решении задач аэродинамики [5; 10; 12] и транспорта донных материалов [7; 8].

Заключение

Работа посвящена параллельной реализации библиотеки итерационных решателей СЛАУ для задачи конвекции-диффузии на основе декомпозиции по одному пространственному направлению. Для решения двумерной задачи диффузии-конвекции была построена библиотека двухслойных итерационных методов, предназначенных для решения девятидиагональных сеточных уравнений. Получены табличные значения количества итераций решения сеточных уравнений итерационными методами от шага по временной переменной.

При параллельной реализации использованы методы декомпозиции сеточных областей по одному направлению для вычислительно трудоемких задач диффузии-конвекции, учитывающие архитектуру и параметры многопроцессорной вычислительной системы. Получены времена выполнения одной итерации методом Якоби и МПТМ соответственно на различных сетках, а также значения ускорения и эффективности параллельного алгоритма, зависящие от времени выполнения арифметической операции, времени передачи данных и латентности. Результаты использования многопроцессорных технологий показали, что максимальное значение эффективности достигалось на четырех вычислительных узлах и сетках 200х200 и равнялось 6,309 (метод Якоби) и 2,508 (метод МПТМ), а максимальное ускорение достигалось на 512 узлах и сетках 5000х5000 и равнялось 228,36 (метод Якоби) и 62,921 (метод МПТМ). Данные результаты расчетов говорят о том, что метод Якоби лучше распараллеливается по сравнению с методом МПТМ, однако, несмотря на это, для решения плохообусловленных задач параллельный МПТМ при больших шагах по временной переменной требует наименьшего числа итераций, что говорит о его предпочтении.

Работа выполнена при частичной финансовой поддержке Задания № 2014/174 в рамках базовой части государственного задания Минобрнауки России, а также при частичной финансовой поддержке РФФИ по проектам № 15-01-08619, № 15-07-08626 и № 15-07-08408.

Рецензенты:

Сухинов А.И., д.ф.-м.н., профессор, декан факультета физики, математики и информатики, ТГПИ им. А.П. Чехова (филиал) РИНХ, Таганрог;

Илюхин А.А., д.ф.-м.н., профессор, профессор кафедры математики, ТГПИ им. А.П. Чехова (филиал) РИНХ, Таганрог.