Вопрос перехода к компетентностно-ориентированной системе образования в России актуален уже, как минимум, последнее десятилетие. Образовательные стандарты нового поколения всё в большей степени нацелены на то, чтобы выпускники ВУЗов не просто обладали определенными знаниями по своей специальности, но и были максимально компетентными как в вопросах жизни общества, так и в профессиональных вопросах.
В соответствии с пунктом 5.2.41 постановления правительства Российской Федерации № 466 от 3 июня 2013 г., для большинства специальностей вводятся новые федеральные государственные образовательные стандарты. Новые стандарты, исходя из общих тенденций в российской системе образования, остаются компетентностно-ориентированными. Но их особенность заключается в том, что образовательные учреждения теперь имеют возможность самостоятельно определять содержание дисциплин, ориентируясь только на объем и список обязательных компетенций, установленных ФГОС.
Определение значимости компетенций
Всё это приводит к тому, что система образования становится более гибкой, а учебные заведения, факультеты, кафедры могут на своем уровне отслеживать последние тенденции в соответствующей профессиональной сфере и выстраивать процесс обучения, исходя из них. В связи с этими изменениями ФГОС возникает ряд новых научных задач, в частности, в области автоматизации процессов представления и оценки знаний. В статьях [1,2] описаны принципы, которые можно положить в основу решения этих задач. Кратко там говорится о возможности определения на основе комбинации экспертного анализа и массового опроса, степени важности отдельных компетенций в рамках какой-то конкретной специальности. В данной статье этот вопрос будет рассмотрен более подробно.
В роли экспертов должны выступить специалисты от различных организаций, руководство которых решит принять участие в работе данной системы, и методисты на кафедрах ВУЗов, также использующих данную систему. В массовом опросе примут участие студенты этих ВУЗов.
Соответственно, основными задачами в данном аспекте являются: разработка математической модели, которая позволит получать максимально обоснованное значение весовых коэффициентов компетенций и создание специального интернет-портала, с помощью которого будет проводиться экспертный анализ и массовый опрос. Такая система позволит наиболее точно определять весовые коэффициенты различных компетенций, развиваемых в процессе обучения по той или иной специальности. В указанных выше статьях [1, 2] говорилось, что эти весовые коэффициенты будут необходимы только при оценке профессиональной компетентности выпускника в целом. Теперь же, когда новые стандарты не столь категоричны в определении списка дисциплин и соответствующих им компетенций, эти данные могут быть также использованы каждым учебным заведением для составления конкретных учебных планов. При их подготовке методисты кафедр будут использовать списки компетенций, с соответствующими им весовыми коэффициентами, полученными, как уже говорилось, путем комбинирования экспертного анализа и массового опроса, в которых до этого этапа будут участвовать только работодатели, в качестве экспертов, и респонденты. Затем методисты подкорректируют коэффициенты, в соответствии с профилем учебного заведения и другими специфическими для него особенностями, выступив также в роли экспертов. Например, выпускник любого факультета МГУП им. Ивана Федорова должен быть в той или иной степени компетентен в области полиграфии или издательского дела, а для ВУЗа с другим профилем это будет не актуально. В таких вопросах экспертное мнение методистов и будет ключевым. На основе итоговых весовых коэффициентов для каждого конкретного образовательного учреждения будут формироваться учебные планы.
В данной статье не будут подробно рассматриваться вопросы, связанные с использованием полученных весовых коэффициентов. Они уже поднимались в статьях [1, 2]. В данной статье необходимо рассмотреть принципы, по которым будут пересекаться результаты экспертного анализа и массового опроса. Логично предположить, что основу итоговых выходных данных должна составлять компетентная экспертная оценка, а результат опроса сможет только в той или иной степени на нее повлиять. Планируется, что результаты экспертного анализа будут обрабатываться одним из традиционных методов, в несколько итераций, с использованием апостериорных оценок компетентности экспертов. Компетентность эксперта, в данном случае, будет оцениваться по степени согласованности его оценок с групповой оценкой объектов.
Влияние результатов массового опроса на экспертную оценку
Вывести формулы, в соответствии с которыми результат массового опроса будет влиять на экспертную оценку – одна из основных задач в рамках данной проблемы. При подсчете итоговых весовых коэффициентов будет учитываться количество проголосовавших респондентов и среднеквадратическое отклонение множества данных ими оценок.
Пусть M – множество оценок массового опроса, m – среднее арифметическое значение этого множества, Ϭ – среднеквадратическое отклонение результата массового опроса, vϬ – коэффициент вариации результата массового опроса, n – количество респондентов, Ɛ – результат экспертной оценки. Как эксперты, так и респонденты, будут оценивать компетенции по шкале от 0 до 100 баллов. Итоговая оценка компетенции (I) также будет находиться в этом диапазоне. Однако весовой коэффициент компетенции, с которым как раз и будет осуществляться дальнейшая работа, будет представлять собой десятичную дробь, округленную до сотых единиц. Поэтому по формуле 1 вычисляется итоговая оценка, а в формуле 2 эта оценка делится на 100 и получается уже весовой коэффициент.
(1)
(2)
Здесь k – некоторый коэффициент, принадлежащий промежутку от 0 до 1 и характеризующий объективность результатов массового опроса. Эта формула при k равном нулю не влияет на значение экспертной оценки, а при k равном единице возвращает среднее арифметическое значение результатов экспертной оценки и массового опроса, то есть в этом случае влияние результатов массового опроса максимально. Значение данного коэффициента должно зависеть от двух параметров: коэффициента вариации значений массового опроса и количества респондентов. Причем, это значение должно быть максимальным только при достаточно низком разбросе результатов массового опроса и относительно высоком количестве опрошенных людей.
Таким образом, формула вычисления данного коэффициента должна содержать в себе два множителя. Соответственно, первый множитель должен зависеть от коэффициента вариации, второй – от количества респондентов. Рассмотрим в отдельности, каким образом необходимо сформировать каждый из этих множителей.
В данной статье не будут подробно описываться традиционные для таких наук, как статистика и теория вероятностей, понятия. Однако дать краткую характеристику некоторым показателям и величинам, используемым в данной работе, необходимо. Как уже было сказано, в основе первого множителя будет лежать так называемый коэффициент вариации, который рассчитывается по формуле 3:
(3)
В формуле 3, 
– это среднее значение оценок, которые выставляют респонденты некоторой компетенции, а 
– среднеквадратическое отклонение результатов массового опроса. В теории вероятностей и статистике среднеквадратическим отклонением называют один из наиболее распространенных показателей разброса значений случайной величины относительно ее среднего значения. В данном случае, в качестве случайной величины выступают оценки, выставляемые респондентами различным компетенциям для той или иной специальности. Оценки будут выставляться в диапазоне от 0 до 100. И если среднеквадратическое отклонение – это абсолютная величина, измеряемая в тех же единицах, что и само значение, то коэффициент вариации, получаемый в формуле 3 – величина относительная, измеряемая в процентах.
В статистике есть закрепившиеся представления о значении коэффициента вариации. Так вариация в пределах 10 % считается незначительной, а данные в таком случае однородными, 10–20 % – средняя вариация, от 20 до 33 % – значительная. Если же вариация превышает 33 %, то данные считаются неоднородными. В таком случае из выборки исключают нетипичные наблюдения. Это необходимо учитывать при формировании первого множителя.
Значение первого множителя должно находиться в интервале [0, 1]. При этом единице он должен быть равен при максимальной однородности данных. При превышении коэффициентом вариации значения в 33 % множитель должен максимально приближаться к нулю. Если представлять значение множителя функцией в общем виде, то эта функция должна выглядеть как 
, где k – константа. Однако подобрать такую константу, при которой бы значение функции было равно единице при коэффициенте вариации в пределах 10 %, а затем плавно уменьшалось, и уходило в ноль при коэффициенте вариации равном 33 %, нельзя (рисунок 3).
Поэтому целесообразно представить данный множитель в виде кусочно-заданной функции f(vϬ), которая при vϬ, не превышающем 10 %, возвращает единицу, а при vϬ>10 плавно уходит в ноль, достигнув среднего значения множителя при vϬ близком к 20 %.
Такую функцию в общем виде можно представить так:
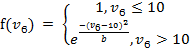(4)
где b – некоторая константа.
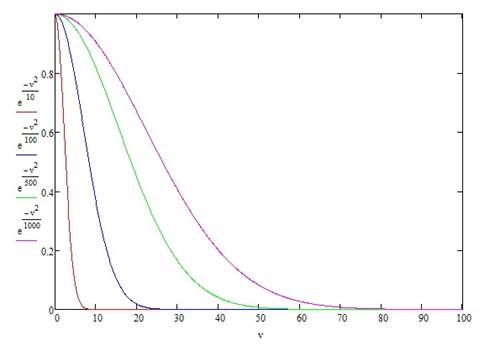
Рис.1
Константу b определим также, исходя из фактического понимания значений коэффициента вариации. Как было написано выше, 
– это некоторое пороговое значение, после которого данные принято считать неоднородными. Таким образом, при первый множитель должен еще, при достаточно большом количестве респондентов, влиять на итоговую оценку компетенции, но при этом уже быть максимально близким к нулю.
Теперь необходимо разобраться, при каком минимальном значении данного множителя, коэффициент еще может повлиять на общую оценку компетенции. Для этого допустим, что количество респондентов достаточно велико и второй множитель равен единице. Также учтем, что весовой коэффициент в итоге округляется до сотых единиц. Рассмотрим предельный случай, когда мнение экспертов и респондентов различается на 100 %. То есть, например, эксперты оценили некоторую компетенцию в 100 баллов, а в результате опроса эта компетенция получила 0 баллов (при этом, как уже было написано, количество респондентов было достаточно велико, чтобы учитывать это мнение). Необходимо определить такой коэффициент объективности массового опроса, при котором бы в таких условиях итоговая оценка отличалась от экспертной на один процент. Это значение и должно соответствовать пороговому коэффициенту вариации массового опроса, равному 33 %. С помощью пакета Mathcad вычисляем значение коэффициента объективности массового опроса при экспертной оценке компетенции равной 100 и результате опроса равном нулю. Это значение равно 0,02.
Теперь вернемся к формуле 4, содержащей константу b, значение которой необходимо определить. Выше было посчитано значение коэффициента объективности массового опроса, которое должно соответствовать коэффициенту вариации равному 33 %. Ранее мы приняли множитель, который характеризует количество респондентов в формуле определения коэффициента объективности равным единице. Это значит, что первый множитель, который мы находим по формуле 4, в таких условиях будет равен посчитанному коэффициенту объективности. Поэтому теперь из формулы 4 с помощью Mathcad находим значение константы b при коэффициенте вариации 33 % и значении зависящего от него множителя, равном 0,02. Это значение равно 135,224.
Подставим это значение в формулу 4. И построим в Mathcad график зависимости первого множителя от коэффициента вариации.
Рис. 2
На графике (рисунок 2) видно, что значение, возвращаемое функцией, при коэффициенте вариации менее 10 % равно единице, при 10–20 % плавно уменьшается от 1 до 0,5, а при коэффициенте 20–33 % опускается до минимального значения и далее уходит в ноль. Таким образом, график соответствует условиям, описанным выше. То есть первый множитель (назовем его 
), используемый для подсчета коэффициента объективности массового опроса и зависящий от коэффициента вариации, будет определяться следующим образом:
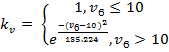(5)
Второй множитель в рамках данной статьи подробно рассматриваться не будет, так как этот вопрос требует отдельного изучения и обсуждения. Однако несколько слов написать о нем необходимо. Как было указано выше, он также должен находиться в диапазоне от 0 до 1. Достигать значений, близких к максимальным, множитель должен только тогда, когда количество респондентов приблизится к значениям определенного порядка. И порядок этой величины как раз является одним из основных вопросов, в данном случае. Применение массового опроса для определения степени важности отдельных компетенций, наряду с экспертных анализом, необходимо для учета мнения, в первую очередь, студентов, являющихся непосредственными участниками учебного процесса. Если допустить, что после разработки и запуска данная система будет использоваться во всех ВУЗах страны, то при определении необходимого количества проголосовавших людей можно отталкиваться от статистических данных об общем количестве студентов в России. Это примерно 6 миллионов человек. Естественно, эта цифра меняется каждый год, но не так значительно. И в таком случае порядок достаточного количества респондентов можно взять равный одному миллиону. Однако на практике такой крайне упрощенный подход не приемлем. Хотя отталкиваться в данном вопросе всё равно необходимо от статистических данных. Но не от общих данных по стране, а от данных по конкретным ВУЗам, принявшим участие в работе системы. То есть планируется, что в систему будут поступать данные о студентах ВУЗов, использующих систему. Исходя из этих данных, можно будет делать определенные выводы о степени массовости проводимых исследований. Кроме того, предполагается, что студенты будут регистрироваться не самостоятельно, а централизованно, учебными заведениями, принимающими участие в работе системы. Это позволит избежать создания фальшивых страниц студентов. Естественно, весь этот процесс будет максимально автоматизирован. Как говорилось в статьях [1, 2], планируется сделать несколько категорий пользователей на портале, у каждой из которых будут свои возможности.
Заключение
Основная цель данных разработок – увеличение степени взаимодействия работодателей и студентов с научно-педагогическим составом образовательных учреждений и, соответственно, уровня влияния рынка труда и общества на процесс формирования учебных программ.
Рецензенты:
Майков К.А., д.т.н., профессор кафедры программного обеспечения ЭВМ и информационных технологий МГТУ имени Н. Э. Баумана, г. Москва;
Николаев А.Б., д.т.н., профессор, декан факультета «Управление», заведующий кафедрой «Автоматизированные системы управления» ФГБОУ ВПО «Московский автомобильно-дорожный государственный технический университет (МАДИ)», г. Москва.