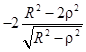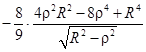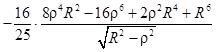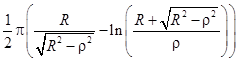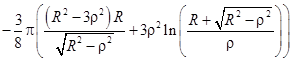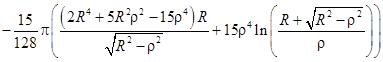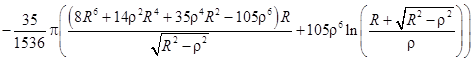При внесении проводящей пластины во внешнее электростатическое поле на поверхности пластины индуцируются электрические заряды. Соотношение, связывающее потенциал внешнего поля 
и потенциал на поверхности проводящей пластины 
с распределением индуцированного заряда, можно записать в виде [3, 4]:
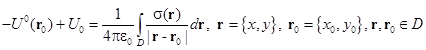(1)
Таким образом, при известном распределении зарядов 
на поверхности проводящей пластины можно определить алгебраическую сумму распределения потенциала внешнего поля и потенциала на поверхности пластины . В натурных экспериментах обычно известно распределение потенциала внешнего поля, потенциал поверхности проводника всегда можно измерить или удерживать его под постоянным напряжением. Поэтому представляет интерес обратная задача – задача определения распределения зарядов на поверхности проводника. В соответствии с выражением (1) нужно решить интегральное уравнение Фредгольма первого рода относительной искомой величины. Величина есть суммарное распределения зарядов на проводнике с разных сторон пластины, и поэтому следующий шаг заключается в разделении зарядов соответствующих стороне, обращенной к источнику поля и противоположной стороны. Для разделения зарядов необходимо использовать нормальную составляющую напряженности результирующего поля
. (2)
Напряженность поля связанна с зарядами соотношениями:
, (3)
из которых можно получить:
. (3)
Цель работа заключается в том, чтобы заменить сложное интегральное уравнение (1) алгебраическим с помощью полученных автором полиномов, то есть получить аналитические соотношения, связывающие потенциал результирующего поля и распределение зарядов на проводнике.
Постановка задачи. Будем предполагать, что внешнее поле обладает симметрией вращения относительно оси симметрии диска. Тогда уравнение (1) может быть переписано в виде
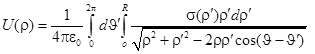, (4)
здесь 
– результирующий потенциал.
Последнее выражение можно переписать с использованием эллиптического интеграла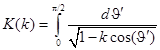 
тогда соотношение (4) преобразуется в следующее выражение
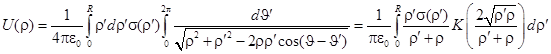. (5)
Учитывая преобразование Ландена [2,3,4] можно получить следующее свойство эллиптического интеграла:
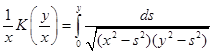. (6)
Полученное свойство позволяет записать неизвестную подынтегральную функцию 
через известный потенциал 
:
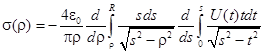(7)
Определим распределение зарядов, порожденное потенциалом вида
(8)
После подстановки (8) в (7) получаем выражения для распределения зарядов в виде полиномов 
при четных и нечетных 
соответственно:
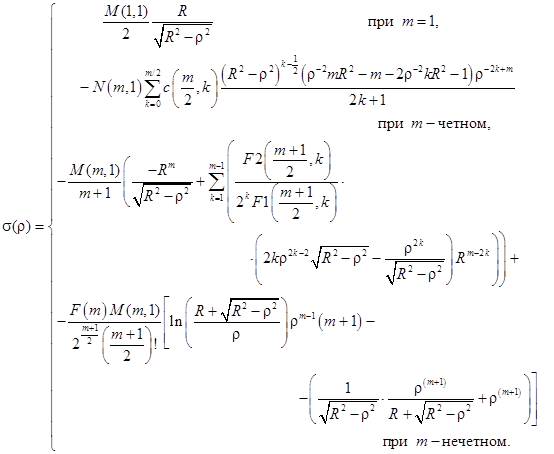
Здесь
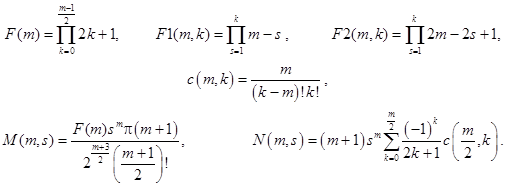
Приведем несколько четных степеней
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
и нечетных степеней
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Используя табличные соотношения, можно определить интересующее нас распределение зарядов при известном распределении потенциала. Для этого необходимо представить распределение потенциалов поля в виде разложения по многочленам
(9)
Коэффициенты разложения ряда (9) легко определить, используя методом наименьших квадратов. Распределение зарядов при этом определяется соотношением:
(10)
Вид полиномов ряда (8) определяется выражением из таблицы.
В случае диска с отверстием в выражении (5) изменятся пределы интегрирования:
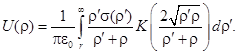(11)
В этом случае нет необходимости рассчитывать новые полиномы для разложения распределения зарядов. Достаточно осуществить необходимое преобразование системы координат, заключающееся в проецировании внешней области круга на внутреннюю область. Путем замены переменных перейдем от интегрального выражения (11) к интегральному выражению (5),с помощью сопряженных координат:
, 
. (12)
В результате получим интегральное выражение с новыми пределами интегрирования
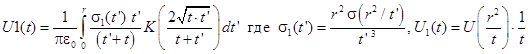(13)
В качестве работы полиномиального алгоритма рассмотрим примеры, имеющие аналитическое решение[1, 2].
Пример 1: Определим распределение зарядов на заземленном диске радиуса 
, если диск помещен во внешнее поле точечного заряда, расположенного на оси диска на расстоянии 
от поверхности диска. Отношение 
в задаче выберем 1.
Потенциал точеного заряда в плоскости диска и суммарное распределение зарядов на диске определяются выражениями соответственно[1]:
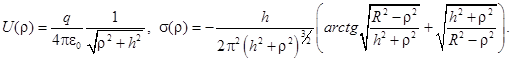(15)
Представим потенциал в виде ряда:
(16)
Определим коэффициенты разложения (12), используя метод наименьших квадратов. Для этого зададимся числом коэффициентов разложения
.
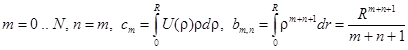
Определяем коэффициенты разложения am, решая матричное уравнение:
– единичная матрица, 
, 
– параметр регуляризации, уменьшающий относительный вклад шумовой составляющей в решении[1, 5].
В результате численного расчета коэффициентов cm получаем коэффициенты разложения
|
m |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
am |
0,265 |
0 |
-1.43 |
-1.438 |
29.7 |
-104.7 |
198.4 |
-229.6 |
162.7 |
-65.06 |
11.273 |
А искомое поверхностное распределение зарядов будет определяться выражением с рассчитанными коэффициентами:
Результаты расчетов приведены на рисунке:
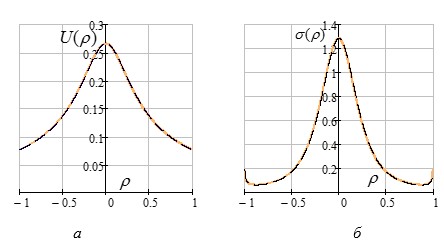
Рис 1. а) потенциал внешнего поля как аналитическая функция и результат ее разложения в ряд (12),
б) распределение зарядов как аналитическая зависимость и результат восстановления в виде ряда (13)
На рисунках демонстрируется хорошее совпадение аналитических зависимостей и зависимостей, полученных полиномиальным методом.
Пример 2: Определим распределение зарядов на поверхности проводящего диска с круговым отверстием 
, если диск помещен во внешнее поле точечного заряда, расположенного на оси диска на расстоянии 
от поверхности диска с радиусом 
.
Потенциал точеного заряда в плоскости диска и суммарное распределение зарядов на диске определяются выражениями соответственно[3,4]:
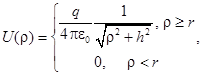
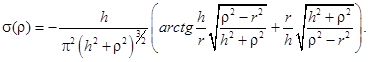(17)
В данном случае будет использоваться уравнение (5) с заменой переменных:
, . (18)
В результате получаем интегральное выражение с новыми пределами интегрирования
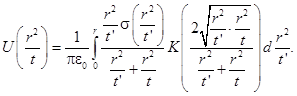(19)
Упрощая выражение (19), получаем
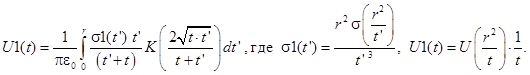(20)
Представим потенциал поля 
в виде ряда
(21)
По тому же алгоритму определяем коэффициенты разложения am, затем, используя таблицу полиномов и используя замену переменной в виде 
, находим
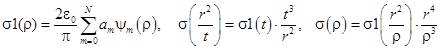. (22)
Полученное распределение зарядов 
на поверхности проводника приведено на рисунке 2, там же приведен результат, полученный по аналитической формуле [3,4].
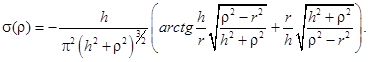
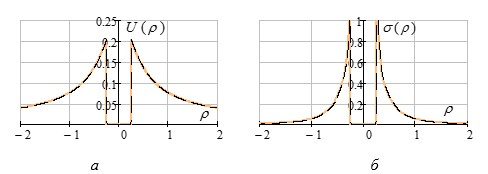
Рис. 2.а) потенциал внешнего поля как аналитическая функция и результат ее разложения в ряд (21),
б) распределение зарядов как аналитическая зависимость и результат восстановления в виде ряда (22)при
– параметр регуляризации
Выводы
Автору удалось получить полиномы, позволяющие свести интегральное уравнение, связывающее распределения зарядов на пластине с внешним статическим полем, к более простому алгебраическому уравнению. Полиномиальный алгоритм справедлив при аксиально симметричном внешнем поле и аксиально симметричной форме пластины. При использовании полиномиального метода необходимо производить регуляризацию коэффициентов разложения для уменьшения влияния шумов алгоритма.
Рецензенты:
Усов Ю.П., д.т.н., профессор кафедры ЭСиЭ ЭНИН ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет», г. Томск;
Сивков А.А., д.т.н., профессор кафедры ЭПП ЭНИН ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет», г. Томск.