В настоящее время существуют эффективные методики выбора трасс трелевочных волоков лесосек [3], рассмотрены вопросы их компьютерного проектирования [4], проведены исследования, посвященные моделированию размещения погрузочных пунктов и сети волоков на лесосеке с использованием лингвистических переменных в качестве структур для моделирования [5] и покрытия гиперсети взвешенным корневым деревом [1, 2] из условия минимизации повреждения грунта. Исследования [7, 8] предусматривают эффективный анализ выбора функционального назначения транспортных путей.
В то же время в отмеченных научных работах уделено недостаточное внимание одновременному, комплексному учету всего разнообразия возможных вариантов размещения магистральных волоков и погрузочных пунктов на лесной территории по критерию минимизации затрат на освоение лесного квартала, что особенно актуально в условиях поквартального освоения участков лесного фонда [6, 9, 10].
Цель исследования: сокращение затрат на обустройство погрузочных пунктов, прокладку магистральных волоков и трелевку лесоматериалов в границах лесного квартала в условиях существующей сети лесовозных дорог.
Материал и методы исследования. При анализе вариантов поквартального освоения участков лесного фонда существует возможность наглядного изображения лесного квартала и находящихся на его территории делянок в виде схемы, представляющей собой связи между определенными парами вершин, характеризующими основные элементы анализируемой ситуации, соединенными посредством ребер. В качестве таких вершин могут быть приняты различные варианты размещения погрузочных пунктов и участков лесосек, а в качестве ребер использованы возможные варианты соединяющей их сети транспортных путей (поквартальных просек, лесовозных дорог, технологических коридоров, магистральных и пасечных волоков). Подобное представление лесного квартала является эффективным инструментом для формулировки и решения задач его обустройства и размещения на его территории основных технологических элементов для выполнения всего комплекса лесосечных работ.
Пример постановки задачи структуризации погрузочных пунктов и магистральных волоков в пределах лесного квартала приведен на рисунке 1, где показана схема с вариантами размещения погрузочных пунктов и транспортных путей. Число анализируемых элементов может быть различно и проектируется в зависимости от условий местности: рельефа, почвенно-грунтовых условий, территориального размещения выделов, требующих на разных этапах своего развития различных мероприятий, класса возраста и состояния древостоя, наличия заболоченных участков, прогалин и т. д. Для получения результатов, более точно отражающих реальную ситуацию, при построении технологической карты лесного квартала с указанием расположенных на его территории участков может быть допущена дополнительная детализация их геометрических характеристик, связанная с разделением всех или части крупных лесосек вытянутой формы на ряд небольших участков, характеризующихся своими «центрами тяжести» выполняемых работ. На представленном рисунке подобная детализация и предпринята для разделения на участки двух выделов, в результате которой получены участки лесосек с центрами тяжести, обозначенными номерами 4, 5 и 7, 8, 9.
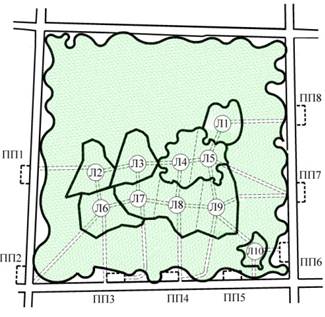
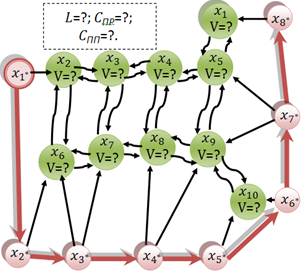
Рис. 1. Постановка задачи выбора схемы размещения транспортных путей в лесном квартале
Для построения графа введем обозначения наиболее вероятных мест размещения погрузочных пунктов (ПП1, ПП2, …, ППi*, …ППk) и, обозначив центры тяжести каждого участка лесосеки (Л1, Л2, …, Лi, …Лn), соединим их ребрами на графе в соответствии с наиболее вероятными направлениями трелевки древесины.
Очевидно, что при увеличении числа возможных вариантов размещения погрузочных пунктов и числа разрабатываемых лесосек (делянок) на территории лесного квартала, а также в зависимости от уровня детализации принятых при построении схемы транспортных путей на его территории число вариантов остовов графов растет в геометрической прогрессии.
Постановка задачи предполагает:
-
анализ затрат на обустройство погрузочных пунктов
;
-
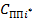определение возможных расстояний трелевки с учетом длин анализируемых транспортных путей предварительной транспортной сети;
-
обоснование возможных затрат на прокладку 1 п. м каждого трелевочного волока
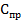в зависимости от природных условий лесных участков, через которые они будут проложены;
-
определение стоимости машиносмены
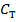при трелевке древесины.
Линиям, ведущим от места предполагаемого расположения погрузочного пункта к участку лесосеки, присваивается значение , равное значению стоимости подготовки погрузочного пункта, необходимого для использования данного направления. Линиям, соединяющим погрузочные пункты между собой, а также соединяющим между собой участки лесосек, присваивается значение 
, свидетельствующее о том, что использование данных транспортных путей не вызывает необходимости обустройства погрузочного пункта. Использование данного показателя позволит сократить число погрузочных пунктов, поскольку становится очевидным, что внедрение в граф нового магистрального волока предусматривает дополнительные материальные затраты на обустройство примыкающего погрузочного пункта. Все вершины, характеризующие погрузочные пункты, должны быть связаны между собой ребрами, соответствующими поквартальным просекам, но не образовывать замкнутого цикла.
Анализируя существующие алгоритмы поиска кратчайшего каркаса графа, можно отметить, что наиболее известные в настоящее время алгоритмы Краскала, Прима, Соллина, Тарьяна—Черитона не могут быть применены в данной ситуации ввиду того, что в этом случае мы имеем дело с ориентированным графом, предусматривающим трелевку лишь в направлении к погрузочным пунктам. В то же время алгоритм Эдмондса, дающий возможность поиска минимального по весу оркаркаса и предусматривающий просмотр вершин графа в произвольном порядке, также не может быть использован в данной ситуации, поскольку весовые характеристики дуг, входящих в орграф, изменяются в зависимости от перечня дуг, вошедших в оркаркас и соединяющих анализируемую вершину с его корнем.
Предлагаемый алгоритм решения задачи выбора схемы размещения транспортных путей в лесном квартале относится к жадным алгоритмам и позволяет осуществить выбор кратчайшего оркаркаса при решении частной задачи выбора схемы размещения транспортных путей в лесном квартале посредством разрастания одного поддерева графа (обозначим его 
), содержащего больше одной вершины.
На практике ведения лесосечных работ в квартале отчетливо видно, что расстояние трелевки и затраты на трелевку с каждого нового анализируемого участка должны учитывать удаленность от погрузочного пункта предыдущего участка, через территорию которого проложен волок. Таким образом, особенностью задачи размещения транспортных путей в лесном квартале является то, что вес каждой присоединяемой к поддереву дуги не может быть известен на начальной стадии проектирования, а зависит от состава дуг, включенных в поддерево на предыдущих этапах анализа. Алгоритм предусматривает последовательное частичное увеличение веса каждой следующей присоединяемой к поддереву графа дуги за счет веса всех или части дуг, присоединенных к нему ранее.
Для реализации предлагаемого алгоритма вершины графа пронумерованы так, чтобы вершина 
, соответствующая корню оркаркаса, получила номер 
. Принимаем 
.
Затраты на прокладку магистрального волока, обустройство погрузочного пункта и трелевку лесоматериалов с анализируемого участка лесного фонда 
на погрузочный пункт 
можно найти по формуле:
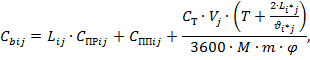
где 
— расстояние между смежными участками лесного фонда и 
, между которыми анализируется возможность прокладки магистрального волока, м; 
— стоимость прокладки магистрального волока, связывающего между собой анализируемую вершину (участок лесосеки) с предыдущей вершиной (участком лесосеки), руб.; 
— стоимость обустройства погрузочного пункта для трелевки лесоматериалов с участка , руб. (указывается в тех случаях, когда анализируемый магистральный волок (ребро) примыкает непосредственно к погрузочному пункту (вершине ); — стоимость машиносмены при трелевке, руб./смена;
— вырубаемый запас на анализируемом участке лесной площади, м3; 
—трудозатраты при сборе и разгрузке пачки лесоматериалов, с; 
— расстояние между погрузочным пунктом и анализируемым участком лесного фонда , м; 
— средняя скорость движения машины, задействованной на трелевке, при движении в холостом и грузовом направлениях на участке между погрузочным пунктом и анализируемым участком лесного фонда , м/с;
– средний объем трелюемой пачки лесоматериалов, м3; 
– время смены, ч; 
– коэффициент использования времени смены.
Каждой вершине, последовательно включаемой в поддерево 
, присваивается пометка [
; 
]. В данной пометке 
есть вершина поддерева 
ближайшая к вершине , присоединяемой к поддереву, а — вес присоединяемой дуги графа, лежащей между вершинами 
.
При наличии существующих лесовозных дорог вершины, обозначающие погрузочные пункты, соединяются между собой ребрами уже на первом этапе функционирования алгоритма. Получим:
В ходе дальнейшего анализа поддерево графа постепенно разрастается за счет присоединения ребер 
, где 
.
При каждой новой итерации одна из вершин графа 
присоединяется к поддереву посредством добавления дуги , либо, во избежание образования циклов, происходит обновление поддерева путем замены одной из входящих в него дуг на дугу с более низким весом. Добавленная дуга должна иметь минимальный вес из всех примыкающих к поддереву дуг. При добавлении к поддереву 
новой вершины возникает необходимость пересмотра пометок [; ] у всех вершин, примыкающих к последней присоединенной к поддереву вершине. При этом анализируются как примыкающие вершины, принадлежащие поддереву 
, так и вершины, не принадлежащие ему 
.
Если в результате анализа получен цикл с существующими дугами поддерева, т.е. выявлена вершина 
, вес которой может быть уменьшен в результате последующей итерации, то из поддерева следует удалить дугу, которая входила в узел на предыдущей итерации. Происходит разрыв орцепи, и все вершины, соединенные ранее с вершиной посредством исходящих из нее дуг, исключаются из поддерева и теряют свои пометки.
Анализ продолжается до тех пор, пока каждая из вершин графа не получит пометку, вес которой будет соответствовать минимальному значению веса из всех соответствующих показателей входящих в нее дуг, а число ребер в поддереве не станет равным 
(где 
– общее число лесных участков, 
– общее число погрузочных пунктов).
Полученное дерево можно будет принять в качестве кратчайшего оркаркаса графа, а, следовательно, и в качестве рационального варианта размещения сети трелевочных путей в анализируемом квартале.
Результаты исследования и их обсуждение. Результаты выполненных расчетов с использованием предложенного алгоритмического подхода обоснования методики размещения транспортных путей в лесном квартале доказали возможность снижения материальных затрат на обустройство погрузочных пунктов, прокладку транспортных путей и трелевку лесоматериалов на величину до 18%. При этом расчетный экономический эффект использования алгоритма составил 26 руб./м3.
Выводы. Предложенная методика позволяет получить рациональный вариант размещения магистральных волоков при поквартальном освоении участков лесного фонда, сократить затраты на обустройство погрузочных пунктов, прокладку транспортных путей и трелевку по ним лесоматериалов.
Рецензенты:
Войтко П.Ф., д.т.н., профессор, ФГБОУ ВПО «Поволжский государственный технологический университет», г. Йошкар-Ола;
Царев Е.М., д.т.н., доцент ФГБОУ ВПО «Поволжский государственный технологический университет», г. Йошкар-Ола.