Наиболее надежно использовать экспериментальные методы определения теплоемкости (например, калориметрические измерения). Однако задача осложняется тем, что большинство веществ, теплоемкость которых не известна, трудно получить в чистом виде. Кроме того, таких соединений может быть слишком много, что делает весьма трудоемкой задачу их экспериментального получения, очистки и определения свойств.
Задачей данной работы является на примере низкокипящих метилхлорсиланов определить применимость некоторых известных эмпирических расчетных методов для определения теплоемкости жидкости и пара и определить коэффициенты соответствующих уравнений для расчета свойств высококипящих метилхлорсиланов. В качестве источника данных по теплоемкости низкокипящих метилхлорсиланов использовалась база данных программы ChemCAD [5].
Расчет теплоемкости газа. Достаточно высокую точность расчета теплоемкости газа показали аддитивно-групповые методы [4]. Для соединений, групповые вклады для которых определены на основе экспериментальных значений теплоемкости при различных температурах, погрешность расчета теплоемкости такими методами в большинстве случаев оказывается ниже 5%. Групповые вклады известных методов расчета теплоемкости газа табулированы для различных органических соединений. Возможен учет в структуре соединений таких атомов, как O, Cl, N, S. Данные по атому Si для расчета свойств кремнийорганических соединений отсутствуют.
Для кремнийорганических соединений известен упрощенный вариант аддитивно-группового метода [2]. Согласно этому методу теплоемкость газа метилхлорсиланов при заданной температуре определяется как аддитивная сумма вкладов заместителей при одном атоме кремния. Табулированы вклады заместителей в интервале температур от 300 К до 1000 К. В качестве заместителей рассмотрены такие группы, как Н, Me, Et, Ph и Cl. Проверка точности этого метода для основных метилхлорсиланов и хлорсиланов показала, что погрешность расчета составляет не более 5%. На основании данных работы [2] можно рассчитать теплоемкость различных производных моносилана. Однако при наличии в молекуле двух и более атомов кремния данный метод оказывается неприменимым, так как отсутствуют опубликованные значения вкладов для таких структурных элементов, как Si–Si, Si–O–Si и Si–CH2–Si.
С целью расширения возможностей метода, изложенного в работе [2], нами был выполнен пересчет групповых вкладов на вклады составляющих связей. При этом теплоемкость газа при заданной температуре будет определяться как аддитивная сумма вкладов составляющих связей для данной температуры. Для пересчета использовались данные работ [2] и [3] и известные температурные зависимости теплоемкости газа для кремнийорганических соединений [5]. Рассчитанные значения вкладов составляющих связей приведены в таблице 1.
Таблица 1
Значения вкладов составляющих связей для расчета теплоемкости идеального газа метилхлорсиланов
|
тип связи |
вклад кал/моль.К при |
|||||
|
300 К |
400 К |
500 К |
600 К |
800 К |
1000 К |
|
|
С–С |
2,06 |
2,585 |
2,975 |
3,235 |
3,585 |
3,730 |
|
С–Н |
1,72 |
2,1825 |
2,6373 |
3,0575 |
3,7425 |
4,305 |
|
Si–H |
1,9605 |
2,6377 |
3,283 |
3,8325 |
4,5862 |
5,0117 |
|
Si–Cl |
5,43 |
5,8383 |
6,0565 |
6,1775 |
6,3258 |
6,4463 |
|
Si–C |
3,587 |
3,7785 |
3,9083 |
3,997 |
4,1363 |
4,0815 |
|
Si–O |
3,004 |
3,2861 |
3,5531 |
3,7558 |
3,8434 |
3,9801 |
|
Si–Si |
3,706 |
3,5232 |
3,467 |
3,46 |
3,3112 |
2,8562 |
Погрешность расчета теплоемкости газа для метилхлорсиланов при использовании полученных вкладов составляющих связей не превышает 5% при температуре 300 К. При температурах более 400 К погрешность расчета теплоемкости газа менее 3%. Исключением является диметилхлорсилан (при 300 К погрешность расчета составляет 7,4%; при 400 К погрешность расчета составляет 4,9%).
Данные по теплоемкости газа метилтрихлорсилана (MeSiCl3), приведенные в базе данных программы ChemCAD [5], кардинально отличаются от всех данных, как опубликованных в литературе, так и рассчитанных по аддитивной схеме. Поскольку источник данных в [5] не указан, использовать теплоемкость метилтрихлорсилана из базы [5] представляется нерациональным без дополнительной проверки. Для расчета температурной зависимости теплоемкости газа метилтрихлорсилана целесообразно применять данные работы [3].
С помощью приведенных в таблице 1 значений вкладов составляющих связей нами была впервые рассчитана температурная зависимость теплоемкости газа Cp(T) некоторых высококипящих кремнийорганических соединений, образующихся в ходе прямого синтеза метилхлорсиланов. Полученные данные аппроксимировались следующими уравнениями:
![]() , кал/моль.К (1)
, кал/моль.К (1)
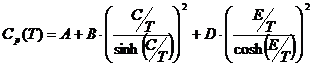 , Дж/кмоль.К (2)
, Дж/кмоль.К (2)
где Т – температура, К;
A, B, C и D – коэффициенты уравнения
Для инженерных расчетов уравнения (1) и (2) являются равнозначными с точки зрения точности получаемого результата. Выбор одного из этих уравнений для расчета теплоемкости газа определяется возможностями используемых программных средств.
Коэффициенты уравнений (1) и (2) приведены в таблицах 2 и 3. Интервал применимости от 300 К до 1000 К.
Таблица 2
Коэффициенты уравнения (1) для расчета теплоемкости идеального газа высококипящих продуктов прямого синтеза метилхлорсиланов (кал/моль.К)
|
вещество |
A |
B |
С |
D |
|
Me3Si–SiClMe2 |
23,83785 |
0,10655 |
-3,18082e-005 |
-4,31235e-009 |
|
Cl3Si–O–SiCl3 |
21,05719 |
0,08549 |
-1,02807e-004 |
4,29051e-008 |
|
Me2ClSi–O–SiClMe2 |
21,00980 |
0,12264 |
-7,17417e-005 |
1,69133e-008 |
|
MeCl2Si–O–SiCl2Me |
21,03350 |
0,10406 |
-8,72744e-005 |
2,99092e-008 |
|
Me3Si–SiCl2Me |
23,84970 |
0,09727 |
-3,95746e-005 |
2,18559e-009 |
|
Me2ClSi–SiCl2Me |
23,86155 |
0,08798 |
-4,73410e-005 |
8,68353e-009 |
|
(SiCl3)2 |
23,89709 |
0,06011 |
-7,06400e-005 |
2,81774e-008 |
|
Me2ClSi–SiClMe2 |
23,84970 |
0,09727 |
-3,95746e-005 |
2,18559e-009 |
|
Me2ClSi–O–SiCl2Me |
21,02165 |
0,11335 |
-7,95081e-005 |
2,34113e-008 |
|
MeCl2Si–SiCl2Me |
23,87339 |
0,07869 |
-5,51073e-005 |
1,51815e-008 |
|
Me3Si–CH2–SiClMe2 |
24,72109 |
0,13160 |
-5,01095e-005 |
1,98157e-009 |
|
Me3Si–CH2–SiCl2Me |
24,73294 |
0,12231 |
-5,78759e-005 |
8,47951e-009 |
|
Me2ClSi–CH2–SiClMe2 |
24,73294 |
0,12231 |
-5,78759e-005 |
8,47951e-009 |
|
Me2ClSi–CH2–SiCl2Me |
24,74479 |
0,11302 |
-6,56422e-005 |
1,49775e-008 |
|
MeCl2Si–CH2–SiCl2Me |
24,75663 |
0,10373 |
-7,34086e-005 |
2,14754e-008 |
|
(SiCl3)2SiCl2 |
35,26003 |
0,07492 |
-8,56537e-005 |
3,27786e-008 |
Таблица 3
Коэффициенты уравнения (2) для расчета теплоемкости идеального газа высококипящих продуктов прямого синтеза метилхлорсиланов (Дж/кмоль.К)
|
вещество |
A |
B |
С |
D |
E |
|
Me3Si–SiClMe2 |
160729,37 |
322114,11 |
1226,34 |
158492,04 |
527,81 |
|
Cl3Si–O–SiCl3 |
146106,25 |
52339,68 |
1544,11 |
74037,27 |
685,85 |
|
Me2ClSi–O–SiClMe2 |
158812,53 |
285567,24 |
1223,75 |
156225,70 |
533,62 |
|
MeCl2Si–O–SiCl2Me |
167568,34 |
172897,66 |
1694,42 |
131917,40 |
749,94 |
|
Me3Si–SiCl2Me |
148726,47 |
288311,09 |
1407,02 |
187048,78 |
600,90 |
|
Me2ClSi–SiCl2Me |
159273,14 |
200867,65 |
1297,90 |
112260,18 |
599,28 |
|
(SiCl3)2 |
141538,57 |
30021,38 |
1455,42 |
52214,24 |
697,37 |
|
Me2ClSi–SiClMe2 |
148726,47 |
288311,09 |
1407,02 |
187048,78 |
600,90 |
|
Me2ClSi–O–SiCl2Me |
177221,64 |
212627,01 |
1589,22 |
152329,87 |
744,22 |
|
MeCl2Si–SiCl2Me |
153009,47 |
146507,99 |
1326,81 |
94088,08 |
617,96 |
|
Me3Si–CH2–SiClMe2 |
181704,34 |
375840,23 |
1207,44 |
174576,48 |
506,53 |
|
Me3Si–CH2–SiCl2Me |
170221,50 |
329170,90 |
1283,66 |
187173,22 |
553,89 |
|
Me2ClSi–CH2–SiClMe2 |
170221,50 |
329170,90 |
1283,66 |
187173,22 |
553,89 |
|
Me2ClSi–CH2–SiCl2Me |
194674,00 |
256654,01 |
1642,18 |
171334,59 |
756,38 |
|
MeCl2Si–CH2–SiCl2Me |
174692,13 |
198369,78 |
1374,28 |
127491,78 |
634,05 |
|
(SiCl3)2SiCl2 |
199698,29 |
38151,03 |
1450,54 |
67049,02 |
700,64 |
Расчет теплоемкости жидкости. Наиболее простыми способами расчета теплоемкости жидкости являются аддитивно-групповые методы и методы, основанные на принципе соответственных состояний [4]. Аддитивно-групповые методы весьма точны при условии, что для рассматриваемого вещества известны все групповые составляющие. Для кремнийорганических соединений определение групповых составляющих ранее никем не проводилось, что делает аддитивные методы неприменимыми.
Алексеев с сотрудниками [1] предложили неаддитивный метод расчета теплоемкости жидких органохлорсиланов. Считая, что зависимость теплоемкости жидкости большинства кремнийорганических соединений при приведенных температурах менее 0,9 близка к линейной, в работе [1] было предложено следующее уравнение:
![]() (3)
(3)
где ![]() – теплоемкость жидкости, кДж/кг.К;
– теплоемкость жидкости, кДж/кг.К;
Т – температура, К;
М – молекулярная масса, г/моль;
![]() – коэффициент, равный –0,1 для
хлорсиланов и 0,74 для оксихлорсиланов;
– коэффициент, равный –0,1 для
хлорсиланов и 0,74 для оксихлорсиланов;
![]() – коэффициент, равный 18,0 для
хлорсиланов и 15,5 для оксихлорсиланов.
– коэффициент, равный 18,0 для
хлорсиланов и 15,5 для оксихлорсиланов.
Проверка показала, что данное уравнение имеет низкую точность расчета (табл. 4). Погрешность расчета теплоемкости жидкости составляет в среднем около 20% при приведенной температуре 0,55 и для большинства рассмотренных веществ увеличивается с ростом температуры. Примечательно, что в таблицах свойств, опубликованных авторами [1], для метилхлорсиланов с одним атомом кремния значения теплоемкости жидкости незначительно отличаются от данных [5] и не соответствуют результатам расчета по уравнению (3). Вероятно, уравнение (3) применимо для полиорганосилоксанов, но для более низкомолекулярных соединений (например, метилхлорсиланов) возможность его применения вызывает сомнения.
Таблица 4
Погрешность(*) расчета теплоемкости жидких кремнийорганических соединений
|
соединение |
приведенная температура |
|||||
|
0,55 |
0,7 |
0,85 |
0,55 |
0,7 |
0,85 |
|
|
погрешность по Алексееву (уравнение (3), [1]) |
погрешность по Роулинсону—Бонди (уравнение (4), [4]) |
|||||
|
дихлорсилан |
–26,9 |
–29,0 |
–24,8 |
+16,9 |
+20,7 |
+22,3 |
|
трихлорсилан |
–48,5 |
–58,4 |
–58,2 |
+1,4 |
+7,1 |
+9,9 |
|
тетрахлорсилан |
–48,8 |
–75,7 |
–100,9 |
+1,4 |
–0,6 |
–8,0 |
|
метилтрихлорсилан |
–22,7 |
–36,9 |
–45,6 |
+7,3 |
+8,0 |
+6,4 |
|
метилдихлорсилан |
–23,7 |
–19,1 |
–16,5 |
–1,3 |
+10,6 |
+13,8 |
|
диметилдихлорсилан |
–13,4 |
–14,0 |
–10,4 |
+1,4 |
+9,4 |
+14,4 |
|
диметилхлорсилан |
–1,5 |
–6,7 |
–11,0 |
+8,1 |
+7,6 |
+2,7 |
|
триметилхлорсилан |
+1,8 |
+4,0 |
+9,0 |
–5,2 |
+3,4 |
+9,6 |
|
тетраметилсилан |
+20,1 |
+15,4 |
+12,1 |
+0,1 |
–1,3 |
–6,0 |
|
гексаметилдисилоксан |
–1,3 |
–4,7 |
–6,3 |
+2,6 |
+2,1 |
+0,3 |
(*) Погрешность = [(эксп. – расч.)/ эксп.] × 100%
К неаддитивным методам также относятся методы, основанные на принципе соответственных состояний. Погрешность расчета теплоемкости жидкости данными методами обычно составляет порядка 5–10%. Наиболее простым и удобным из данных методов является расчет по модифицированному уравнению Роулинсона—Бонди ([4], формула 5.8.2):
![]() (4)
(4)
где ![]() – теплоемкость жидкости, кал/моль.К
– теплоемкость жидкости, кал/моль.К
![]() – теплоемкость газа, кал/моль.К;
– теплоемкость газа, кал/моль.К;
R – универсальная газовая постоянная, кал/моль.К;
ω – фактор ацентричности;
Tr
– приведенная температура ![]() ;
;
Tc – критическая температура, К.
Проверка этого уравнения для метилхлорсиланов с известными теплоемкостями жидкости и газа показала (табл. 4), что метод имеет удовлетворительную точность в интервале приведенных температур ниже 0,7 (для большинства рассмотренных веществ погрешность менее 10%). В интервале приведенных температур от 0,7 до 0,85 погрешность расчета возрастает. При приведенных температурах выше 0,85–0,9 погрешность превышает 10%, поэтому уравнение Роулинсона–Бонди нами не рекомендуется использовать в этих условиях.
С помощью уравнения (4) нами была впервые рассчитана температурная зависимость теплоемкости жидкости некоторых высококипящих кремнийорганических соединений, образующихся в ходе прямого синтеза метилхлорсиланов. Полученные данные аппроксимировались с помощью уравнения (5).
![]() , Дж/кмоль.К (5)
, Дж/кмоль.К (5)
Коэффициенты уравнения (5) приведены в таблице 5.
Таблица 5
Коэффициенты уравнения (5) для расчета теплоемкости жидких высококипящих продуктов прямого синтеза метилхлорсиланов (Дж/кмоль.К)
|
вещество |
интервал применимости, К |
коэффициенты уравнения (5) |
|||||
|
min |
max |
A |
B |
С |
D |
E |
|
|
Me3Si–SiClMe2 |
273 |
520 |
7,7282e005 |
-6,1936e003 |
27,0782 |
-0,0500 |
3,4674e-005 |
|
Cl3Si–O–SiCl3 |
273 |
520 |
7,5908e005 |
-6,1763e003 |
26,1619 |
-0,0484 |
3,3516e-005 |
|
Me2ClSi–O–SiClMe2 |
273 |
520 |
7,8023e005 |
-6,2883e003 |
27,5287 |
-0,0510 |
3,5422e-005 |
|
MeCl2Si–O–SiCl2Me |
273 |
525 |
7,3357e005 |
-5,7777e003 |
24,7443 |
-0,0454 |
3,1241e-005 |
|
Me3Si–SiCl2Me |
273 |
530 |
7,2303e005 |
-5,5816e003 |
24,0008 |
-0,0437 |
2,9941e-005 |
|
Me2ClSi–SiCl2Me |
273 |
535 |
7,0708e005 |
-5,4066e003 |
22,9646 |
-0,0417 |
2,8390e-005 |
|
(SiCl3)2 |
273 |
540 |
6,7348e005 |
-5,1225e003 |
21,0672 |
-0,0380 |
2,5740e-005 |
|
Me2ClSi–SiClMe2 |
273 |
535 |
7,0111e005 |
-5,3042e003 |
22,7233 |
-0,0412 |
2,8002e-005 |
|
Me2ClSi–O–SiCl2Me |
273 |
530 |
7,1354e005 |
-5,4805e003 |
23,5772 |
-0,0430 |
2,9401e-005 |
|
MeCl2Si–SiCl2Me |
273 |
545 |
6,5853e005 |
-4,8314e003 |
20,1171 |
-0,0360 |
2,4172e-005 |
|
Me3Si–CH2–SiClMe2 |
273 |
535 |
7,2001e005 |
-5,2438e003 |
22,8899 |
-0,0414 |
2,8069e-005 |
|
Me3Si–CH2–SiCl2Me |
273 |
550 |
6,7470e005 |
-4,6976e003 |
20,1609 |
-0,0360 |
2,4022e-005 |
|
Me2ClSi–CH2–SiClMe2 |
273 |
565 |
6,2603e005 |
-4,0827e003 |
17,3689 |
-0,0304 |
1,9950e-005 |
|
Me2ClSi–CH2–SiCl2Me |
273 |
580 |
5,8933e005 |
-3,6559e003 |
15,2371 |
-0,0263 |
1,6958e-005 |
|
MeCl2Si–CH2–SiCl2Me |
273 |
585 |
5,7570e005 |
-3,5290e003 |
14,4721 |
-0,0248 |
1,5944e-005 |
|
(SiCl3)2SiCl2 |
273 |
595 |
6,5122e005 |
-3,7492e003 |
14,4549 |
-0,0244 |
1,5499e-005 |
Выводы
Выполнена проверка применимости известных методов расчета теплоемкости жидкости и пара к определению свойств метилхлорсиланов. Показано, что в случае отсутствия экспериментальных данных по температурной зависимости теплоемкости метилхлорсиланов известные методы расчета могут быть использованы для прогнозирования необходимых свойств для соединений данного класса.
Для аддитивного расчета теплоемкости идеального газа метилхлорсиланов рассчитаны ранее не известные значения вкладов составляющих связей.
Впервые определены коэффициенты температурной зависимости теплоемкости жидкости и пара для высококипящих продуктов прямого синтеза метилхлорсиланов.
Рецензенты:Гартман Т.Н., д.т.н., профессор, РХТУ им. Д.И. Менделеева, зав. кафедрой информатики и компьютерного проектирования, г. Москва;
Щербакова Г.И., д.х.н., ведущий научный сотрудник лаборатории 4, ФГУП «ГНИИХТЭОС», г. Москва.



