Не теряя общности, рассмотрим цепь вида:
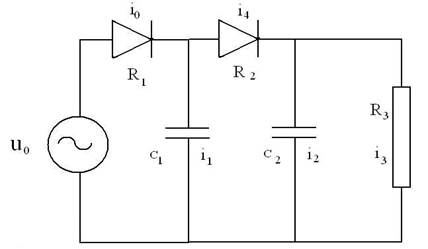
Рис. 1. Электрическая цепь с двумя диодами и двумя конденсаторами
где Ri(i = 1,2,3) – сопротивление элементов цепи,
Сi(i = 1,2) – конденсаторы постоянной емкости,
ij(j = 0,4) – величины токов на соответствующих участках цепи,
Vj (j = 1,2) – величина напряжения на соответствующем диоде,
u(t) – электродвижущая сила источника.
В этом случае имеет место следующий нелинейный вариант закона Ома:
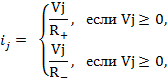(1)
где R+ и R- – различные положительные постоянные, соответствующие электрическому сопротивлению диода при протекании через него переменного тока в прямом и обратном направлениях соответственно.
Исследование математической модели для электрической цепи, содержащей два диода и два конденсатора, представляющую собой систему нелинейных дифференциальных уравнений, было проведено в статье [4].
Запишем систему дифференциальных уравнений для напряжений на конденсаторах в электрических цепях для случая, когда в электрической цепи соединены два диода и два конденсатора по схеме, представленной на рисунке 1 [2],
(2)
или в векторной форме:
(3)
Обозначим через αi значение 1/Ri, i=1, 2,3.
В качестве уравнений сравнения выберем уравнения вида:
(4)
или в векторной форме:
(5)
Тогда систему уравнений (2) можно записать в виде:
(6)
Обозначим оценки компонент вектор-функции так:
(7)
Запишем фундаментальную матрицу решений системы (4):
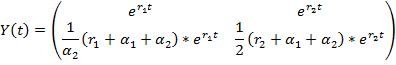(8)
и обратную к ней:
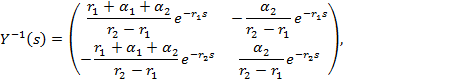(9)
где:
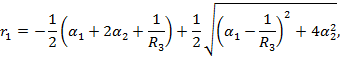
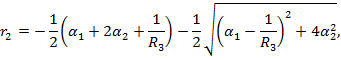
причем 
Рассмотрим случай, когда напряжение источника 
представляет собой затухающий колебательный процесс, то есть, будем считать, что 
при 
. Используем результаты статей [3, 5].
Определим для уравнений (2) и (4) множества N и 
. Очевидно, что 
Из (7) видно, что
и 
зависят от 
, поэтому в качестве выбираем 
.
Пусть функции сравнения выбраны так:
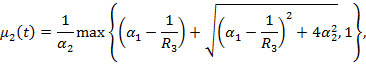(10)
тогда 
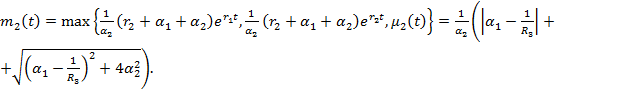(11)
Теорема. Если функция 
удовлетворяет условиям:
1. Пусть интеграл:
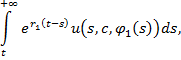(12)
где 
сходится;
2. Все решения уравнения:
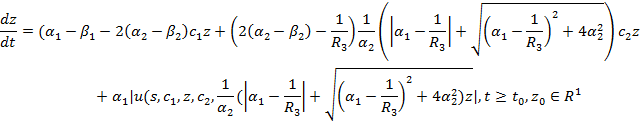
ограничены, то уравнения (2) и (4) покомпонентно асимптотически эквивалентны по Брауеру относительно функций 
, при 
+
Доказательство. Воспользуемся теоремой 1.1.5 [1]. Проверим условие:
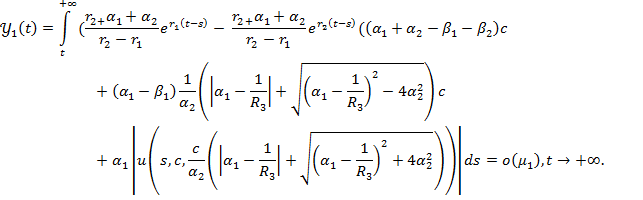
Это условие будет выполнено, если
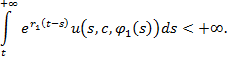
Все элементы фундаментальной матрицы ограничены, т.е.
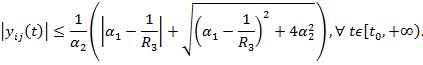
Тогда по теореме 1.1.5 [1] уравнения (2) и (4) покомпонентно асимптотически эквивалентны по Брауеру относительно функций 
, что и требовалось доказать.
Рассмотрим случай, когда напряжение источника лишь только ограниченная функция, то есть 
Зафиксируем начальный момент времени 
Будем считать, что при 
, 
Найдем оценку для решений, удовлетворяющих начальными условиями , 
.
Пусть X – банахово пространство всех ограниченных и непрерывных вектор-функций, определенных на множестве 
.
Рассмотрим шар 
и оператор:
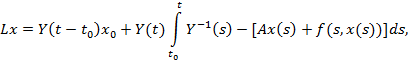(13)
где 
и 
– фундаментальная матрица решения и обратная к ней. Для компонент вектор-функции – 
справеливы оценки (6) 
Тогда имеем:
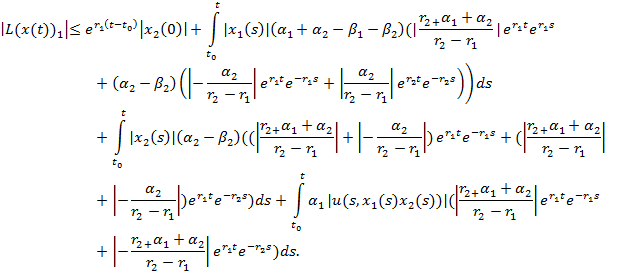(14)
Принимая во внимание, что 
неравенство примет вид:
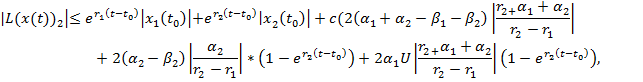
или
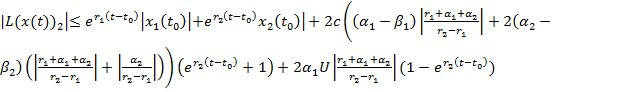. (15)
Для второй компоненты оператора L справедлива оценка вида:
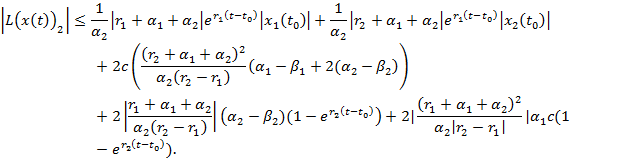(16)
Положим, что 
. Тогда оператор 
будет оператором, отображающим шар в шар, то есть 
, если будет выполнены условия:
(17)
Заменим в (17) выражение для 
через 
, получим:
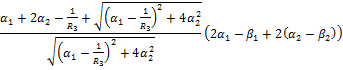
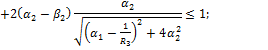(18)
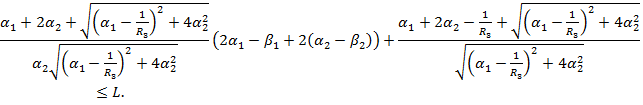
Таким образом, c учетом (18), для оператора 
при фиксированном
выполняются все условия принципа Шаудера о неподвижной точке, то есть 
Поэтому справедлива оценка для 
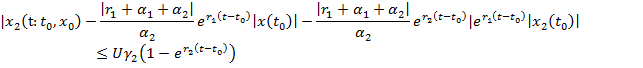(19)
при 
где 
левые части неравенства (18).
Из оценок (19) можно сделать вывод: если элементы электрической цепи подбирать так, чтобы выполнялось соотношение (18), то падение напряжения на конденсаторах не будет превосходить величины напряжения источника U.
Рецензенты:
Денисов Б. Н., д.ф.-м.н., профессор кафедры радиотехники Мордовского государственного университета им. Н.П. Огарева, г. Саранск;
Щенников В. Н., д.ф.-м.н., профессор кафедры прикладной математики, дифференциальных уравнений и теоретической механики Мордовского государственного университета им. Н. П. Огарева, г. Саранск.