Спектральные задачи с входящими параметрами в краевые условия возникают при решении многих прикладных задач математической физики [2-4, 8]. В соответствующих обратных задачах восстанавливаются неизвестные коэффициенты в уравнении и краевых условиях [5, 7, 9, 10]. Близкая по результатам работа [1] была посвящена восстановлению трех масс, сосредоточенных на тупиковых концах струнного графа с упругим закреплением, по 7 значениям собственных частот. В [6] рассматривается задача идентификации 6 параметров закрепления графа по 6 собственным значениям, однако при использовании такого же числа собственных значений решение оказывается неединственным. В данной статье в отличие от описанных выше работ восстанавливаются 3 параметра закрепления графа. Показывается единственность идентификации этих параметров по 6 собственным значениям.
Постановка обратной задачи. Рассмотрим граф ![]() в виде звезды из трех ребер-струн с одной общей вершиной графа в нуле (точка О). Длина
в виде звезды из трех ребер-струн с одной общей вершиной графа в нуле (точка О). Длина ![]() -й струны равна
-й струны равна ![]() , толщина струн одинаковая. Все три тупиковых вершины графа упруго закреплены. Каждая из струн может быть закреплена пружинками неодинаковой жесткости
, толщина струн одинаковая. Все три тупиковых вершины графа упруго закреплены. Каждая из струн может быть закреплена пружинками неодинаковой жесткости ![]()
![]() . В местах закрепления подвешены сосредоточенные массы
. В местах закрепления подвешены сосредоточенные массы ![]() . Известны также первые 6 собственных частот свободных колебаний графа
. Известны также первые 6 собственных частот свободных колебаний графа ![]() . Требуется найти жесткости пружинок
. Требуется найти жесткости пружинок ![]()
![]() .
.
На каждом ребре графа G уравнение для собственных функций и частот имеет вид
![]() ,
, ![]() ,
, ![]() (1)
(1)
Здесь мы используем в качестве аргумента ![]() расстояние от общего узла по оси OXi,
расстояние от общего узла по оси OXi, ![]() ,
, ![]() (
(![]() ) – прогибы (отклонения от состояния равновесия)
) – прогибы (отклонения от состояния равновесия) ![]() -ой струны, то есть вертикальные смещения c выходом из плоскости начального расположения струнного графа, а
-ой струны, то есть вертикальные смещения c выходом из плоскости начального расположения струнного графа, а ![]() – спектральный параметр.
– спектральный параметр.
Считаем, что общая точка O (![]() , i = 1, 2,…,n) не закреплена каким-либо образом, а является свободной (подвижной).
, i = 1, 2,…,n) не закреплена каким-либо образом, а является свободной (подвижной).
Условия в общей точке имеют вид :
![]() (2)
(2)
![]() (3)
(3)
Краевые условия
![]() ,
, ![]() (4)
(4)
Условию (2) соответствуют условия непрерывности, условию (3) – баланс сил действующих на общую вершину графа (точку О – узел) со стороны каждой из примыкающих к узлу ребер, условия (4) – условия упругого закрепления ребер (струн) с сосредоточенными массами, где ![]() – коэффициент жесткости пружины упругого закрепления
– коэффициент жесткости пружины упругого закрепления ![]() -ой вершины ребра,
-ой вершины ребра, ![]() – сосредоточенная масса, прикрепленная к
– сосредоточенная масса, прикрепленная к ![]() -ой вершине графа.
-ой вершине графа.
В терминах введенных обозначений задачу можно сформулировать следующим образом.
Постановка задачи: Пусть ![]() – неизвестны, а
– неизвестны, а ![]() – известны и попарно различны, длины струн
– известны и попарно различны, длины струн ![]() попарно одинаковы и равны единице. Требуется найти
попарно одинаковы и равны единице. Требуется найти ![]() по известному набору собственных значений
по известному набору собственных значений ![]() задачи (1)-(4).
задачи (1)-(4).
Перед решением этой обратной задачи напомним, как решается прямая задача нахождения собственных значений.
Решением уравнения (1) является следующая функция
![]() (5)
(5)
Выведем уравнение для вычисления собственных значений ![]()
![]() задачи (1) – (4).
задачи (1) – (4).
Из (2) и (3) получаем ![]() ,
, ![]() . Отсюда и
. Отсюда и
из (4) следует, что ![]()
где ![]() ;
; ![]() . Откуда
. Откуда
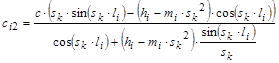 .
.
Знаменатель не обращается в нуль. Поэтому уравнение для вычисления собственных значений задачи (1) – (4) имеет следующий вид:
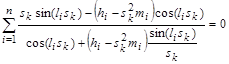 ,
, ![]() . (6)
. (6)
Вернемся теперь к обратной задаче. Уравнение (6) представляют собой систему бесконечного числа нелинейных уравнений с ![]() неизвестными
неизвестными ![]() (в нашем случае три неизвестных, т.к.
(в нашем случае три неизвестных, т.к. ![]() ). Если все длины струн
). Если все длины струн ![]() равны
равны ![]() , то будет ровно
, то будет ровно ![]() наборов решений (в нашем случае
наборов решений (в нашем случае ![]() ).
).
Возникает вопрос: какое конечное число собственных значений нужно знать для однозначной идентификации трех закреплений графа?
Для того чтобы ответить на поставленный вопрос, сведем (6) к системе линейных уравнений. Для этого приведем (6) к общему знаменателю. Нули числителя этой дроби и есть собственные значения задачи (1)-(4). Следовательно, собственные значения задачи (1)-(4) удовлетворяют следующему уравнению (числитель суммы (6) равен нулю):
![]() (7)
(7)
где ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;![]()
![]()
![]() ; (8)
; (8)
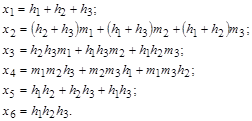 (9)
(9)
Пусть ![]() собственные значения задачи (1)-(4) подставим их в (7). В результате получим систему шести линейных уравнений от шести неизвестных
собственные значения задачи (1)-(4) подставим их в (7). В результате получим систему шести линейных уравнений от шести неизвестных ![]() :
:
![]() ,
, ![]() (10)
(10)
Из правил Крамера следует, что если определитель матрицы
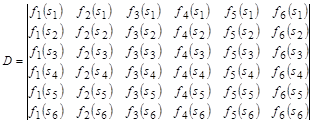 (11)
(11)
системы уравнений (10) отличен от нуля, то неизвестные![]() находятся единственным образом по формулам
находятся единственным образом по формулам ![]()
![]() , где
, где ![]() - определитель матрицы, получаемый заменой
- определитель матрицы, получаемый заменой ![]() -ого столбца столбцом свободных членов.
-ого столбца столбцом свободных членов.
Справедлива следующая теорема.
Теорема 1. Если ![]() являются точными собственными значениями краевой задачи (1)-(4),
являются точными собственными значениями краевой задачи (1)-(4), ![]() и значения сосредоточенных масс попарно различны, т.е. удовлетворяют условию
и значения сосредоточенных масс попарно различны, т.е. удовлетворяют условию ![]() , то система (10) имеет единственное решение
, то система (10) имеет единственное решение ![]() , определяемое по формулам Крамера
, определяемое по формулам Крамера ![]()
![]() , а значения коэффициентов жесткости пружинок
, а значения коэффициентов жесткости пружинок ![]() ,
, ![]() ,
, ![]() находятся однозначно по формулам (9).
находятся однозначно по формулам (9).
Доказательство:
Согласно правилу Крамера, если определитель матрицы (11), системы уравнений (10) отличен от нуля. Поэтому неизвестные ![]() находятся единственным образом по формулам
находятся единственным образом по формулам ![]()
![]() , где
, где ![]() - определитель, получаемый из определителя
- определитель, получаемый из определителя ![]() заменой
заменой ![]() -ого столбца столбцом свободных членов. Покажем теперь, что значения коэффициентов жесткости пружинок
-ого столбца столбцом свободных членов. Покажем теперь, что значения коэффициентов жесткости пружинок ![]() ,
, ![]() ,
, ![]() также находятся однозначно.
также находятся однозначно.
Допустим наряду с решением ![]() ,
, ![]() ,
, ![]() существует
существует ![]() ,
, ![]() ,
, ![]() . Система (10) имеет единственное решение {
. Система (10) имеет единственное решение {![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() }. Поэтому (9) можно записать в следующем виде:
}. Поэтому (9) можно записать в следующем виде:
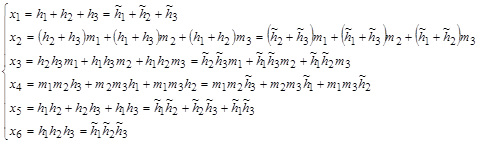
Имеем, из трех уравнений системы (9) (содержащих только ![]() ) 6 наборов решений, и, учитывая наше допущение,
) 6 наборов решений, и, учитывая наше допущение, 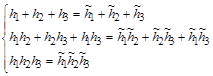
![]() будут следующие 3! наборов решений:{
будут следующие 3! наборов решений:{![]() ,
,![]() ,
, ![]() }; {
}; {![]() ,
, ![]() ,
, ![]() }; {
}; {![]() ,
,![]() ,
,![]() }, {
}, {![]() ,
,![]() ,
,![]() }; {
}; {![]() ,
, ![]() ,
, ![]() };{
};{![]() ,
, ![]() ,
, ![]() }
}
Но в системе (9) есть еще три уравнения 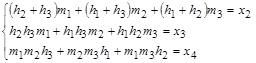 .
.
Проверим все ли наборы решений удовлетворяют этим трем уравнениям системы (9). Например, ![]() ,
, ![]() ,
, ![]() . Получили 1)
. Получили 1) ![]() или
или ![]() ;2)
;2) ![]() или
или ![]() или
или ![]() ; 3)
; 3) ![]() или
или ![]() или
или ![]() . Т.е. если
. Т.е. если ![]() , то
, то ![]() . А это противоречит условию теоремы, согласно которому
. А это противоречит условию теоремы, согласно которому ![]() . Аналогичная ситуация при следующих наборах решений. Т.е. если наряду с решением
. Аналогичная ситуация при следующих наборах решений. Т.е. если наряду с решением ![]() ,
, ![]() ,
, ![]() существует решение
существует решение ![]() ,
, ![]() ,
, ![]() , то
, то ![]() ,
, ![]() ,
, ![]() . Из шести наборов решений последним трем уравнениям удовлетворяет только первый набор решений, в котором тройки
. Из шести наборов решений последним трем уравнениям удовлетворяет только первый набор решений, в котором тройки ![]() ,
, ![]() ,
, ![]() и
и ![]() ,
, ![]() ,
, ![]() совпадают. Таким образом, при решении обратной задачи на восстановление значений коэффициентов жесткости получаем однозначное решение.
совпадают. Таким образом, при решении обратной задачи на восстановление значений коэффициентов жесткости получаем однозначное решение.
Пример 1. Пусть шесть собственных значения задачи (1)-(4) есть следующие значения: ![]() =0.9419374665,
=0.9419374665, ![]() =1.673848777,
=1.673848777, ![]() =1.876338247,
=1.876338247, ![]() =2.635099364,
=2.635099364, ![]() =3.758863968,
=3.758863968, ![]() = 5.146231313 и известны
= 5.146231313 и известны ![]() (
(![]() ) попарно различны, т.е. удовлетворяют условию:
) попарно различны, т.е. удовлетворяют условию:![]()
![]() ,
, ![]() ,
, ![]() . Требуется найти
. Требуется найти ![]() ,
, ![]() ,
, ![]() .
.
Воспользовавшись системой линейных уравнений (10) по формулам Крамера, получим однозначно ![]() 5.99999997752987,
5.99999997752987, ![]() 5.80000000289103,
5.80000000289103, ![]() 5.10000002458480,
5.10000002458480, ![]() 1.38000000224032,
1.38000000224032, ![]() 11.0000000050655,
11.0000000050655, ![]() 6.00000000977745. Используя формулы (9) коэффициенты жесткости пружинок равны
6.00000000977745. Используя формулы (9) коэффициенты жесткости пружинок равны ![]() 1.00000001341475,
1.00000001341475, ![]() 1.99999991188333,
1.99999991188333, ![]() 3.00000009681947
3.00000009681947
Теорема (устойчивости решения). Если для любого положительного числа ![]() , существуют
, существуют ![]() , такое что
, такое что ![]()
![]() , тогда выполняется неравенство
, тогда выполняется неравенство ![]()
![]() . Эта теорема следует из аналитичности
. Эта теорема следует из аналитичности ![]() и
и ![]() .
.
Предложение 1. Если константы краевой задачи (1)-(4) одинаковы ![]() (
(![]() =1,2,3), тогда константы
=1,2,3), тогда константы ![]() (
(![]() =1,2,3) в граничных условиях задачи (1)-(4) находятся с точностью до перестановок
=1,2,3) в граничных условиях задачи (1)-(4) находятся с точностью до перестановок ![]() (
(![]() =1,2,3) местами.
=1,2,3) местами.
Пример 2. Пусть известен следующий набор собственных значений ![]() =0.9309993125,
=0.9309993125, ![]() =1.6259086984,
=1.6259086984, ![]() = 1.9149805237. Известны значения сосредоточенных масс
= 1.9149805237. Известны значения сосредоточенных масс ![]() =0.5 (
=0.5 (![]() =1,2,3). Требуется найти значения коэффициенты жесткости
=1,2,3). Требуется найти значения коэффициенты жесткости ![]() (
(![]() =1,2,3). Подставив известные значения в (8, 9, 10, 11), получим:{
=1,2,3). Подставив известные значения в (8, 9, 10, 11), получим:{![]() = 1.00000,
= 1.00000, ![]() = 1.99999,
= 1.99999, ![]() = 3.00000},{
= 3.00000},{![]() = 1.00000,
= 1.00000, ![]() = 3.00000,
= 3.00000, ![]() = 1.99999},{
= 1.99999},{![]() = 1.99999,
= 1.99999, ![]() = 1.00000,
= 1.00000, ![]() = 3.00000},{
= 3.00000},{![]() = 1.99999,
= 1.99999, ![]() = 3.00000,
= 3.00000, ![]() = 1.00000},{
= 1.00000},{![]() = 3.00000,
= 3.00000, ![]() = 1.00000,
= 1.00000, ![]() = 1.99999},{
= 1.99999},{![]() = 3.00000,
= 3.00000, ![]() = 1.99999,
= 1.99999, ![]() = 1.00000}.
= 1.00000}.
Предложение 2. Если константы краевой задачи (1)-(4) одинаковы![]() (
(![]() =1,2,3), тогда константы
=1,2,3), тогда константы ![]() (
(![]() =1,2,3) в граничных условиях задачи (1)-(4) находятся с точностью до перестановок
=1,2,3) в граничных условиях задачи (1)-(4) находятся с точностью до перестановок![]() (
(![]() =1,2,3) местами.
=1,2,3) местами.
Таким образом, в настоящей работе показано, что для однозначной идентификации коэффициентов жесткости пружины ![]()
![]() по собственным значениям колебаний графа и известному набору сосредоточенных трех масс
по собственным значениям колебаний графа и известному набору сосредоточенных трех масс ![]() – достаточно использование шести собственных значений. Для решения задачи предложен метод дополнительных неизвестных.
– достаточно использование шести собственных значений. Для решения задачи предложен метод дополнительных неизвестных.
Выявлено, что если сосредоточенные массы попарно различны, то коэффициенты жесткости пружинок находятся единственным образом. Если значения сосредоточенных масс одинаковы, то коэффициенты жесткости пружинок находятся с точностью до перестановок их местами.
Полученные результаты важны для конструирования виброзащитных систем, а также для диагностики таких систем.
Рецензенты:
Спивак С.И., д.ф.-м.н., профессор, заведующий кафедрой математического моделирования. Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Башкирский государственный университет», г. Уфа;
Султанаев Я.Т., д.ф.-м.н., профессор, главный научный сотрудник лаборатории «Механика твердого тела». Федеральное государственное бюджетное учреждение науки Институт механики им. Р.Р. Мавлютова Уфимского научного центра Российской академии, г. Уфа.



