Непосредственные преобразователи электрической энергии (НПЭ) находят широкое применение для управления механическими параметрами электромеханических преобразователей (скорость и момент), мощностью в технических объектах (освещение, тепловые процессы), напряжениями и токами (гальванотехника), потоками реактивной мощности, для определения качественных показателей электрических машин [1 – 7]. Решение актуальной задачи математического моделирования НПЭ на базе существующих подходов затруднено факторами, связанными с использованием множества различных структур и большим числом задаваемых параметров. Такие подходы с моделированием каждого переключающего элемента (ПЭ) требуют задания множества возможных состояний каждого из ПЭ. Количество структур зависит от структуры силовой части и от алгоритма управления. В работе рассмотрены математическое моделирование НПЭ и алгоритм моделирования выходного напряжения, основанные на использовании предложенного авторами метода, который заключается в представлении выходного напряжения НПЭ в виде единственного гармонического колебания с дискретно управляемой начальной фазой [2].

На рис. 1 представлена структура преобразования параметров электрической энергии (напряжения U, частоты ω, фазового сдвига φ и количества фаз входного m и выходного n напряжения).

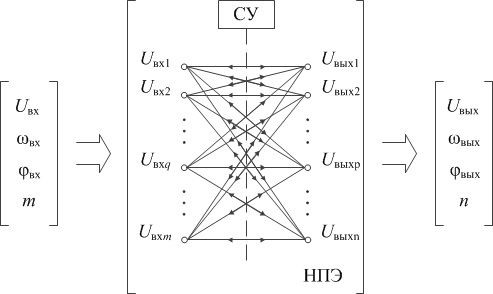
Рис. 1. Структура непосредственного преобразования параметров электрической энергии

При непрерывном режиме работы число возможных состояний НПЭ определяется выражением:

(1)

где:

m – число входных фаз;

n – число выходных фаз;

k – минимально возможное число фаз выходного напряжения.

Система входных напряжений, поступающих на вход НПЭ, включает m фаз

Ui(ωВХt) = Um sin(ωВХt – φi), (2)

где:

Ui(ωВХt) – мгновенное значение входного напряжения;

Um – амплитудное значение входного напряжения;

ωВХ – круговая частота;

φi – фазовый сдвиг.

К выходу НПЭ с раздельным управлением в каждый момент времени подключается только одна из множества ЭДС, поступающих на вход. На выходе НПЭ формируется напряжение с амплитудным и мгновенным значениями Um2 и Ui(ωВЫХt), фазовым сдвигом φi, количеством фаз n и круговой частотой ωВЫХ.

Зададим гармоническое колебание с дискретно управляемой начальной фазой:

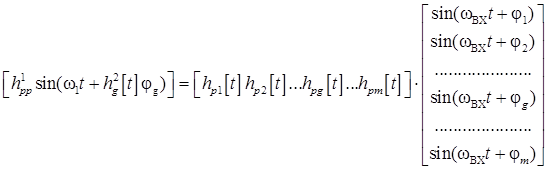(3)

Следующая система уравнений задаёт процедуру непосредственного преобразования электрической энергии n‑фазного НПЭ с раздельным управлением:

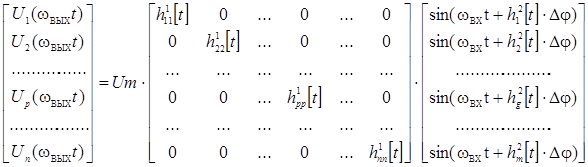(4)

Возможные способы управления НПЭ предлагается задать переключающими функциями:

;
, (5)

где:

l = 2·kf·π/Δϕ -1 = kf·m – 1;

kf = ωВХ/ωВЫХ – коэффициент преобразования частоты;

Ni – коэффициент, определяемый соотношением амплитуд различных полуволн выходного напряжения;

ni – коэффициент, определяющий фазовое положение полуволны входного напряжения в выходном напряжении.

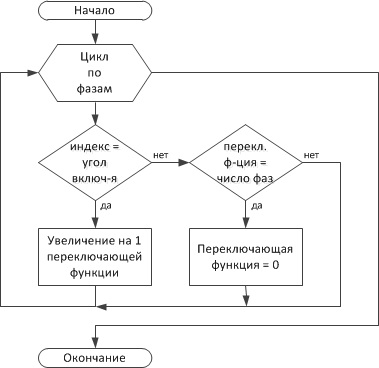
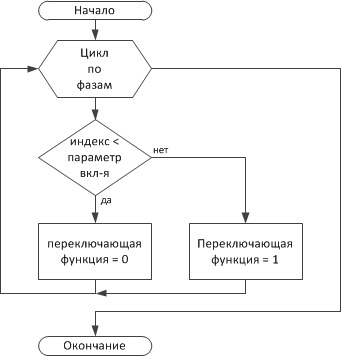
Блок-схемы алгоритмов формирования кривых выходного напряжения НПЭ отражены на рис. 2 и рис. 3.

 а)

 б)

Рис. 2. Изменение переключающих функций а) начальной фазы
и б) амплитуды

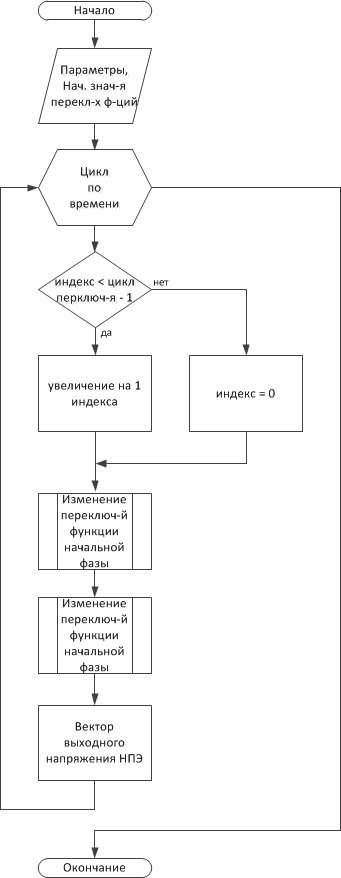
Рис. 3. Основной цикл

На рис. 4 показан фрагмент листинга программы моделирования в системе Mathcad, содержащий определение начальных значений, закона изменения переключающих функций начальной фазы и амплитуды.

Рис. 4. Фрагмент листинга программы моделирования в системе Mathcad

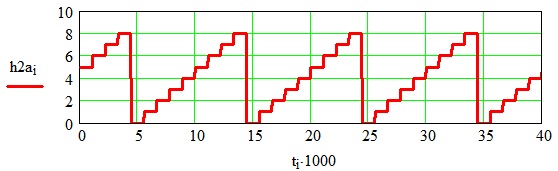
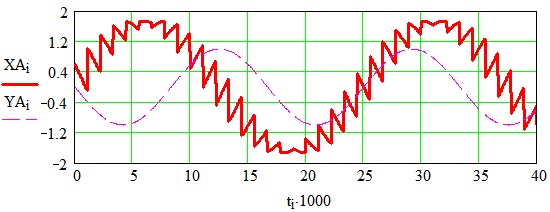
Результаты моделирования НПЭ на основе математической модели (4) и предложенного алгоритма в среде Mathcad показаны на рис. 5. Для параметров системы приняты значения: входная частота f = 60 Гц, число фаз входного напряжения m = 9, фазовый угол включения тиристоров α = 0 эл. град. На рисунке представлены: XA – выходное напряжение в фазе А, YA – выходной ток в фазе А.

 а)

 б)

Рис. 5. Результаты моделирования: а) изменение переключающей функции начальной фазы, б) выходное напряжение и ток НПЭ в фазе А (ток опережает напряжение на 90 эл. град.)

Предложены метод моделирования и алгоритм формирования выходного напряжения НПЭ на основе описания, отличающегося от известных наличием вектора синусоидального напряжения с дискретно управляемой начальной фазой и диагональной переключающей матрицы. Проведено математическое моделирование НПЭ. На базе алгоритма и метода математического моделирования возможно исследование многодвигательных многосвязных вентильно-электромеханических систем с НПЭ.

Рецензенты:

Данилов А.М., д.т.н., профессор, заведующий кафедрой математики и математического моделирования, ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза;

Косенок Ю.Н., д.т.н., доцент, начальник кафедры, Пензенский артиллерийский инженерный институт, г. Пенза.