Строительство и эксплуатация магистральных трубопроводов в условиях Крайнего Севера осложняются криогенной структурой их оснований, обусловливающей необходимость учета тепловых процессов в геотехнической системе. Вечномерзлые грунтовые основания при оттаивании теряют свою структурную устойчивость под техногенными силовыми и тепловыми нагрузками, что приводит к значительной местной просадке, появлению прогибов и потере общей устойчивости трубопроводов [4, 8-10].
Одним из принципов использования вечномерзлых грунтов в качестве среды функционирования трубопровода является допущение их возможного незначительного протаивания, не приводящего к возникновению недопустимых напряжений и деформаций в стенке трубы. Достоверный прогноз максимальной глубины протаивания за весь период эксплуатации трубопровода требует учета в расчетных методиках значимых факторов, влияющих на протекающие процессы в системе. Анализ существующих методик, оценка их преимуществ и недостатков необходима для выбора наилучшей методики применительно к исследуемому способу прокладки трубопровода.
Цель работы: обосновать выбор наиболее универсальной и достоверной методики расчета глубины протаивания мерзлого грунта под трубопроводом, позволяющей учитывать конструктивные особенности сооружения и воздействие основных факторов климатического происхождения.
Задачи:
1) провести анализ научной литературы, нормативно-технической документации Российской Федерации и обобщить сведения о типовых методиках расчета глубины протаивания вечномерзлых грунтов под трубопроводами;
2) оценить разницу в величинах глубины протаивания, рассчитанной по различным методикам для рассматриваемого способа прокладки;
3) выявить основные причины расхождения в результатах, сильные и слабые стороны анализируемых методик.
Задача о движении границы оттаивания грунта относится к весьма важному классу задач о фазовых переходах первого рода. Основной сложностью при их решении является необходимость учета скрытой теплоты при переходе из одной фазы в другую. Это приводит дифференциальное уравнение теплопроводности (1) к нелинейному виду, так как основные характеристики вещества (плотность, теплоемкость, теплопроводность) зависят от температуры:
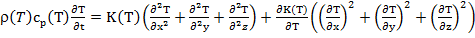 . (1)
. (1)
Одной из первых публикаций по данному вопросу была работа Йозефа Стефана [12]. В ней была решена одномерная задача об изменении толщины полярного льда. Для исследуемого способа прокладки подземного трубопровода задачу можно условно считать двухмерной, расчетная схема которой приведена на рисунке 1.
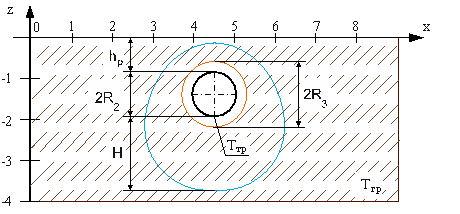
Рис. 1. Схема к определению глубины протаивания грунта под трубопроводом:
H – глубина протаивания; R2 – наружный радиус трубопровода;R3 – наружный радиус теплоизоляции; hp – глубина заложения трубопровода; Тгр– температура грунта; Ттр– температура перекачиваемого продукта
Точного решения для данной задачи до сих пор не найдено. Однако важное приближенное решение (далее по тексту – методика I) существует для осесимметричного случая и условно стационарного распределения температур. Соответственно, решение данной задачи справедливо только для случая, когда скрытая теплота плавления льда в грунте много больше его теплоемкости, а глубина заложения трубопровода такова, что можно пренебречь теплообменом с атмосферой [5]. Уравнение методики I является трансцендентным относительно H и решается численно.
Для описания стационарной зоны оттаявшего грунта под нижней образующей трубопровода может использоваться формула Форхгеймера—Гребера [1, 5-7]. Данная формула (далее — методика II) получена путем точного решения уравнения теплопроводности методом источников и стоков. Функция источника имитирует подземный трубопровод на глубине hр, а функция стока располагается симметрично относительно прямой z=0. Таким способом становится возможным удовлетворить постоянной температуре на поверхности грунта. Методика II применима в случае, если коэффициент конвективной теплоотдачи на поверхности Земли принимает очень большие значения или глубина заложения такова, что можно пренебречь повышением температуры поверхности Земли непосредственно над трубопроводом. Формула Форхгеймера—Гребера имеет большое прикладное значение, поскольку позволяет рассчитывать изменение температуры продукта по длине трубопровода, а, следовательно, и изменение величины ореола оттаивания по длине трубопровода [1, 11].
Дальнейшим развитием метода источников и стоков явилась формула, позволяющая рассчитывать ореол оттаивания под многониточными коридорами трубопроводов [3]. Основным ее недостатком является отсутствие возможности удовлетворить граничным условиям на всей поверхности трубопровода. Поэтому в дальнейшем Даниэляном Ю.С. была получена зависимость, которая позволяет задавать температуру поверхности трубопровода в нескольких точках [2]. Устремляя количество точек к бесконечности, можно полностью удовлетворить граничным условиям на поверхности трубопровода.
В работе Быкова Л.И. и Мустафина Ф.М. приводится выражение (далее — методика III), позволяющее рассчитать глубину протаивания под нижней образующей трубопровода в динамике при использовании кольцевого теплоизоляционного экрана с различными углами охвата наружной поверхности трубопровода [1]. Уравнение методики III является трансцендентным относительно H и решается численно.
В РД 39-0147323-604-86 «Инструкция по теплотехническим расчетам при проектировании нефтяных промыслов» для выполнения теплотехнических расчетов при проектировании нефтяных промыслов приводится выражение (далее – методика IV), позволяющее оценить динамику глубины протаивания грунта под подземными трубопроводами без теплоизоляции.
Среди способов решения задачи о расчете глубины протаивания особое место занимает стремительно развивающаяся методика прямого решения нелинейного дифференциального уравнения теплопроводности (1) при граничных условиях (2) методами конечных элементов или конечных разностей (далее по тексту – методика V):
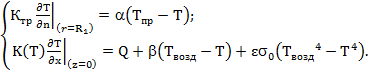 (2)
(2)
Основным преимуществом методики V является возможность учитывать при расчетах влияние таких факторов климатического происхождения, как: солнечная радиация, температура воздуха, скорость ветра, толщина снежного покрова, излучение атмосферы и подстилающей поверхности грунта в инфракрасной области спектра.
Основные отличия методик I – V, их преимущества и недостатки сведены в таблице 1.
Из таблицы 1 становится видно, что методика V имеет лишь один недостаток — потребность в больших вычислительных ресурсах. В настоящее время эта проблема уже не стоит так остро в связи со значительным прогрессом в области увеличения производительности электронно-вычислительных машин. В то же время эта методика обладает достаточной универсальностью для проведения сложных расчетов теплового взаимодействия горячих трубопроводов с многолетнемерлыми грунтами и прилегающими сооружениями.
Таблица 1
Основные параметры сравнения методик I-V
|
Методика
Параметр сравнения |
Методика I |
Методика II |
Методика III |
Методика IV |
Методика V |
|
Граница ореола оттаивания |
Нестационарная, известна только под нижней образующей трубопровода |
Стационарная, известна только под нижней образующей трубопровода |
Нестационарная, известна только под нижней образующей трубопровода |
Нестационарная, известна только под нижней образующей трубопровода |
Нестационарная, известна в любом направлении от трубопровода |
|
Возможность учета толщины теплоизоляционного покрытия |
да |
да |
да |
нет |
да |
|
Учет теплообмена с атмосферой |
нет |
да |
нет |
да |
Учитывает конвективный и радиационный теплообмен |
|
Учет влияния толщины снежного покрова |
нет |
да |
нет |
нет |
да |
|
Учет сезонного колебания температур |
нет |
нет |
нет |
нет |
да |
|
Учет естественного температурного поля грунта |
нет |
нет |
нет |
нет |
да |
|
Преимущества |
Относительная простота при использовании в оценочных инженерных расчетах |
Возможность расчета сложных конструкций и учета большого числа климатических факторов |
|||
|
Недостатки |
Невозможно провести расчет для сложных конструкций и учесть влияние факторов климатического происхождения |
Потребность в мощных вычислительных ресурсах |
|||
Обсуждение результатов тестовых расчетов. Поскольку приведенные выше методики имеют близкие границы применимости, было проведено 3 тестовых расчета глубины протаивания грунта под трубопроводом с различной толщиной и конструкцией теплоизоляционного покрытия и следующими основными характеристикам: ![]() мм,
мм, ![]() мм,
мм, ![]() ,
, ![]() °С. Результаты расчетов приведены на рисунках 2–4.
°С. Результаты расчетов приведены на рисунках 2–4.
Методика III, вероятно, содержит ошибку, о чем свидетельствует зависимость на рисунке 4: при а=0 град. глубина протаивания должна в точности совпадать с глубиной протаивания для нетеплоизолированного трубопровода. Однако вместо этого мы получаем стационарную глубину протаивания, которая к тому же значительно меньше, чем у теплоизолированного трубопровода.
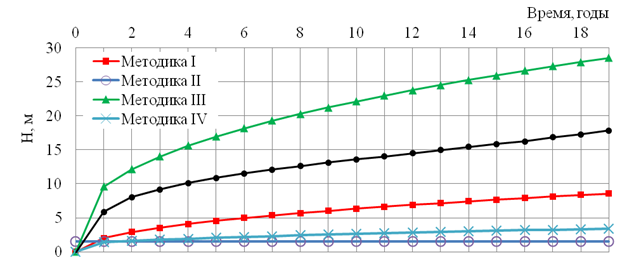
Рис. 2. Расчетная глубина протаивания под нетеплоизолированным трубопроводом
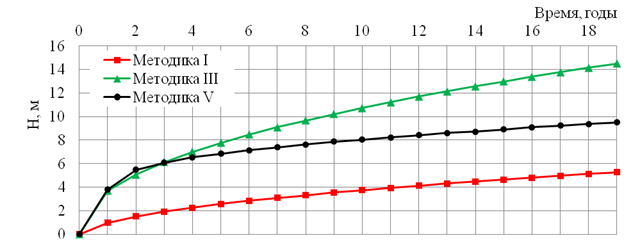
Рис. 3. Расчетная глубина протаивания под трубопроводом с кольцевой теплоизоляцией из вспененного полистирола толщиной 50 мм
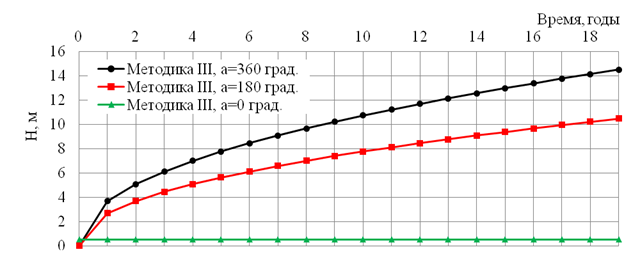
Рис. 4. Расчетная глубина протаивания под трубопроводом с теплоизоляционным экраном из вспененного полистирола толщиной 50 мм и различными углами охвата: a – угол охвата трубопровода теплоизоляцией [1]
Из рисунков 2 и 3 видно, что глубины протаивания, рассчитанные по различным методикам, различаются в несколько раз. В первую очередь это связано с различным подходом к решению уравнения (1). Немаловажную роль играет и тот факт, что каждая из методик учитывает лишь какой-то отдельно взятый климатический фактор, и лишь методика V учитывает всю их совокупность. Каждый из внешних факторов вносит в расчетную схему вклад, которым нельзя пренебрегать. Для обеспечения наибольшей точности глубину протаивания следует определять путем решения уравнения (1) методами конечных элементов или конечных разностей. Остальные методики можно использовать лишь для оценочных расчетов.
Выводы
Выполнен анализ типовых методик расчета глубин протаивания мерзлого грунта под трубопроводом. Сопоставление границ применимости анализируемых методик показало, что только методика, основанная на прямом решении дифференциального уравнения теплопроводности численными методами, обладает наибольшей универсальностью и практически не имеет ограничений в применении. Проведен тестовый расчет глубин протаивания многолетнемерзлого грунта под трубопроводом. Показана значительная разница в результатах расчетов по анализируемым методикам. На основании результатов тестовых расчетов было обосновано, что каждый из климатических факторов вносит значимый вклад в расчетную схему. Сделан вывод о необходимости учета всей совокупности климатических факторов при расчетах глубин протаивания под трубопроводами и связанной с этим необходимости решения дифференциального уравнения теплопроводности исключительно методами конечных элементов или конечных разностей.
Рецензенты:
Мерданов Ш.М., д.т.н., заведующий кафедрой «ТТС», ФГБОУ ВПО «Тюменский государственный нефтегазовый университет», г. Тюмень;
Тарасенко А.А., д.т.н., профессор кафедры «ТУР», ФГБОУ ВПО «Тюменский государственный нефтегазовый университет», г. Тюмень.



