Как известно, задача синтеза заключается в нахождении таких значений параметров моделируемой системы, которые обеспечивают ее наилучшую структуру, исследуемую с позиций операторного подхода (вход-выход) в соответствующей внешней среде.
Работа состоит из трех частей. Первая содержит некоторые сведения из теории локально ограниченных функциональных пространств (ЛОФП), являющихся внешней средой рассматриваемой системы, и свойств Hλ-операторов, введенных нами в 1990-1991 гг. [1]. Вторая часть посвящена формированию пространства информативных признаков.
Существо третьей части составляет параметрический синтез исходной системы на модельном примере интегро-степенного функционального ряда Вольтерра по критерию среднеквадратической ошибки и нахождение оптимальной оценки метода регуляризации.
1. Вспомогательные сведения
Целесообразно упомянуть [3], что выбор того или иного функционального пространства в качестве внешней среды исходной системы в ряде случаев является определяющим для конкретного метода синтеза. К настоящему времени при операторном подходе к синтезу нелинейных динамических систем (НДС) наиболее используемыми являются следующие ЛОФП.
Обозначим через ![]() +
+![]()
![]()
![]() – поле вещественных неотрицательных чисел,
– поле вещественных неотрицательных чисел, ![]() – пространство непрерывных функций, М – пространство измеримых по Лебегу функций,
– пространство непрерывных функций, М – пространство измеримых по Лебегу функций, ![]() (
(![]() )
) ![]() – пространство измеримых функций u(t) действительного аргумента
– пространство измеримых функций u(t) действительного аргумента ![]()
![]() с p-интегрируемым модулем, для которых:
с p-интегрируемым модулем, для которых:
![]() (
(![]() ) =
) = ![]()
![]() ,
, 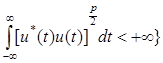 , (1)
, (1)
где ![]() – эрмитово сопряженная функция к исходной измеримой функции
– эрмитово сопряженная функция к исходной измеримой функции ![]() .
.
F-норма элемента ![]()
![]() (
(![]() ) определяется по формуле:
) определяется по формуле:
![]()
![]() (
(![]() )
) ![]() =
= ![]() ,
, ![]()
![]() +. (2)
+. (2)
В монографии [3] (c.c. 20-30) нами рассмотрен ряд конструктивных примеров локально ограниченных пространств, являющихся основой среды НДС, из которых наиболее широкой топологией обладают пространства Орлича.
Так, локально ограниченное пространство Орлича ![]() состоит из измеримых по Лебегу функций u(t), определенных на компактном множестве
состоит из измеримых по Лебегу функций u(t), определенных на компактном множестве ![]() Rn , порождаемых неотрицательной неубывающей функцией Юнга Ф, с помощью интегрального модуляра, имеющего вид
Rn , порождаемых неотрицательной неубывающей функцией Юнга Ф, с помощью интегрального модуляра, имеющего вид ![]() .
.
Обозначим через ![]() произвольную седловую функцию Юнга, через
произвольную седловую функцию Юнга, через ![]() – интегральный модуляр,
– интегральный модуляр, ![]() – локально ограниченное F-квазинормированное пространство Орлича, где
– локально ограниченное F-квазинормированное пространство Орлича, где
![]() . (3)
. (3)
Структура данного функционального пространства к настоящему времени практически не исследована, хотя решение некоторых прикладных задач в этом ЛОФП Орлича представляет существенный интерес для оценок двойственного зазора в невыпуклом программировании для случая адаптивных НДС [2].
Как уже отмечалось, исходная нелинейная система содержит Нλ-оператор, суть которого в следующем (подробнее см. [3]).
Определение 1.1. Пусть Е1 и Е2 – два ЛОФП измеримых по Лебегу функций, оператор А: Е1→М, ![]() . Назовем оператор А Нλ-оператором, если для
. Назовем оператор А Нλ-оператором, если для ![]() выполняется условие:
выполняется условие:
![]() (4)
(4)
где функция Н: ![]() +→
+→![]() + принадлежит классу F(L) (см. [1]), для каждого элемента
+ принадлежит классу F(L) (см. [1]), для каждого элемента ![]() и для любых измеримых подмножеств D1 и D2 из Ω таких, что D1
и для любых измеримых подмножеств D1 и D2 из Ω таких, что D1![]() D2= Ω и D1
D2= Ω и D1![]() D2=Ø,
D2=Ø, ![]() – индикатор множества Di, i=1,2,
– индикатор множества Di, i=1,2, ![]()
![]() .
.
Как оказалось, вышеперечисленные нелинейные интегральные операторы являются Н-операторами, подчиняющимися условию:
![]() , (5)
, (5)
где функция ![]() , для каждого элемента
, для каждого элемента ![]() и для всех попарно дизъюнктных измеримых подмножеств
и для всех попарно дизъюнктных измеримых подмножеств ![]() – индикатор подмножества
– индикатор подмножества ![]() .
.
Частными примерами Нλ-операторов А являются: оператор суперпозиции (Немыцкого), нелинейные атомические интегральные операторы Гаммерштейна, Урысона, интегро-степенные ряды Вольтерра, нормальные интегранты, локально определенные операторы.
При синтезе систем большую роль играют преобразования (операторы), входящие в модель. Примерами могут служить различные нелинейно-инерционные динамические системы для случая, когда информация о физической системе минимальна. В такого рода моделях широкое применение получили нелинейные интегральные уравнения Гаммерштейна-Урысона, интегро-степенные ряды Вольтера-Пикара с входящими в них существенно нелинейными операторами, уравнения с внутренними функциональными операторами суперпозиции (Немыцкого).
Пример 1.1. Рассмотрим систему, заданную отображением вход-выход при помощи матрицы-функции импульсной характеристики ![]() в виде
в виде
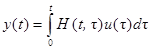 . (6)
. (6)
Для нее, как известно [1], существует реализация произвольного причинного отображения вход-выход, задаваемая уравнениями состояния вида:
![]() (7)
(7)
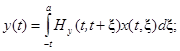
![]() (8)
(8)
В пункте 3 данной работы нами рассматривается задача синтеза системы, содержащей так называемый суперлинейный Hλ-оператор.
Определение 1.2. Оператор ![]() назовем суперлинейным, если
назовем суперлинейным, если
![]() (9)
(9)
где ![]()
![]() ,
, ![]()
![]() ,
, ![]() .
.
Примерами суперлинейных операторов являются:
1. Всякий непрерывный выпуклый функционал Г. Достаточно выбрать ![]() настолько малым, чтобы число
настолько малым, чтобы число ![]() имело одинаковый знак с
имело одинаковый знак с ![]() при
при ![]() . Тогда из выпуклости функционала Г вытекает
. Тогда из выпуклости функционала Г вытекает
![]() (10)
(10)
при всех ![]() .
.
2. Нелинейный интегральный оператор Урысона
![]() (11)
(11)
в паре F-квазинормированных пространств ![]() будет суперлинейным, если его ядро подчиняется условиям:
будет суперлинейным, если его ядро подчиняется условиям:
а) ![]() при
при ![]()
![]() .
.
b) ![]() . (12)
. (12)
3. Достаточным условием суперлинейности оператора Немыцкого ![]() , где f – нормальный интегрант (в частности, каратеодориева функция), является однородность функции f(s,u) по u при каждом s и выполнение ограничения
, где f – нормальный интегрант (в частности, каратеодориева функция), является однородность функции f(s,u) по u при каждом s и выполнение ограничения
![]() . (13)
. (13)
Для вышеуказанных систем перспективной представляется идея мажорирования операторов. Теория таких нелинейных операторов, действующих в локально невыпуклых топологических пространствах, – интересная и исключительно важная в прикладном аспекте область функционального анализа. Так, для случая произвольной пары локально ограниченных пространств измеримых функций и заданных каратеодориевых ядер К1 и К2 нами ранее в [3] показано, что при условии ![]() нелинейный интегральный оператор с ядром К1 наследует нужные «хорошие» свойства оператора, содержащего ядро К2.
нелинейный интегральный оператор с ядром К1 наследует нужные «хорошие» свойства оператора, содержащего ядро К2.
2. Пространство информативных признаков
Очевидно, что выбор совокупности диагностических признаков (так называемая задача формирования пространства информативных признаков) оказывает решающее влияние на точность распознавания технического состояния объектов диагностирования. Как известно [1], задача выбора диагностических признаков формулируется следующим образом. Пусть задано исходное пространство признаков X, размерности p. Необходимо найти преобразованное пространство Y, элементами которого являются q-мерные векторы, причем q < p. Формально такая задача заключается в определении отображения A: X →Y, которое исходному пространству Х ставит в соответствие искомое пространство Y.
Каждую реализацию вектора нагрузки на систему можно рассматривать как многомерную случайную с детерминированным трендом величину:
![]() , (14)
, (14)
где координаты ![]() представляют собой значение j-той нагрузки в i-тый момент времени [1]. Пусть имеется множество реализаций Р=[P1, Р2, ..., РN] векторов нагрузки. Задача классификации заключается в том, чтобы на основании данных, содержащихся во множестве Р, подобрать такие классифицирующие признаки, которые позволили бы разбить его на М подмножеств (кластеров) так, чтобы каждая реализация нагрузки на систему (ее образ) Рj,
представляют собой значение j-той нагрузки в i-тый момент времени [1]. Пусть имеется множество реализаций Р=[P1, Р2, ..., РN] векторов нагрузки. Задача классификации заключается в том, чтобы на основании данных, содержащихся во множестве Р, подобрать такие классифицирующие признаки, которые позволили бы разбить его на М подмножеств (кластеров) так, чтобы каждая реализация нагрузки на систему (ее образ) Рj, ![]() принадлежала одному и только одному подмножеству разбиения – кластеру и чтобы объекты, принадлежащие одному кластеру, были «сходными», а объекты, принадлежащие разным кластерам, – разнородными.
принадлежала одному и только одному подмножеству разбиения – кластеру и чтобы объекты, принадлежащие одному кластеру, были «сходными», а объекты, принадлежащие разным кластерам, – разнородными.
Образы реализаций векторов нагрузки в пространстве признаков группируются в множества-классы (кластеры), на которые с помощью данного набора признаков разбивается все множество процесса Р. Чтобы сформировать признаковое пространство для кластеризации чаще всего признаки выбирают, исходя из математической модели процесса. В иных случаях – точечные (значения отдельных координат) или интегральные (значения, получаемые в результате математической обработки координат) характеристики (признаки) процесса.
Наиболее предпочтительным является использование интегральных признаков, полученных в результате разложения вектора Рj по системе ортогональных функций, как обеспечивающих наилучшую кластеризацию. Классифицирующие признаки выбирают так, чтобы получаемое с их использованием разбиение множества Р на кластеры удовлетворяло некоторому критерию оптимальности (целевой функции), определяющей качество классификации.
В ряде случаев можно сформировать некоторые параметры, которые могут входить как компоненты в вектор-признаки. В качестве таких характеристик в работе выбраны:
- экстремум модуля сечения n-мерного ядра Вольтерра (ЯВ):
![]() ;
;
- точка экстремума tmax;
- производная функции в точке t=0
![]() ; (15)
; (15)
· интеграл модуля функции
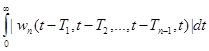 ;
;
- время переходного процесса tnn,
здесь T1,T2,...,Tn-1 ‑ параметры, определяющие диагональное сечение ЯВ n-го порядка (T1≥T2,≥...≥Tn-1). Применение таких эвристических признаков часто позволяет значительно сократить размерность вектора признаков исходного описания. Более универсальный подход при формировании вектора информативных параметров состоит в использовании так называемых моментов ЯВ объекта контроля, которые вычисляются по формуле:
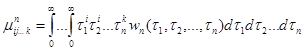 (16)
(16)
здесь i,j,...,k = 0,1,...,∞, i+j+...+k=p – порядок момента.
Представляет также интерес использование метода сжатия диагностической информации с помощью вейвлет-преобразования. Вейвлет-обработка сигналов обеспечивает возможность эффективного сжатия сигналов с малыми потерями информации, тем самым повышая информативность каждого отсчета функции. Прямое непрерывное вейвлет-преобразование функции ![]() здесь задается путем вычисления вейвлет-коэффициентов по формуле:
здесь задается путем вычисления вейвлет-коэффициентов по формуле:
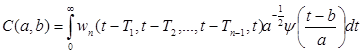 . (17)
. (17)
Интересным представляется и отбора наименьшего числа наиболее информативных признаков с точки зрения классификации как для точечных, так и для интегральных признаков. Данное преобразование есть свертка данных, использование которого резко уменьшает число хранимой классифицирующей информации и объем производимых вычислений.
Решение проблемы свертки базируется на любом из двух подходов. Первый связан с использованием функции энтропии или средней информации при отборе признаков. Второй основан на сравнительной оценке первых и вторых центральных моментов условных плотностей вероятности fi(Pj) (см. подробнее [1]).
3. Синтез исходной системы по критерию минимума среднеквадратической ошибки и метод регуляризации
Здесь рассматривается решение задачи параметрического синтеза нелинейной системы с заданной структурой по критерию минимума среднеквадратической ошибки на модельном примере нелинейного интегро-степенного ряда Вольтерра. Такой подход имеет некоторые преимущества с точки зрения упрощения процедуры расчета [4].
Кроме того, для данной пары разных по топологической структуре локально ограниченных функциональных пространств Е1 и Е2 получена также оптимальная оценка параметра регуляризации.
Предположим, что случайный сигнал x(t) на входе системы представляет собой аддитивную смесь полезного сигнала s(t) и помехи n(t)
x(t)= s(t)+ n(t), (18)
где случайные функции s(t) и n(t) стационарны в узком смысле и стационарно связаны. Требуется, измеряя сигнал x(t), осуществить преобразование полезного сигнала s(t), заданное функцией F[×]:
z(t)= F[s(t)]. (19)
Другими словами, надо определить такое преобразование F[×] сигнала x(t):
y(t)= F[x(t)], (20)
при котором случайные процессы z(t) и y(t) оказались бы близкими по некоторому критерию. В качестве такого критерия использовался минимум среднеквадратического отклонения сигнала у от сигнала z, то есть
M{[y(t)–z(t)]2}=M{(F[x(t)]–F[s(t)])2}=min. (21)
Задача состояла в выделении полезного сигнала s(t) из аддитивной смеси его с помехой n(t) по критерию минимума среднеквадратической ошибки
M{(F[x(t)] –s(t))2}=min. (22)
Задачу об оптимальном преобразовании сигнала (8) целесообразно формулировать как задачу минимизации в ЛОФП, элементы которого F, F, определены на множестве реализаций случайного процесса.
Сначала рассматривалось прямое произведение Z=X´S пространств X, S реализаций случайных процессов x(t) и s(t).
Предполагая известной совместную плотность вероятности
px,s,n,m (x1,…,xn,y1,…,ym,t1,…,tn,τ1,…,τm), (23)
строилась вероятностная мера в пространстве Z.
Показано, что решение основной задачи, выражаемое равенством
(F[x]–F(s), F[x])![]() =0, (24)
=0, (24)
представляет собой полином Вольтерра степени N, имеющий вид:
![]() , (25)
, (25)
Опуская промежуточные выкладки в силу краткости изложения, приведем итоговую формулу (с использованием соображений из [2]):
![]() (26)
(26)
В заключение отметим, что оптимальный синтез в виде интегро-степенного ряда Вольтерра позволяет исследовать НДС с мягкими инерционными нелинейностями и занимает определенный промежуток между методами синтеза линейных систем и методами синтеза нелинейных систем с существенными нелинейностями.
Опишем кратко основную идею метода регуляризации, предлагаемого нами в третьей части работы, для произвольной системы, содержащей Нλ-оператор [2].
Рассмотрим уравнение
Ax=y, (27)
содержащее Нλ-оператор А, где А непрерывен и ограничен; x=x(t), y=y(t) – входной и выходной сигналы, являющиеся элементами ЛОФП Е1 и Е2 соответственно, причем выход y нам задан. Требуется найти из уравнения Ax=y функцию x=x(t). Решение уравнений такого рода, как известно, неустойчиво к изменению данных задачи, если пространства Е1 и Е2 имеют разную топологию. Решение исходного уравнения (27) может даже не существовать в том пространстве, в котором требуется его найти (подробнее см. [1]).
В частности, задача о решении полиномиальных систем интегральных уравнений, определяющих оптимальный нелинейный фильтр, в общем случае является некорректной по Адамару-Тихонову, так как точное решение ![]() неустойчиво к невязкам правой части. Использовался нелинейный регуляризующий функционал вида:
неустойчиво к невязкам правой части. Использовался нелинейный регуляризующий функционал вида:
![]() (28)
(28)
где ![]() (так называемый параметр регуляризации),
(так называемый параметр регуляризации), ![]() и
и ![]() – некоторые функции класса
– некоторые функции класса ![]() ,
, ![]() – образ точного решения
– образ точного решения ![]() .
.
Решая уравнение ![]() (где
(где ![]() – оператор, сопряженный к оператору
– оператор, сопряженный к оператору ![]() ), получим семейство регуляризованных приближенных решений {
), получим семейство регуляризованных приближенных решений {![]() } для исходного уравнения Аx=y в том смысле, что при
} для исходного уравнения Аx=y в том смысле, что при ![]() выполняется предельное соотношение
выполняется предельное соотношение ![]() .
.
Далее в работе показано, что семейство регуляризованных приближенных решений {![]() } стремится к точному решению
} стремится к точному решению ![]() исходного уравнения Аx=y при
исходного уравнения Аx=y при ![]() , иными словами,
, иными словами, ![]() , чем и заканчивается процесс оптимальной фильтрации.
, чем и заканчивается процесс оптимальной фильтрации.
Будем говорить, что оператор А задачи подчиняется условию ![]() , если выполняются неравенства:
, если выполняются неравенства:
![]() и
и 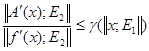 , (29)
, (29)
где вещественнозначные функции ![]() и
и ![]() определены и строго монотонны на
определены и строго монотонны на ![]() + и, если одна из функций возрастает, то другая убывает.
+ и, если одна из функций возрастает, то другая убывает.
Пусть известно, что точка ![]() (
(![]() – нуль пространства Е1), реализует локальный минимум функционала
– нуль пространства Е1), реализует локальный минимум функционала ![]() , а Нλ-оператор подчиняется условию
, а Нλ-оператор подчиняется условию ![]() . Тогда справедлива следующая оценка для параметра
. Тогда справедлива следующая оценка для параметра ![]() , где последний выбирается по «точной невязке»
, где последний выбирается по «точной невязке» ![]() , то есть априорно задана невязка
, то есть априорно задана невязка ![]() [3]:
[3]:
![]() . (30)
. (30)
Рецензенты:
Бахвалов Ю.А., д.т.н., профессор, профессор кафедры «Прикладная математика» Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова», г. Новочеркасск;
Павлов И.В., д.ф.-м.н., профессор, заведующий кафедрой «Высшая математика», Ростовский государственный строительный университет, г. Ростов-на-Дону.



