Для системы очистки зерноуборочного комбайна, предлагается применить рекуперативный привод, предусматривающий установку на верхних концах двуплечих рычагов очистки (в месте крепления шатунов) пружин растяжения-сжатия (пружинных аккумуляторов, с двумя точками неустойчивого равновесия) [4, 5]. Причем на каждом из двух двуплечих рычагов закреплены, по меньшей мере, два пружинных аккумулятора, представляющих собой пружины растяжения-сжатия. Один конец пружинного аккумулятора закреплен при помощи кронштейна на двуплечем рычаге, другой крепится на кронштейне механизма натяжения, позволяющего регулировать натяжение каждого пружинного аккумулятора.
Цель исследования
Цель — совершенствование системы очистки зерноуборочного комбайна путем применения рекуперативного привода решет и транспортной доски для снижения энергоемкости процесса очистки, повышения качественных показателей работы системы.
Одной из важнейших задач, исходя из указанной цели, является исследование кинематики механизма очистки. Для выявления взаимосвязи кинематических параметров механизма очистки зерноуборочного комбайна с его метрическими параметрами необходимо получить аналитические выражения.
Метод исследования
Для кинематического анализа используем аналитический метод векторных контуров [2]. Расчетная схема системы очистки зерноуборочного комбайна рекуперативного привода решет и стрясной доски зерноуборочного комбайна представлена на рисунке 1.
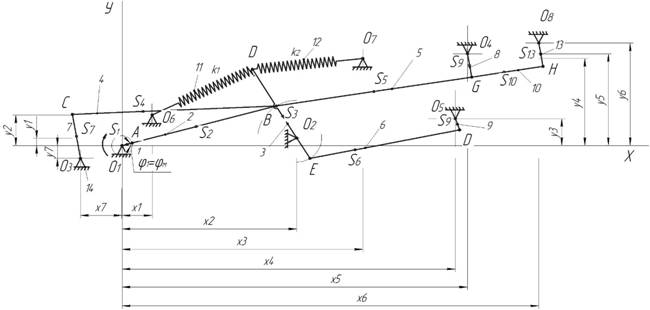
Рис.1.Расчетная схема системы очистки зерноуборочного комбайна:1 – колебательный вал, 2 – шатун, 3 – рычаг, 4 – стрясная доска, 5 – верхнее решето, 6 – нижнее решето, 7, 8, 9, 14 – подвески, 10 – удлинитель верхнего решета, 11,12 – пружинные аккумуляторы, 13 – рычаг, 15 – опора
Разобьём замкнутый четырехугольник на два треугольника О1АО2, АВО2 (рис.2). Для этих контуров составим следующие векторные уравнения:
, (1)
. (2)
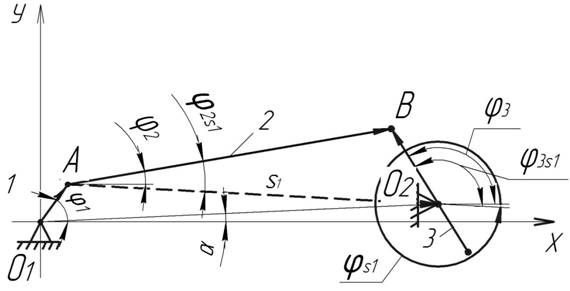
Рис. 2. Схема к определению положений 2-го и 3-го звеньев
где s1 – переменный по модулю вектор, определяющий положение точек А и В механизма;
- длина отрезка О1О2;
- длина шатуна 2; 
- длина отрезка О2В
рычага 3.
Проектируем
векторы уравнения на оси 
. Имеем:
на ось 
,(3)
на ось 
.(4)
Здесь
– угол поворота кривошипа 1;
.
Из уравнений (3) и (4) получаем
Модуль вектора s1из уравнения (4)
Далее, рассматривая треугольник 
получим следующие уравнения:
, (7)
. (8)
Из уравнений (7) и (8) определяем углы наклона векторов l2 и l3к векторуs1обозначенные через φ3s1, φ2s1.
Далее получим выражения для определения углов поворотаφ3, φ2:
Для определения скоростей и ускорений звеньев механизма очистки составляем векторное уравнение замкнутости контура О1АВО2. Имеем
. (13)
Вводя обозначение 
, проецируем уравнение
(2.16) на осиxи yполучим:
, (14)
.(15)
Для определения аналогов угловых скоростей дифференцируем полученные уравнения [3] по обобщенной координате φ1.
Здесь 
передаточные отношения угловых
скоростей ω2 и ω3 к угловой скорости входного
звена ω1. В этом случае уравнения 16, 17 принимают вид
Выполним
поворот осей на угол 
, путем вычитания из уравнения 18:
Далее получаем уравнение
Аналогично
выполним поворот осей на угол 
,
получим
Для определения угловых ускорений дифференцируем уравнения (18), (19) по обобщенной координате φ1:
,
.
Здесь 
, 
- аналоги угловых ускорений
звеньев 2 и 3 соответственно.
Выполняя поворот на угол получим
,
.
Из последних двух уравнений имеем:
Истинные угловые ускорения звеньевε1, ε2, ε3 в данном случае равны:
, 
.
Результаты исследования
Аналогичным образом, определены углы поворота основных звеньев механизма. Выражения для определения углов поворота основных звеньев имеют вид:
где l4, l5,l6,
l7, l8, l9–
длинысоответствующих
звеньев механизма;
- длина плеча О2Е;
– длина плеча О2D;
,
– расстояние между опорами О2
и O6, О2 и О7соответственно.
Здесь
Выражения для определения аналогов угловых скоростей для основных звеньев механизма имеют вид:
Выражения для определения аналогов угловых ускорений для основных звеньев механизма имеют вид:
Истинные ускорения звеньев, в данном случае равны:
,
, 
,
,
.
Длины упругих звеньев 11 и 12при движении механизма определяютсяследующим образом:
Достоверность предложенного подхода подтверждена сравнением полученных результатов решения с результатами решения данной задачи графическим методом.
Выводы
Таким образом, определены аналитические выражения для определения углов поворота, аналогов (передаточных отношений) угловых скоростей и ускорений звеньев, позволяющие определить значения данных параметров в любом положении механизма.
Рецензенты:Пирогов С.П., д.т.н., профессор, профессор кафедры теоретической и прикладной механики ФГБОУ ВПО «Тюменский государственный нефтегазовый университет», г. Тюмень;
Лапшин И.П., д.т.н., профессор, заведующий кафедрой энергообеспечения сельского хозяйства ФГБОУ ВПО «Государственный аграрный университет Северного Зауралья», г. Тюмень.