Обеспеченность предприятия основными фондами в необходимом количестве и ассортименте является одним из важнейших факторов повышения эффективности производства.

На сегодняшний день многие предприятия страдают от износа собственных средств, его уровень достигает 45-65%.

Рассмотрим линейную модель динамики уровня основных средств с равномерным начислением амортизации.

(1)

где - уровень (объем) основных средств в момент времени , - интенсивность ввода реальных валовых инвестиций в основные средства в момент времени , - норма выбытия (износа, амортизации), - неконтролируемое возмущение, - целая часть действительного числа.

Эта модель позволяет решить эту проблему, с помощью грамотного распределения валовых инвестиций и амортизации. Так же в модели учтено запаздывание, которое всегда возникает в реальной жизни.

Позже вводиться импульсное управление, оно помогает нам построить прогноз с учетом различных скачков экономики.

Введем следующие обозначения:

Тогда модель примет вид:

(2)

В качестве показателя функционирования модели рассмотрим интегральный объем основных средств.

(3)

В общем виде краевое условие выглядит следующим образом:

получаем

Пусть , . Тогда будем рассматривать следующую краевую задачу:

(4)

(5)

В соответствии с утверждением (1) подберем функцию такую, что Пусть имеет вид: или

.

Краевую задачу можно свести к интегральному уравнению на основе утверждения (1) из теории краевых задач:

(6)

где

Краевая задача однозначно разрешима и её решение имеет представление:

(7)

где .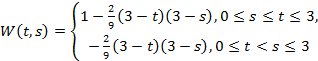

Применим «- подстановку»(7)к уравнению (4) :

где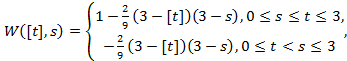

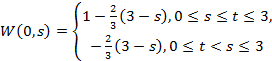
Тогда из (8) получаем:

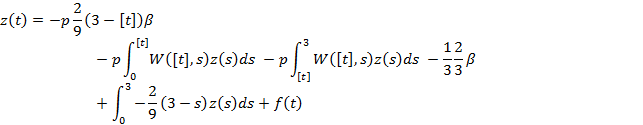
или

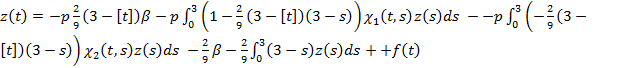(9)

На рисунках (1) – (2) представлен вид функций ,.

: :

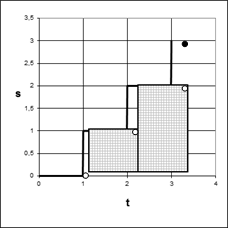
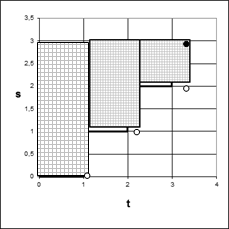Представим каждую из функций , в виде суммы произведений двух функций, одна из которых зависит только от, а другая – только от .

.

Т.к. на промежутке - .

.

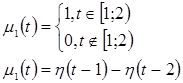
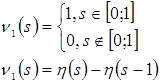
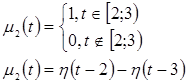
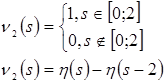
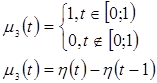
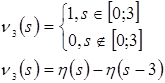
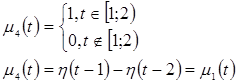
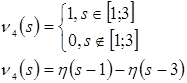
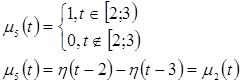
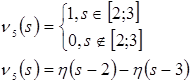
Запишем ядро уравнения (8). Оно будет состоять из двух частей – точной и приближенной.

)

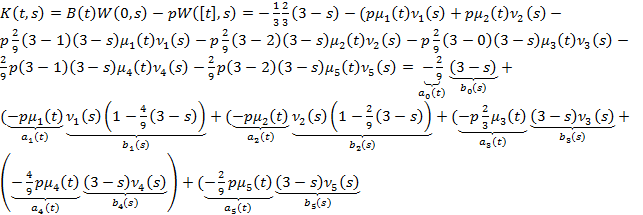Пусть

тогда (10)

Умножим обе части (10) на и проинтегрируем от 0 до 3:

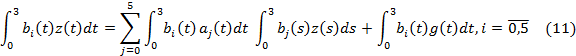
Введем следующие обозначения:

Тогда (11) примет вид: (13)

Если матрица

, , где 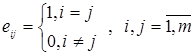(13.1)

имеет обратную матрицу , то уравнение (9) имеет единственное решение :

или

,

где

. (13.2)

Таким образом, краевая задача (1), (3) однозначно разрешима.

Известно, что при естественных предположениях относительно ядра для любого заданного вырожденное ядро можно определить следующим образом:

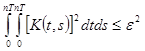. (13.2)

Пусть - матрица , определенная равенством (13.2) и построенная по функциям , , - обратима и . Если выполнено неравенство

,

где

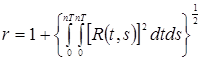, (14)

а функция определена равенством (14), то уравнение (9) с ядром , удовлетворяющим неравенству (16), имеет единственное решение.

Таким образом, доказана теорема:

Теорема 2.

Пусть матрица - обратима и выполнено неравенство , где определено равенством (15). Тогда краевая задача (1),(3) однозначно разрешима, причем ее решение имеет представление

,

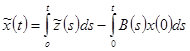с точностью

,

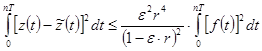и, кроме того,

.

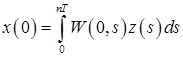Для уравнения введем импульсное управление

(15)

где - дифференцируемая функция, а функция имеет вид

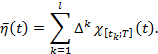
Здесь , – постоянные, - так называемая характеристическая функция отрезка :

Функция является ступенчатой.

.

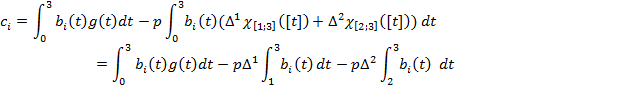
Подставим :

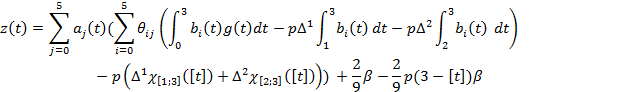
или

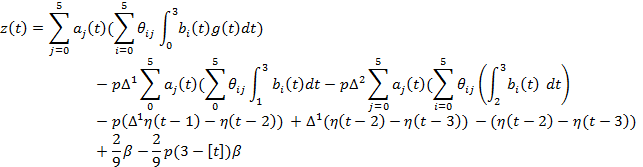
Подставим уравнение (6):

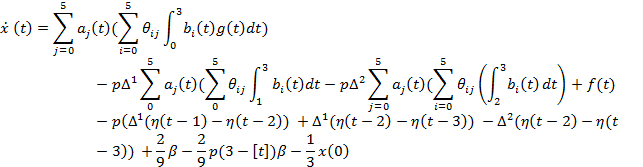
Проинтегрируем обе части уравнения

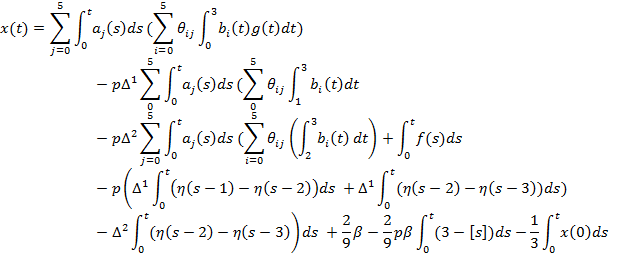
Проинтегрируем обе части равенства от 0 до 3 и находим импульсное управление:

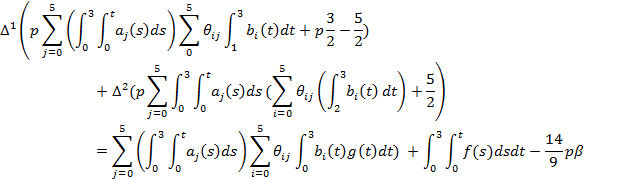
После нахождения импульсного управления в специальных программах, таких как Maple, оно подставляется в уравнение (15). Благодаря этому мы можем решить поставленную задачу.

Рецензенты:

Ёлохова И.В., д.э.н., профессор кафедры экономики и финансов ФГБОУ ВПО "Пермский национальный исследовательский политехнический университет", г. Пермь;

Цаплин А.И. д.т.н., профессор кафедры общей физики ФГБОУ ВПО "Пермский национальный исследовательский политехнический университет", г. Пермь.