Использование алгебраических схем помехоустойчивой защиты является стандартом для большинства цифровых систем хранения и передачи данных. В настоящее время существует большое количество различных помехоустойчивых кодов, методов их комбинирования и модификации, алгоритмов кодирования и декодирования [3-4, 8-10]. Характеристики каналов связи также отличаются многообразием. В связи с этим при проектировании систем связи возникает задача подбора для каждого конкретного канала наиболее эффективных алгебраических схем помехоустойчивого кодирования. В общем случае подбор помехоустойчивого кодека к конкретному каналу связи является сложной многопараметрической оптимизационной задачей. Среди параметров, которые могут интересовать разработчиков систем связи можно выделить: уровень и вид ошибок, действующих в канале; корректирующие свойства кодов по отношению к ошибкам различной структуры и интенсивности; связанная с техническими параметрами средств связи допустимая длина кодового слова; существование эффектов “размножения” ошибок в декодере; требования к объему буферной памяти; быстродействие кодера и декодера; требования к качеству используемого физического канала; степень устойчивости кодека к изменениям характеристик канала и другие. Некоторые из этих характеристик нетрудно оценить априорно, для других же получение оценок является сложной математической задачей (см., например, [3-4]). Следует отметить, что точные математические оценки получаются, как правило, лишь в частных случаях и при обременительных ограничениях.
Эффективность подбора кодеков можно качественно оценить, используя натурные испытания, но как с экономической точки зрения, так и с точки зрения оперативности этот метод оценки не является целесообразным. Наиболее эффективным способом решения задачи приемлемого подбора кодека для канала связи является использование имитационного моделирования. Эту задачу эффективно можно решать в рамках информационной системы (ИС), которая позволит проводить имитационные эксперименты, хранить и анализировать их результаты и принимать решение о целесообразности использования исследуемого кодека в рассматриваемом канале связи.
Цель настоящей работы состоит в разработке структуры ИС исследования эффективности алгебраических схем помехоустойчивой защиты в системах передачи данных. Такая система должна позволять на основе компьютерных имитационных экспериментов оценивать корректирующие способности помехоустойчивых кодеков по отношению к ошибкам различного типа и подбирать оптимальный по заданным параметрам кодек к конкретному каналу связи. В качестве ядра этой ИС будем рассматривать имитационную модель помехоустойчивого цифрового канала передачи данных (ИМ ЦПК).
Имитационная модель цифрового помехоустойчивого канала
Построим ИМ ЦПК согласно классической структуре произвольной имитационной модели, принятой в общей теории имитационных моделей [7] (см. рис. 1). Блок имитации внешних воздействий (БИВВ) формирует реализации случайных или детерминированных процессов, имитирующих воздействия внешней среды на объект. Блок обработки результатов (БОР) предназначен для получения информативных характеристик исследуемого объекта, а необходимая для этого информация поступает из блока математической модели объекта (БMМО). Блок управления имитационной модели (БУИМ) реализует способ исследования имитационной модели, основное назначение этого блока – автоматизация процесса проведения имитационных экспериментов.

Рис. 1. Структурная схема произвольной имитационной модели
Объектом имитационного моделирования является цифровой помехоустойчивый канал (ЦПК) передачи данных. Следовательно, блоком математической модели объекта является блок математической модели ЦПК. На укрупненной структурной схеме (см. рис. 2) БМMО схематично представлен семью блоками: источник сообщений, кодер канала, передатчик, линия связи c шумом, приемник, декодер канала и приемник сообщений.
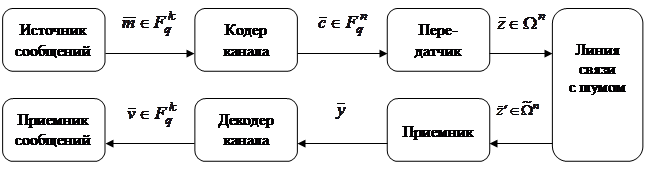
Рис. 2. Схема прохождения данных в моделируемом канале
Источник сообщений выдает информационные векторы ![]() , где
, где ![]() - линейное
- линейное ![]() -мерное пространство, заданное над полем
-мерное пространство, заданное над полем ![]() . С использованием помехоустойчивого
. С использованием помехоустойчивого ![]() -кода С длины
-кода С длины ![]() и размерности
и размерности ![]() , заданного над
, заданного над ![]() , эти векторы обрабатываются в кодере канала. Сформированные кодовые векторы
, эти векторы обрабатываются в кодере канала. Сформированные кодовые векторы ![]() поступают в передатчик, который служит интерфейсом к линии связи и преобразует векторы
поступают в передатчик, который служит интерфейсом к линии связи и преобразует векторы ![]() в векторы
в векторы ![]() . При этом поле
. При этом поле ![]() может как совпадать, так и не совпадать с исходным полем
может как совпадать, так и не совпадать с исходным полем ![]() . Так, например, в работе [4] передатчик получает троичные векторы, а новые формирует над полем комплексных чисел. Сформированные векторы
. Так, например, в работе [4] передатчик получает троичные векторы, а новые формирует над полем комплексных чисел. Сформированные векторы ![]() передатчик на физическом уровне отправляет в линию связи.
передатчик на физическом уровне отправляет в линию связи.
В силу искажений, действующих в линии связи, на выходе из нее формируются векторы ![]() из поля
из поля ![]() , получаемого как расширение поля
, получаемого как расширение поля ![]() . Вектор
. Вектор ![]() поступает на вход приемника, который в зависимости от настроек может выдавать мягкие (
поступает на вход приемника, который в зависимости от настроек может выдавать мягкие (![]() ) или жесткие (
) или жесткие (![]() ) решения о принятом сигнале. Используя принятую в теории связи терминологию, можно говорить, что в случае работы приемника в режиме жестких решений, реализуется цифровой канал, а в случае работы в режиме мягких решений – полунепрерывный канал.
) решения о принятом сигнале. Используя принятую в теории связи терминологию, можно говорить, что в случае работы приемника в режиме жестких решений, реализуется цифровой канал, а в случае работы в режиме мягких решений – полунепрерывный канал.
Вектор ![]() далее поступает в декодер канала. В случае цифрового канала используются декодеры жестких решений, на вход которых поступают значения с выхода демодулятора, преобразующего данные из канала в слова над фиксированным конечным алфавитом. В случае полунепрерывного канала используется декодеры мягких решений (ДМР), особенность которых состоит в том, что в данные из канала связи поступают в декодер без оцифровывания. Обычно использование ДМР дает лучшие результаты по сравнению с декодированием жестких решений, однако обычно декодеры с технологией ДМР обладают большей сложностью [4, 10].
далее поступает в декодер канала. В случае цифрового канала используются декодеры жестких решений, на вход которых поступают значения с выхода демодулятора, преобразующего данные из канала в слова над фиксированным конечным алфавитом. В случае полунепрерывного канала используется декодеры мягких решений (ДМР), особенность которых состоит в том, что в данные из канала связи поступают в декодер без оцифровывания. Обычно использование ДМР дает лучшие результаты по сравнению с декодированием жестких решений, однако обычно декодеры с технологией ДМР обладают большей сложностью [4, 10].
Цель декодера состоит в восстановлении по полученному вектору ![]() информационного вектора
информационного вектора ![]() , посланного ранее источником сообщений. Результат декодирования
, посланного ранее источником сообщений. Результат декодирования ![]() поступает получателю сообщения. В зависимости от уровня повреждения вектора
поступает получателю сообщения. В зависимости от уровня повреждения вектора ![]() в канале связи результат декодирования может совпадать с исходным вектором или отличаться от него. Если
в канале связи результат декодирования может совпадать с исходным вектором или отличаться от него. Если ![]() , то принято говорить о верном декодировании, иначе говорят об ошибке декодирования.
, то принято говорить о верном декодировании, иначе говорят об ошибке декодирования.
Очевидно, что выбираемая в имитационной модели пара кодер-декодер должна быть согласованной. То есть, если кодер осуществляет обработку информации по алгоритму кодирования для некоторого кода с фиксированными параметрами, то декодер должен реализовывать алгоритм декодирования для того же кода и с теми же параметрами. Заметим, что для одного и того же кода могут быть использованы различные кодеры и декодеры. Так, например, рассмотрим известные коды Хемминга. Для этих кодов можно, например, построить кодер, использующий порождающий полином, или кодер, использующий, порождающую матрицу. Декодировать можно, например, алгоритмом, использующим особый вид порождающей матрицы кода, или алгоритмом по минимуму расстояния [8, 10].
Для придания достаточной гибкости имитационной модели необходимо организовать возможность каскадирования кодеков канала и использование перемежителей и деперемежителей. Каскадирование кодеков заключается в последовательном применении нескольких кодеров и декодеров. Например, в системе записи на компакт-дисках используется каскад из двух кодов Рида-Соломона [3]; Консультативным комитетом по системам космических данных для кодирования в телеметрических каналах, рекомендован каскад из сверточного кода и 48 одинаковых (255, 223)-кодов Рида-Соломона.
Цель применения перемежителей и деперемежителей состоит в декорреляции пакетов ошибок, вносимых каналом связи. Перемежение символов является одним из способов улучшения характеристик помехоустойчивости систем передачи в каналах с группированием ошибок [3]. Очевидно, что, так же как пара кодер-декодер, так и пара перемежитель-деперемежитель должны быть согласованными
Задача блока имитации внешних воздействий (см. рис. 1) рассматриваемой ИМ ЦПК заключается в моделировании источника ошибок. Результатом работы этого блока является поток ошибок, который воздействует на передаваемые по линии связи данные. Существует большое количество различных математических моделей источников ошибок [1, 2, 5]. Представляется удобным использовать общую модель источника ошибок канала, которая позволила бы моделировать различные случаи помеховой обстановки, путем изменения ее параметров. Примером такой модели является математическая модель квазипериодических случайных ошибок для двоичных, симметричных и идеально синхронизированных каналов с многобуквенным алфавитом состояний (QPn-модель), позволяющая учитывать нестационарность канала и моделировать принципиально различные случаи помеховой обстановки путем изменения лишь параметров модели [1, 5]. Отметим, что многие известные и широко применяемые на практике модели источников ошибок являются частными случаями QPn-модели.
С помощью блока управления ИМ ЦПК (см. рис. 1) исследователь указывает параметры проводимой серии экспериментов: характеристики последовательности, выдаваемой источником сообщений ИМ ЦПК; кодек или каскад кодеков и перемежителей; параметры источника ошибок; виды статистической обработки результатов эксперимента и необходимость их хранения. БУИМ проверяет корректность введенных параметров проводимых экспериментов. В блоке БУИМ указывается также, какие именно виды статистической обработки применять к результатам имитационных экспериментов в блоке БОР. Следует отметить, что непосредственно в ходе выполнения плана имитационных экспериментов на установки параметров блока БУИМ могут повлиять результаты обработки данных в блоке БОР. Таким образом, возникает задача коррекции заданных параметров.
Одной из задач, решаемых блоком обработки результатов (БОР) в ИМ ЦПК, является вычисление ряда характеристик ошибок, внесенных каналом, и ошибок, оставшихся в сообщении после декодирования. Полагаем целесообразным предоставлять исследователю возможность оценивать основные параметры, рекомендованные к измерению Международным институтом электросвязи ITUT (рекомендации G.821, G.826 и M.2100). К этим параметрам для бинарного канала относятся, в частности, следующие: BIT – число ошибочных битов, EB – число ошибочных блоков, BER – частота битовых ошибок, BLER – частота блоковых ошибок, коэффициент ошибок по блокам и др.
Схема ИС исследования эффективности алгебраических схем помехоустойчивой защиты в системах передачи данных
В настоящее время понятие информационной системы российскими терминологическими ГОСТами не определено. Согласно широко используемому международному справочнику «ATIS Telecom Glossary 2000», выпущенному институтом стандартов США, существует три определения ИС. Самое популярное и наиболее общее из них говорит, что ИС – это автоматизированная система, которая включает людей, машины и/или методы, организованные для сбора, обработки, передачи и распространения данных. Это определение близко к закрепленному ГОСТ 34.003-90 «Комплекс стандартов на автоматизированные системы. Термины и определения» определению автоматизированной системы. А именно: «Автоматизированная система – система, состоящая из персонала и комплекса средств автоматизации его деятельности, реализующая информационную технологию выполнения установленных функций». Далее в работе для определенности будем считать, что информационная система исследования эффективности алгебраических схем помехоустойчивой защиты в системах передачи данных – это система, позволяющая на основе компьютерных имитационных экспериментов оценить корректирующие способности помехоустойчивых алгебраических кодеков по отношению к ошибкам различного типа и подобрать оптимальный по заданным параметрам кодек к конкретному каналу связи. В качестве ядра такой ИС будем рассматривать описанную выше ИМ ЦПК.
Структурная схема ИС исследования эффективности схем помехоустойчивой защиты в системах передачи данных представлена на рис. 3. В состав схемы кроме исследователя входит три компонента: описанная выше ИМ ЦПК (рис. 2); база данных (БД), и блок анализа записей базы данных (БАЗ).
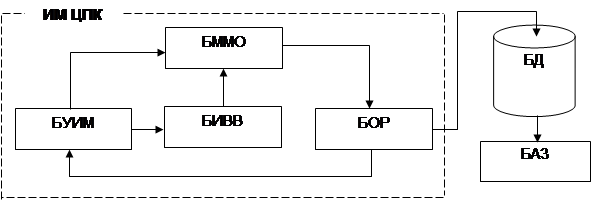
Рис. 3. Структурная схема информационной системы
В базе данных сохраняются все сведения, полно описывающие проведенные эксперименты. К таким сведениям, например, относятся: размер исходного файла (потока информационного сообщения); способ кодирования (использованные кодеки и их параметры, использованные перемежители и их характеристики); характеристика помехи; BIT; EB; BER; BLER; время проведения эксперимента и другие полезные сведения. БД связана с блоком обработки результатов. Сохраняемые в базе данных параметры позволят в дальнейшем анализировать различные аспекты использования помехоустойчивых кодеков. Блок анализа записей базы данных осуществляет составление выборок записей базы по заданным исследователем условиям и построение различных графиков и таблиц.
Заключение
С использованием построенной ИС исследования эффективности алгебраических схем помехоустойчивой защиты в системах передачи данных удобно решать задачу согласования кодека и канала. Для ее решения необходимо проводить имитационные эксперименты, в которых вместо реальных ошибок канала удобно использовать потоки ошибок, сгенерированные согласно одной из математических моделей источника ошибок. Таким образом, рассматриваемая задача согласования фактически решается не для реального канала, а для приближенной модели этого канала. Для подбора согласованной поры кодек-канал необходимо выполнить следующие этапы: подбор исследователем приемлемой модели источника ошибок и её параметров; выбор подходящих кодеков либо по результатам экспериментов из базы данных ИС, либо на основании других теоретических или практических соображений; проведение экспериментов по исследованию корректирующих способностей кодеков с использованием выбранной модели источника ошибок.
Рецензенты:
Звездина М.Ю., д.ф.-м.н., доцент, зав. кафедрой «Радиоэлектроника», Минобрнауки России, ФБГОУ ВПО «Донской государственный технический университет», г. Ростов-на-Дону;
Габриэльян Д.Д., д.т.н., профессор, заместитель начальника научно-технического комплекса «Антенные системы» по науке, Федеральный научно-производственный центр ФГУП «РНИИРС» г. Ростов-на-Дону.



