Информация об ориентации объекта используется в мобильных телефонах и планшетах, в транспортной навигации, в системах управления маневренными объектами (роботами, беспилотными летательными аппаратами и др.). Блок ориентации объекта является также важной частью бесплатформенной инерциальной навигационной системы (БИНС).
В связи с этим весьма актуальной является задача предварительного моделирования бесплатформенной системы ориентации с целью проверки работоспособности ее математической модели и исследования точностных характеристик при работе в различных режимах движения объекта.
Для исследования БСО удобно применить моделирование в программной среде Matlab, где есть возможность построить адекватную математическую модель БСО и получить результаты в реальном масштабе времени в численном и графическом виде. Частично задачи моделирования БСО в Matlab решались в работах [1, 5]. В работе [1] было рассмотрено моделирование алгоритма БСО, использующего кинематические уравнения углового положения объекта уравнения в углах Эйлера-Крылова, с использованием визуальной среды Simulink. В работе [5] рассмотрено моделирование алгоритма БСО, как части БИНС также в рамках Simulink.
Следует отметить, что реализация БСО на основе углов Эйлера-Крылова или направляющих косинусов предполагает решение нелинейных кинематических уравнений при наличии критических точек – так называемых шарнирных замков (Gimbal Lock), что ограничивает их применение в быстродействующих БСО [5, 6]. Большинство авторов БИНС и БСО отдают предпочтение алгоритмам на базе математических моделей с параметрами Родрига-Гамильтона [2, 5, 6]. Кинематические уравнения, составленные в параметрах Родрига-Гамильтона линейны и интегрируемы при любых углах Эйлера-Крылова.
Основной задачей системы ориентации является определение углового положения подвижного объекта в географических координатах – курса (ψ), тангажа (υ) и крена (γ).
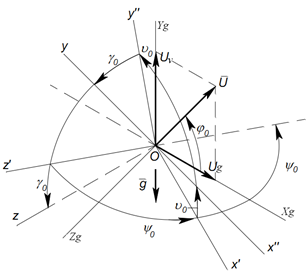
Рис. 1. Углы поворота связанной системы координат X, Y, Z относительно базовой Xg, Yg, Zg
Традиционным является конфигурирование системы ориентации на основе бесплатформенного принципа, при котором роль стабилизированной платформы выполняет виртуальный сопровождающий трехгранник Xg, Yg, Zg, относительно которого определяется положение измерительных осей связанной системы ориентации X, Y, Z в процессе движения объекта (см. рис. 1).
Оси OXgYgZg принадлежат географической системе координат и направлены по сторонам света: на север, по вертикали вверх и на восток (в соответствии с ГОСТ 20058-80), а оси OXYZ связанной с объектом системы координат (приборной) направлены по продольной оси объекта от центра к носу (ось X), вертикально плоскости объекта (ось Y), и перпендикулярно по правому направлению плоскости объекта (ось Z).
Постановка задачи
Задача определения ориентации подвижного объекта заключается в нахождении кватерниона или матрицы перехода из некоторой неподвижной системы координат в систему координат, жестко связанную с объектом.
Измерительные средства, с помощью которых определяют ориентацию подвижного объекта, имеют две группы сенсоров. Первая группа – это датчики направления, определяющие в связанной системе координат некоторое известное в неподвижной системе координат направление (обычно вертикаль места и направление на север). Вторая группа – это датчики угловой скорости (ДУС), измеряющие непосредственно вектор угловой скорости. К первой группе относятся три акселерометра, ко второй – три гироскопа.
Гироскопы служат для определения углового положения измерительных осей относительно базового сопровождающего трехгранника, то есть углов крена, тангажа и курса объекта. Показания акселерометров, как и в платформенных системах, служат для определения вертикали места. Перед началом движения объекта осуществляется выставка БСО, то есть определение начального углового положение измерительных осей (X, Y, Z) относительно осей базового сопровождающего трехгранника (Xg, Yg, Zg).
Гироскопы могут достаточно точно определять угловую скорость подвижного объекта, но их показания плывут со временем. Для коррекции этого дрейфа применяются акселерометры, которые указывают на вертикаль к центру земли.
Датчики угловой скорости выдают сигнал, пропорциональный абсолютной угловой скорости в связанной системе координат. Угловая скорость, измеряемая в связанной системе координат, складывается из вектора переносной угловой скорости земной системы координат, вызванной вращением земли, содержит вектор переносной угловой скорости, связанной с перемещением объекта относительно земли с линейной скоростью и включает вектор угловой скорости связанной системы координат относительно базовой. Для правильного определения углов υ, γ, ψ из показаний ДУСов надо исключить проекции векторов переносной угловой скорости, перечисленные в связанную. Для вычисления переносного движения объекта используется математическая модель угловых скоростей широты и долготы.
Математическая модель бесплатформенной системы ориентации
Алгоритм определения ориентации на основе данных об угловой скорости следующий: сначала задаётся положение подвижного объекта в земной системе координат в начальный момент времени, затем интегрируется кватернионное кинематическое уравнение Пуассона [6]
![]() (1)
(1)
где Λ – кватернион, определяющий переход из системы координат OXgYgZg к системе OXYZ; Ω, Ωg – гиперкомплексные отображения векторов абсолютной угловой скорости связанной и горизонтальной систем координат соответственно.
С учетом медленного ухода нормы кватерниона от единицы при реализации БСО на практике решается кинематическое уравнение с коррекцией нормы кватерниона [6]:
![]() (2)
(2)
где Λ2=λ02+λ12+λ22+λ32 – норма кватерниона; λ0, λ1, λ2, λ3 – параметры Родрига-Гамильтона.
Алгоритм ориентации, основанный на решении уравнения (2), позволяет определить собственный кватернион ориентации между горизонтальной и связанной системами координат при задании начальных условий Λ(0) [5].
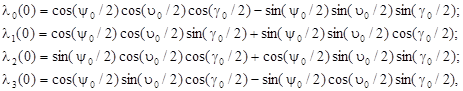 (3)
(3)
где ψ0, υ0, γ0 – начальные значения углов рыскания, тангажа и крена.
Начальные значения углов υ0 и γ0 определяются на основе проекций ускорения свободного падения на оси связанной системы координат:
![]() (4)
(4)
где gX, gY, gZ – проекции ускорения свободного падения на оси связанной системы координат, измеряемые акселерометрами при равномерном движении объекта.
Проекции угловых скоростей от вращения Земли и перемещения объекта в базовой системе координат позволяют также вычислить угол ψ0:
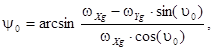 (5)
(5)
где ωXg, ωYg, ωZg – проекции абсолютной угловой скорости географической системы координат на ее оси.
Проекции ωXg, ωYg, ωZg, в свою очередь, определяются следующими известными соотношениями:
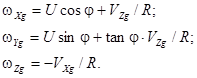 (6)
(6)
где VZg, VXg – составляющие линейной скорости объекта соответственно вдоль оси Zg и Xg географической системы координат; U – угловая скорость вращения Земли; φ – широта местоположения объекта; R – радиус Земли.
Вычисление начальных условий для кинематического уравнения (2) необходимо производить периодически для компенсации довольно значительного дрейфа показаний ДУСов (0,02 – 0,03 град/с). Однако режим компенсации можно применять только в моменты прямолинейного равномерного движения объекта. Такой режим можно определить по показаниям акселерометров, когда ![]() , где ax2, ay2, az2 – составляющие кажущегося ускорения на оси связанной системы координат.
, где ax2, ay2, az2 – составляющие кажущегося ускорения на оси связанной системы координат.
По элементам найденного в результате интегрирования кватерниона (см. уравнение 2) определяются углы ориентации [6]:
 (8)
(8)
Компенсации дрейфа показаний ДУСов осуществляется на основе показаний акселерометров, измеряющих кажущееся ускорение в виде проекций на оси связанной системы координат. Известные алгоритмы выделения ускорения свободного падения из кажущегося ускорения и информация о скорости движения объекта относительно земной системы координат позволяют дополнительно определить все три угла поворота связанной системы координат относительно земной. Это решается путем вычисления дополнительного кватерниона углового вращения объекта с его пересчетом в углы Эйлера. Дополнительный кватернион используется в качестве измерений для фильтра Калмана, который в свою очередь позволяет отфильтровывать имеющиеся измерительные шумы акселерометров и выделить ошибки дрейфа гироскопов.
Моделирование БСО в программной среде Matlab
Моделирование БСО выполняется в программной среде Matlab на основе управляющей программы и ряда программ-функций. При реализации математической модели БСО частично использованы программы из [3] и [4].
В целом алгоритм БСО представлен на рис. 2. Алгоритм БСО имеет блок предстартовой выставки, когда линейные скорости движения объекта отсутствуют, а углы ψ, υ, γ выставлены случайным образом в разрешенных пределах. С целью моделирования работы алгоритма БСО в нем предусмотрена симуляция линейного и углового движения объекта с учетом начальных условий. Симуляция кажущегося ускорения объекта на основе ускорения свободного падения, кариолисова ускорения и собственного ускорения позволяет вычислять линейные скорости объекта по отношению к Земле и его положение в виде широты и долготы земной системы координат.
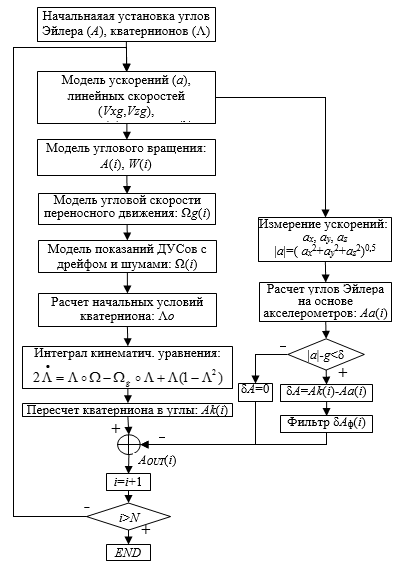
Рис. 2. Блок-схема алгоритма БСО
Угловая скорость вращения объекта (относительная угловая скорость вращения связанной системы координат относительно базовой) в виде проекций на оси связанной системы координат моделируется путем вычисления производных от соответствующих углов поворота. Реальные показания ДУСов содержат, как переносные скорости, зависящие от вращения Земли и от линейного перемещения объекта, так и относительные – от вращения связанной системы координат относительно базовой. Кроме того, они включают дрейф показаний микрогироскопов на уровне 0,02 – 0,03 град/с.
Расчет текущего кватерниона Λ выполняет блок «Интеграл кинематического уравнения». Пересчет кватерниона в текущие значения углов ψ, υ, γ выполняет блок «Пересчет кватерниона в углы Эйлера». Численное интегрирование уравнения Пуассона (2) в данной задаче моделирования реализуется на основе метода Эйлера [2].
Параллельная ветвь алгоритма осуществляет обработку показаний акселерометров, выполняя контроль кажущегося ускорения. При незначительном отклонении кажущегося ускорения относительно ускорения свободного падения (выполнение условия ограничения) производится включение блока коррекции.
Моделирование работы алгоритма производится в рамках N циклов дискретного времени. Программное обеспечение БСО включает:
[a,V,phi,lamb]=navigat(phio,lambo) – модель ускорений, линейных скоростей, углов φ, λ;
[Aa]=acsel_A(V,h,phi(i),t(i)) – блок вычисления сигналов акселерометров;
[A1,phi(i+1),lamb(i+1)]=IMU_angle(Aa,V,phi(i),lamb(i),t(i)) – симуляция модели углов;
[Wg]=Wg_velosity(A1,V,phi,h) – переносная угловая скорость Wg в системе Xg,Yg,Zg;
[Ws]=angle_Wo(A,A1,D,dt,t(i)) – блок формирования сигналов угловой скорости с ДУСов (с учетом относительной и переносной составляющих и дрейфа);
[L]=BCO_kvat(Ws,Wg,dt) – решение уравнения Пуассона (2) (с дрейфом)
[Ak]=kvat(L) – пересчет кватерниона в углы ψ, υ, γ;
[A]=filter(Ak,Aa,dt) – компенсация ошибок дрейфа.
Для примера при моделировании БСО начальное угловое положение объекта задавалось следующим: широта и долгота местности φ0=π/24 рад, λ0= π/13 рад; углы рыскания, тангажа и крена ψ0=π/32 рад, υ0=π/48 рад, γ0=π/32 рад; период дискретности был выбран равным dt=0.01 с, общее время моделирования составило 60 с. Дрейф ДУСов первоначально задавался равным 0,002 град/с (в Matlab это составило: dwx=pi*0.002/180; dwy=pi*0.002/180; dwz=pi*0.002/180).
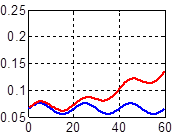
Результаты моделирования БСО при таких исходных данных представлены в виде графиков основных процессов и численных результатов по ошибкам оценивания углов ориентации. На графиках рис. 3 представлены оценки углов ориентации на фоне их реальных значений без компенсации дрейфа гироскопов.
 а)
а)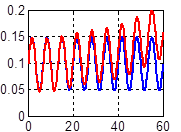 б)
б) 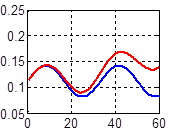 в)
в)
Рис. 3. Счисление углов Эйлера без компенсации дрейфа: а) угла ψ, б) угла υ, в) угла γ (оценки представлены на верхних линиях)
Предельные относительные погрешности оценивания углов без компенсации дрейфа гироскопов (0,002 град/с) за 60 секунд составили следующие значения: dEt=0.442 – угла тангажа; dEg=0.1773 – угла крена; dEp=0.1769 – угла курса. В процентах погрешности оценивания углов в этом случае составляют от 17,7 % до 44,2 %, что для практики оценивания углов в длительном времени является недопустимым. В качестве дополнительного эксперимента были получены также ошибки при дрейфе 0,02 град/с – они составили очень большие значения: dEt=4.5845; dEg=1.5059; dEp=1.4356, т.е. более 400 %.
Решение задачи оценивания углов с компенсацией дрейфа гироскопов при использовании полного алгоритма БСО (см. рис. 2) дает уже достаточно приемлемые результаты. Следует отметить, что алгоритм тестировался при повышенном в 10 раз дрейфе микрогироскопов, т.е. на уровне 0,02 град/с. Численные значения предельных относительных погрешностей в течение 60 секунд в этом случае составили: dEt=0.002; dEg=0.00063; dEp=0.00054, что в процентах не превышает 0,2 %. Погрешности сохраняются на приемлемом уровне и в течение более длительного времени действия алгоритма (не отмечено увеличения погрешностей при оценивании в течение 10 минут). Результаты моделирования БСО с компенсацией дрейфа представлены на графиках рис. 4.
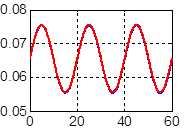
На каждом из рис. 4 (а, б, в) по аналогии с рис. 3 представлено по два графика – один соответствует реальному углу, другой оценке с помощью кватерниона. На рисунках графики оценок практически покрывают графики реальных углов и их идеальные значения не видны.
 а)
а) 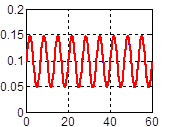 б)
б) 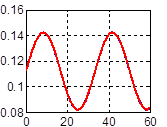 в)
в)
Рис. 4. Счисление углов Эйлера с компенсацией дрейфа: а) угла ψ, б) угла υ, в) угла γ
Выводы
Математическая модель бесплатформенной системы ориентации построена на основе традиционных кинематических уравнений Пуассона с использованием параметров Родрига-Гамильтона.
Моделирование алгоритма БСО проведено с помощью программной среды Matlab. В качестве результатов моделирования приведены графики основных процессов и численные результаты по ошибкам оценивания углов ориентации. Ввиду незначительного расхождения результаты в виде графиков оценок на рис. 4 практически совпадают с реальными углами, что доказывает эффективность компенсации ошибок дрейфа показаний гироскопов.
Новым результатом, полученным в статье, является алгоритм компенсации дрейфа в измерительных данных гироскопов. Таким образом, решена задача компенсации дрейфа показаний микрогироскопов, как основной ошибки БСО. Эффект компенсации дрейфа достигнут с помощью информация с микроакселерометров, измеряющих кажущееся ускорение подвижного объекта. Учет шумов акселерометров и гироскопов в алгоритме БСО осуществляется с помощью фильтра Калмана.
Результаты компьютерного эксперимента подтверждают эффективность алгоритма БСО в системах определения пространственного положения маневренных подвижных объектов в широком диапазоне сигналов и шумов.
Рецензенты:
Вавилов В.Д., д.т.н., профессор, профессор кафедры “Авиационные приборы и устройства”
ФГБОУ ВПО НГТУ, Арзамасский политехнический институт (филиал), г. Арзамас;
Ямпурин Н.П., д.т.н., профессор, профессор кафедры “Конструирование и технология радиоэлектронных средств”, ФГБОУ ВПО НГТУ, Арзамасский политехнический институт (филиал), г. Арзамас.



