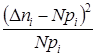Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Среди различных показателей, характеризующих эффективность функционирования электрических сетей, центральное место занимает надежность, связанная с бесперебойностью электроснабжения потребителей. Перерывы в электроснабжении приводят к нарушению технологических процессов на предприятиях, сокращению выпуска и порче продукции, существенно влияют на процессы жизнедеятельности населения.

Установлена система показателей, характеризующих надежность электрических сетей [1]. В качестве основных характеристик обычно рассматриваются: параметр потока отказов и среднее время восстановления. Наличие значений рассматриваемых характеристик позволяет рассчитать другие показатели надежности, такие как коэффициент готовности, коэффициент технического использования, вероятность безотказной работы.

Определение параметра потока отказов и среднего времени восстановления представляет определенные трудности, поскольку такие характеристики специфичны для сетей каждого из поселений и для их установления необходим сбор и обработка статистических данных.

Основные результаты исследования

Существующая практика фиксации аварийных отключений в городских электрических сетях предусматривает ведение в оперативных службах специальных журналов в бумажном или электронном виде. Форма представления информации может быть различна. Проведенный анализ показал, что с целью автоматизации последующей обработки исходных данных, их целесообразно представить в следующем виде (таблица 1):

Таблица 1

Информация об аварийных отключениях

Фрагмент данных, приведенных в этой таблице, взят из диспетчерского журнала Железноводских электрических сетей Ставропольского края, рассматриваемых в качестве объекта исследования в данной статье.

При этом первые три столбца приведенной таблицы позволяют непосредственно получать исходный массив статистической информации, а последующие столбцы анализировать такие характеристики, как причины отключений, отключаемые участки сети,

В качестве примера рассмотрим массив статистической информации об аварийных отключениях в Железноводских городских электрических сетях Ставропольского края за три года с 2011 по 2013 год, содержащих нарушения работоспособности. Установлено, что параметр потока отказов для данных сетей откл/год.

Сложнее решается задача определения среднего времени восстановления. Время ликвидации аварийной ситуации является случайной величиной и для ее анализа необходимо использовать вероятностно-статистический подход.

Математический аппарат обработки статистических данных хорошо известен и сводится к решению двух задач: формированию статистического ряда и оформлению его в виде гистограммы, а также выдвижению гипотезы о законе распределения случайной величины, построению теоретической кривой и проверке сходимости теоретического и статистического распределений [2].

В практике работы городских электрических сетей указанная задача обычно решается вручную. Назрела необходимость автоматизации такого процесса. Рассмотрим последовательность обработки статистических данных и необходимые алгоритмы для выполнения расчетов.

В рамках решения первой задачи, связанной с предварительной обработкой статистических данных, необходимо выполнить следующие процедуры: создать таблицу потока отказов, выполнить группировку исходных данных в вариационный ряд в порядке возрастания (убывания) случайной величины, построить гистограмму. Следует заметить, что при большом числе наблюдений (порядка сотен) вариационный ряд перестает быть удобной формой записи статистического материала. В такой ситуации его необходимо подвергнуть дополнительной обработке. Весь диапазон полученных значений случайной величины следует поделить на интервалы и подсчитать количество членов выборки, приходящихся на каждый интервал. Полученные значения делятся на общее число наблюдений и определяются частоты соответствующие данному разряду. Сумма частот всех разрядов должна быть равна единице. Указанный прием был применен к массиву информации об аварийных отключениях Железноводских городских электрических сетей, в результате получены данные, представленные в таблице 2.

Таблица 2

Значения частоты появления отключений различной длительности

в городских электрических сетях

Полученный статистический ряд необходимо оформить в виде гистограммы, которую построим следующим образом. По оси абсцисс отложим разряды и на каждом из них построим прямоугольник, площадь которого равна частоте данного разряда.

С целью автоматизации процедур обработки исходной статистической информации и построения гистограммы, разработан алгоритм, блок-схема которого представлена на рисунке 1.

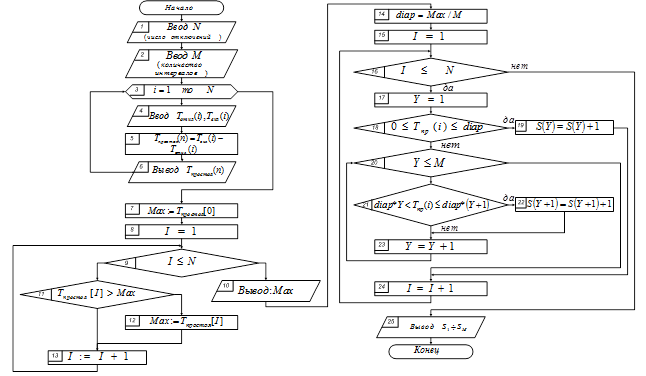
Рисунок 1. Блок-схема алгоритма обработки статистической информации и построения гистограммы

По указанному алгоритму разработано программное обеспечение в среде Visual Basic. Результаты машинной обработки статистических материалов по аварийным отключениям в Железноводских городских электрических сетях представлены на рисунке 2.

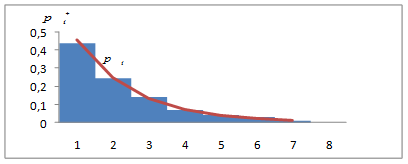
Рисунок 2. Гистограмма длительности отключений в городских электрических сетях

По виду полученной гистограммы можно выдвинуть гипотезу о предполагаемом законе распределения случайной величины. В рассматриваемом случае это будет экспоненциальный закон распределения. Имеющиеся в технической литературе сведения [3, 4] говорят о возможности использования такого закона распределения для электрических сетей в большинстве случаев.

Зная закон распределения случайной величины времени аварийных отключений и определив среднее время восстановления по формуле можно найти значения теоретической кривой . При этом частоты теоретической кривой определяются как приращения функции распределения на -ом участке [5]. Теоретическая кривая, построенная по значениям показана на рисунке 2.

Сравнивая гистограмму с теоретической кривой можно заметить, что между ними имеется расхождение. На практике такое расхождение всегда неизбежно. Следовательно, возникает вопрос о согласованности теоретического и статистического распределений. Такая проверка осуществляется по критериям согласия. Воспользуемся критерием -Пирсона, как наиболее часто применяемым.

Критерий - Пирсона не требует построения самого закона распределения. Достаточно задаться только общим видом функции , а входящие в нее числовые параметры определяются по данным эксперимента. При использовании критерия - Пирсона мера расхождения определяется по формуле

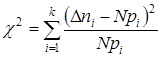(1)

где - число интервалов статистического ряда;

- вероятность попадания случайной величины в -й интервал, вычисленная для теоретического распределения;

- число испытаний.

Для применения критерия - Пирсона необходимо, чтобы и . Рассматриваемый нами исходный массив статистической информации удовлетворяет этим условиям.

Распределение зависит от числа степеней свободы , где - число вычисляемых параметров распределения. Зная величину и по таблицам, приводимым в литературе по математической статистике можно определить вероятность , характеризующую степень расхождения. Если , то обычно считают, что теоретическое распределение не противоречит экспериментальным данным.

Таким образом, проверка сходимости теоретического и статического распределения представляет ряд математических процедур, позволяющих определить величину вероятности .

Нами разработан алгоритм проведения вычислений, блок-схема которого представлена на рисунке 3, а также программное обеспечение в среде Visual Basic, позволяющее проводить необходимые расчеты.

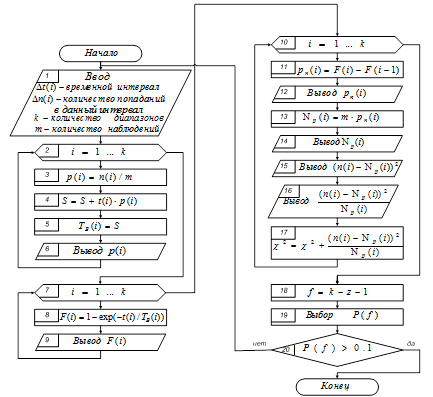
Рисунок 3. Блок-схема алгоритма расчета надежности по статистическим данным

Результаты проверки сходимости теоретического и статистического распределений, показанных на рисунке 2, представлены в таблице 3.

Таблица 3

Результаты проверки сходимости теоретического и статического распределений

Полученная величина =0,98 малой не является и, следовательно, гипотезу о том, что время восстановления аварийных ситуаций в Железноводских городских электрических сетях подчиняется экспоненциальному закону можно считать правдоподобной.

Выводы

Таким образом, в результате проведенных исследований: разработано алгоритмическое и программное обеспечение, позволяющее автоматизировать процесс обработки статистических данных об отключениях в электрических сетях; получены конкретные данные по надежности Железноводских электрических сетей (откл/год, ч).

Рецензенты:

Калмыков И.А., д.т.н., профессор, профессор кафедры информационной безопасности автоматизированных систем института информационных технологий и телекоммуникаций Федерального государственного автономного образовательного учреждения высшего профессионального образования «Северо-Кавказский федеральный университет», г. Ставрополь.

Федоренко В.В., д.т.н., профессор, профессор кафедры прикладной математики и математического моделирования института математики и естественных наук Федерального государственного автономного образовательного учреждения высшего профессионального образования «Северо-Кавказский федеральный университет», г. Ставрополь.