Прогнозирование эффективности маркетинговых кампаний является сложной и актуальной задачей. Существенный объем работ в этом направлении прилагается для понимания того, за какие сроки идея кампании устаревает и перестает приносить какой-либо результат. Это особенно актуально для вирусного маркетинга. [1]. Ставка на вирусное распространение является экономически эффективной только в случае, если обычная рекламная кампания, равная по продолжительности периоду присутствия вирусного момента, оказывается существенно дороже вложений в вирусный контент. Вместе с тем на сегодняшний день даже в сфере интернет-маркетинга, наиболее точно прогнозируемого направления продвижения товаров и услуг, не существует каких-либо инструментов для решения этой задачи.
В данной работе предложен математический аппарат для оценки изменения эффективности вирусного маркетинга (вследствие устаревания контента) и принятия управленческого решения о целесообразности ее использования. Он основан на популярной модели математической биологии – логистической модели [2]. Эта зависимость широко известна как модель Ферхюльста для расчета изменения численности популяции при ограниченных ресурсах. В рамках использования модели для решения задачи оценки темпов роста результатов вирусных маркетинговых кампаний будет предложено нахождение неизвестных коэффициентов модели, отвечающих описываемым процессам [3].
Структура работы выстроена следующим образом: сначала приводятся краткие сведения о принципах логистической модели, затем этот математический аппарат адаптируется для решения поставленной задачи. После этого дается практический пример: расчет темпов роста результатов вирусной маркетинговой кампании на примере реального предприятия.
1. Общие сведения о модели Ферхюльста
Изначально рост популяции объяснялся экспоненциальным законом, впоследствии получившем название модель неограниченного роста популяции. Такой закон имеет смысл лишь на небольшом временном промежутке, так как в естественной среде рост обязательно ограничивается рядом факторов: смертностью, исчерпаемостью ресурсов, природными условиями и т.д. Модели, предлагаемые в дальнейшем, описывали рост популяции, переходящий в фазу стабилизации, что гораздо лучше отвечает реальным условиям. Стабилизация происходит под влиянием указанных выше факторов, совокупность которых получила название «сопротивление среды» [4].
Математическое описание данной идеи было дано Ферхюльстом в виде логистического закона.
Пусть 
– число организмов, 
– время, 
– реальная скорость размножения, 
– потенциальная скорость размножения (удельный прирост популяции в условиях отсутствия сопротивления среды), тогда 
.
Решив полученное уравнение, получим классический закон изменения численности популяции в условиях неограниченного роста: 
Для описания процесса в условиях присутствия сопротивления среды была предложена следующая поправка:
Пусть 
– максимальный размер популяции в условиях ограниченности ресурсов и факторов среды, 
– относительные возможности роста (процентная оценка потенциального роста популяции), тогда справедливо 
– логистическая кривая Ферхюльста – Перля.
Можно вычислить интересные для исследователя параметры: 
– сопротивление среды,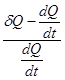 
– интенсивность борьбы за существование.
Далее убедимся, что принципы логистической модели отлично применимы к прогнозированию эффективности вирусного маркетинга.
2. Адаптация логистической модели роста популяции к задаче оценки темпов изменения эффективности вирусного маркетинга
Эффективность маркетинга является сложным комплексным понятием, влияние на изменения которого оказывает целый ряд факторов [5]. В данной работе сфокусируемся на такой составляющей этого понятия, как эффективность маркетингового контента.
Определим понятие эффективности контента.
В рамках этой работы удобно вкладывать в этот термин удельный смысл. Поэтому под изменением эффективности контента будем понимать изменение максимального числа человек в единицу времени, совершивших целевое для маркетинговой капании действие.
Логистическая модель хорошо подходит для описания этого процесса в случае вирусного маркетинга, так как:
1) Аудитория любой маркетинговой капании всегда ограничена.
2) На старте рекламной кампании аудитория не охвачена, а значит, имеется потенциал роста.
3) В общем случае за аудиторию происходит конкурентная борьба, не все люди из аудитории оказываются способны совершить максимальное число целевых действий – имеются естественные ограничения на потенциал роста.
4) В процессе вирусного распространения маркетингового контента каждый новый участник способен сгенерировать некоторое количество человек, совершивших целевое действие.
5) Пункты 1 – 4 характерны абсолютно для всех вирусных маркетинговых кампаний.
В доказательство, кроме теоретических рассуждений, приведем также графики эффективности реальных рекламных кампаний.
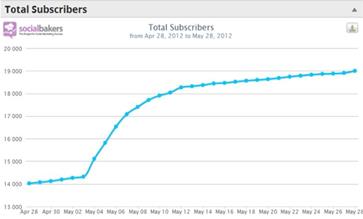
На рисунке 1 показан результат вирусной маркетинговой кампании сайта Socialbaker (количество человек, зарегистрировавшихся на сайте). Сходство с традиционной логистической кривой очевидно:
Рисунок 1
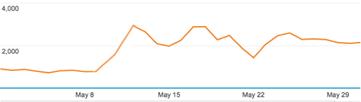
На рисунке 2 показаны результаты маркетинга игры Anime Pirates. Здесь наблюдается форсированный рост до максимального результата с изначально небольшим потенциалом:
Рисунок 2
Таким образом, будем считать, что правомерность применения логистической модели роста популяции для расчета изменения темпов роста результатов маркетинговой кампании обоснована.
Тогда переменные модели приобретут следующий смысл: – результат маркетинговой компании: количество человек, совершивших целевое действие, 
– время, – скорость роста результатов кампании, – потенциальная скорость роста кампании, – максимальный размер охваченной целевой аудитории.
Оставшиеся переменные будут нести традиционный для экономической трактовки логистической модели смысл: – свободные возможности роста, – конкурентное сопротивление и погрешности выбора аудитории, 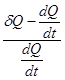– интенсивность конкурентной борьбы.
Особого внимания заслуживает выражение потенциальной скорости роста кампании . Говоря о маркетинговой кампании, мы имеем дело с системой, потенциал самовоспроизводства которой крайне мал. Смысл любой маркетинговой кампании состоит в выполнении функции воспроизводства. Исключением является вирусный маркетинг, совершенно особенный вид маркетинга, смысл которого состоит в генерации «толчка» для самовоспроизводства результатов. Как правило, стоимость такой однократной генерации, имеющей взрывной пролонгированный эффект, оказывается существенно ниже совокупной стоимости традиционной рекламной кампании, ориентированный на тот же результат.
Задачей подготовки к построению логистической модели, таким образом, будет являться определение величины . Здесь можно выделить два возможных подхода:
1) Прогнозирование на основе статистических данных и экспертных оценок. Плюсами подхода являются возможность определить эффективность рекламной кампании до ее начала и возможность отказаться от использования вирусного маркетинга. Минусами – низкая точность таких прогнозов.
2) Использование данных, полученных в первую единицу времени наблюдения, с наложением на них некоторых погрешностей. Плюсы подхода – очень высокая точность прогнозирования. Минусы – невозможность изменить решение об использовании вирусного маркетинга.
Решив уравнение Ферхюльста – Перля , получим: 
, где 
.
3. Расчет темпов роста результатов вирусной маркетинговой кампании на примере реального предприятия
В качестве практического примера будем использовать вирусную интернет-кампанию f2p онлайн-игры Anime Pirates, реализованную кампанией-паблишером игры.
В качестве вирусного контента была подготовлена серия баннеров и текстов к ним. Стоимость базового контента можно условно принять равной 0, так как их создание было реализовано силами штатных работников предприятия.
Поэтому за стоимость вирусной рекламы примем вложения в привлечение самых первых пользователей, говоря в терминах модели роста популяции – вложения в составление основы популяции, производства ее первых представителей. Для распространения вирусного контента была выбрана социальная сеть facebook. Механизмы, предусмотренные в ней для онлайн-маркетинга, позволяют выстроить вирусную рекламную кампанию: существует возможность маскировки рекламы под контент.
С помощью средств этой социальной сети был определен и максимальный размер аудитории – после таргетирования и анализа facebook определил потенциальный размер аудитории как 14 000 000 человек. Исторические данные по конверсии игры были следующими: уровень показов 
– заходы на сайт 
– 5 %; заходы на сайт – регистрации 
– 20 %. Таким образом, величину максимального охвата аудитории можно вычислить как 
. Тогда в данном примере 
. На момент начала маркетинговой кампании в игре было 4543 регистрации. Исходя из оптимистичного прогноза, было сделано предположение, что все эти 4543 человека являются частью . Это означает, что свободные возможности роста составляют 96 %. В данном случае определялась по фактическим значениям первого дня вирусной кампании и составила 6 %. На практике это означало, что примерно 3 % от привлеченных платно первых совершивших целевое действие пользователей (зарегистрировавшихся) принесли хотя бы еще одну регистрацию. Тогда логистическая кривая описывается уравнением 
, где 
.
Так как построение логистической кривой в данном случае имеет чисто научный характер и потому проводилось уже после завершения маркетинговой кампании, есть возможность сравнить теоретические данные, полученные с использованием модели роста популяции, и реальную практическую эффективность маркетинговой кампании.
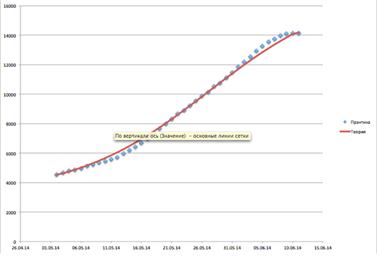
Рисунок 4
Очевидно, что логистическая кривая очень хорошо отвечает реальным данным.
Судя по внешнему виду логистической кривой, после 5 июня 2014 года контент начинает устаревать, а после 10 июня 2014 – вообще перестает давать видимый эффект.
Определим теперь, какими были бы результаты традиционной рекламной кампании. Стоимость вирусной рекламной кампании составила $ 400 – именно столько было потрачено на привлечение базовой аудитории – людей, ставших основой «популяции». По опыту прошлых рекламных кампаний известно, что средняя стоимость регистрации при стандартной маркетинговой кампании на facebook для этой игры составляла $0,18. Это означает, что за $ 400 можно было бы привлечь примерно 2222 человек. Это существенно меньше, чем при использовании вирусного контента.
В работе было предложено применение логистической модели роста популяции для оценки темпов изменения эффективности вирусной маркетинговой кампании. Было показано, что такое применение правомерно и эффективно, а, кроме того, позволяет решить управленческие задачи: понять, когда контент для вирусного маркетинга устареет и более не будет способен приносить существенный результат; определить, что будет эффективнее – вирусный маркетинг (в общем случае с очень дорогим контентом) или традиционный маркетинг (с более дешевым контентом, но зато с оплатой за распространение).
Рецензенты:
Роговой А.А., д.ф.-м.н., профессор, научный сотрудник Института механики сплошных сред, г. Пермь;
Первадчук В.П., д.т.н., профессор Пермского национального исследовательского политехнического университета, г. Пермь.