Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Происходящие в атмосфере пространственно-временные изменения гидрометеорологических величин определяют сложные изменения показателя преломления атмосферы (атмосферная рефракция). Различают случаи, когда в атмосфере имеет место отрицательная рефракция, рефракция отсутствует или же атмосферная рефракция положительна [4]. В качестве основного критерия, используемого при классификации атмосферной рефракции, применяется вертикальный градиент показателя преломления (dN/dh, 1/м) [4].

Наибольшие изменения показатель преломления атмосферы претерпевает по вертикали в нижнем слое атмосферы, что обусловлено большими изменениями в этом слое температуры и влажности [1-5, 7].

В практической деятельности при проведении соответствующих расчетов используются сведения об изменениях показателя преломления атмосферы только по высоте. Горизонтальные же изменения показателя преломления атмосферы в расчетах не учитываются, что является не совсем корректным.

Цель работы - построение модели, отражающей особенности пространственного изменения преломляющих свойств атмосферы на основе использования имеющихся случайных данных о гидрометеорологических величинах.

Материалы исследований. Известно, что градиент некоторой скалярной величины f (grad f) есть вектор, совпадающий с нормалью N к эквискалярной поверхности. По модулю он равен производной от f по N, но с обратным знаком [6]:

(1)

Используемые в практической деятельности сведения об изменении градиента показателя преломления в основном касаются его вертикальной составляющей, поскольку показатель преломления претерпевает значительные изменения по высоте. Это учитывается в различных сферах деятельности, где имеет место рассмотрение вопросов, связанных с атмосферной рефракцией [3].

Достаточно подробно влияние вертикальной составляющей градиента показателя преломления изложено в работе [3] (в условиях представления атмосферы в виде плоско-слоистой среды) и в работе [7] (в условиях, когда имеет место сферическое строение атмосферы).

В [1] была предложена методика расчета отклонений траектории оптического сигнала от прямолинейной, основанная на учете горизонтальной составляющей градиента показателя преломления атмосферы. Полученные в [1, 2] математические выражения позволяют провести расчеты возможных ошибок при определении положения объектов в пространстве, а также вычислить величину угла рефракции. В этих выражениях используется информация о фактическом состоянии гидрометеорологических параметров атмосферы.

Однако рассмотренные в [1, 2] вопросы не в полной мере отражают происходящие в атмосфере процессы.

По определению градиент скалярного поля

(2)

где n=n(x, y, z) – скалярная функция, определяющая поле распределения показателя преломления атмосферы.

Для удобства обозначим

Выражение (2) перепишем иначе:

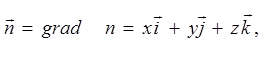(3)

где x, y, z – проекции вектора на соответствующие оси координат. Для данной точки пространства эта величина определяется однозначно.

В работах [3, 7] рассматриваются случаи, когда справедливо следующее соотношение:

(4)

т.е. изменением значений показателя преломления атмосферы n по направлениям Ох и Оу пренебрегают.

В работе [1] учитываются изменения показателя преломления атмосферы в горизонтальном направлении, т.е. по осям Ох и Оу. Тогда:

(5)

Очевидно, что при решении различного рода задач следует учитывать составляющие показателя преломления по всем трем осям декартовых координат.

Для практических расчетов далее предлагается использовать следующую ориентацию: ось абсцисс Ох направить на юг, ось ординат Оу - на восток, а ось аппликат Оz - вверх.

Поместим начало произвольного вектора в начало системы декартовых координат в точку О с - ортонормированным базисом. (на рис. 1).

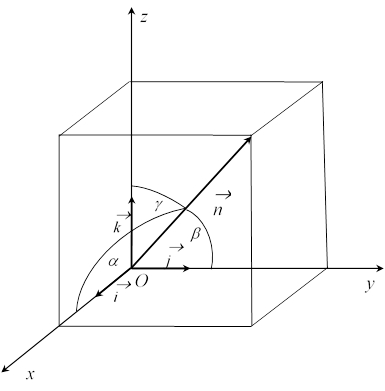Рис. 1.

Разложив вектор по базису, получим:

(6)

где nx, ny, nz – соответствующие проекции вектора на оси координат.

Модуль вектора может быть определен из выражения:

(7)

Из рис. 1 имеем:

(8)

Тогда направляющие косинусы вектора :

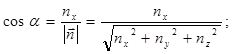
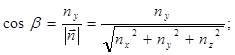(9)

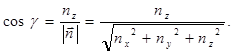
Авторами было проведено восстановление в декартовой системе координат положения градиента показателя преломления по данным температурно-ветрового зондирования атмосферы, проведенного по методике, представленной в [1]. При восстановлении значений показателя преломления атмосферы было использовано известное соотношение [1-3, 5]:

(10)

где р - атмосферное давление (мб);

е – парциальное давление водяного пара (г/м3);

T - температура воздуха (К).

В качестве исходных данных было использовано фактическое состояние атмосферы 23 декабря 2012 года по материалам, представленным на информационном ресурсе http://www.wetter3.de/ в разделе Vertikalschnitte (GFS).

Сведения о величине горизонтальной и вертикальной составляющих градиента показателя преломления атмосферы, выраженных в N-единицах, представлены в таблицах 1 и 2 соответственно.

Таблица 1

Данные о распределении значений горизонтальной составляющей градиента показателя преломления атмосферы (N-ед/100км) вдоль 50° северной широты

Таблица 2

Данные о распределении значений вертикальной составляющей градиента показателя преломления атмосферы (N-ед/100м) вдоль 50° северной широты

Восстановим на примере точки с координатами 15°з.д. и 50°с.ш. модуль градиента показателя преломения атмосферы у земной поверхности и по высотам, а затем рассчитаем значения направляющих косинусов. В качестве исходных данных будем использовать данные, представленные в таблицах 1, 2.

Применяя декартову систему координат (рис. 1), несложно получить по формуле (7) значение модуля градиента показателя преломления атмосферы:

Подставляя в (9) полученное значение, рассчитаем величину соответствующих направляющих косинусов. Получим: cosa=0,00012, cosb=0,00013, cosg=0,99919.

Аналогичным образом были рассчитаны модули градиента показателя преломления у земной поверхности и по высотам в узлах сетки, определяемых на пересечении меридианов через каждые 5° (15°з.д. – 30°в.д.) с параллелью 50°с.ш. Результаты расчетов представлены в таблице 3.

Таблица 3

Значения модуля градиента показателя преломления атмосферы и направляющих косинусов за 23.12.2012 года в слое 0-5000 м.

В результате проведенных расчетов установлено, что максимальные изменения градиента показателя преломления атмосферы наблюдаются по вертикали. Однако имеют место и горизонтальные изменения, но их абсолютные значения на один-два порядка меньше значений вертикальных составляющих.

Установлено, что абсолютные значения градиента показателя преломления незначительно отличаются от значений его вертикальной составляющей. Величина таких отличий находится в пределах от 0 до 0,1 относительно значений вертикальной составляющей. При этом отклонения градиента показателя преломления относительно оси аппликат составляют 1° - 2° (см. значения cosg, таблица 3). Отклонения же градиента по осям абсцисс и ординат находятся в пределах 88° - 89° (см. значения cosa и cosb, таблица 3). Эти отклонения градиента от соответствующих осей координат позволяют говорить о неравномерном характере распределения показателя преломления относительно земной поверхности.

Заключение. Полученные в результате расчетов абсолютные значения градиентов показателя преломления атмосферы и отклонения составляющих градиента показателя преломления по осям декартовой системы координат имеют место, как у земной поверхности, так и по высоте. При рассмотрении вопросов, связанных с влиянием преломляющих свойств атмосферы необходимо учитывать фактические значения параметров атмосферы и их изменения по осям координат. Последнее позволит установить распределение поля показателя преломления в выбранной системе координат по всем осям.

Рецензенты:

Душин А.В., д.т.н., доцент, начальник кафедры управления и информационно-технического обеспечения, ФКОУ ВПО «Воронежский институт ФСИН России», г. Воронеж;

Сумин В.И., д.т.н., профессор, профессор кафедры управления и информационно-технического обеспечения, ФКОУ ВПО «Воронежский институт ФСИН России», г. Воронеж.