В настоящее время магнитоэлектрическое (MЭ) взаимодействия в планарных магнитострикционно-пьезоэлектрических структурах интенсивно изучается вследствие перспективприменения таких структурдля создания устройств функциональной электроники, таких как датчики магнитного поля, преобразователи и накопители электрической энергии [1]. MЭ взаимодействиепроявляется в виде индуцирования электрического напряжения Uв структуре при воздействии внешнего переменного магнитного поляH и возникает благодаря сочетанию магнитострикции в магнитной компоненте и пьезоэлектрического эффекта в пьезоэлектрическойкомпонентеблагодаря механическомуконтакту между слоями. МЭ взаимодействие характеризуется ME коэффициентом по напряжениюαЕ = U/(t H), где t - толщина пьезоэлектрического слоя. Величина индуцируемого напряжения увеличеиваетсяна один-два порядка, когдачастота переменного магнитного поля f совпадает с частотой электромеханического резонанса(ЭМР)структурыв результате резонансного увеличения механических напряжений в пьезоэлектрическом слое [2]. ЭМР возможенвследствие возбуждения в структуреизгибных или планарных колебаний. Использование изгибных колебаний позволяет снизить резонансную частоту на порядок или уменьшить размеры образцапри фиксированном значении частоты.
Для двухслойных структур состава Терфенол – цирконат-титанат свинца ( ЦТС ) был получен МЭ коэффициент по напряжению 14,6 В/(cm∙Э)на частоте изгибных колебаний 12,5 кГц [ 3 ]. Для слоистых структур состава никель-ЦТСи GaFe-ЦТС - были измерены МЭкоэффициенты соответственно 1 В/(cm∙Э) в диапазоне частот 3-7 кГц [ 4 ] и 8,7В/(cm∙Э) на частоте 33,4 кГц [5]. Однако, для образцов с одним пьезоэлектрическим слоем индуцируемое напряжение не достигает своего максимально возможного значения в связи с изменением знака механических напряжений по толщине этого слоя - от сжимающих напряженийдо растягивающих [6].
Для увеличения индуцируемого напряжения может быть использована асимметричная биморфная структура, состоящую из двух слоев ЦТС, которые поляризованы в противоположных направлениях и размещены между двумя магнитными слоями[7, 8]. Для структуры, содержащей два слоя терфенола, был получен МЭ коэффициент по напряжению, значение которого превышает 72В/(cm∙Э) начастоте изгибных колебаний 34 кГц [7]. Следует отметить, что для возбуждения изгибных колебаний в такой структуре необходимо обеспечить противоположные направления намагниченности в магнитных слоях, что сложно реализовать. Целью данной работы является теоретическое моделирование МЭ эффекта в слоистой магнитострикционно-пьезоэлектрической структуре на основе биморфного пьезоэлектрического преобразователя.
1 Моделирование магнитоэлектрического эффекта
Рассмотрим слоистую структуру, состоящую из магнитного аморфного сплава метглас и двух слоев ЦТС с противоположными направлениями поляризации. На рис. 1 представлен образец описанной структуры. Кроме структуры, приведенной на рис. 1 в данной статье рассматривается структура состава:два слоя ЦТС и два слоя метгласа с различными по величине пьезомагнитными коэффициентами.Длина образца выбирается значительно больше остальных геометрических размеров, поэтому рассматривается только одна составляющая тензора механических напряжений и деформаций. Для достижения пьезомагнитного эффекта и линеаризации МЭ свойств слоистой структуры, к материалу прикладывается подмагничивающее поле H0. В этом случае в интервале магнитных полей, малых по сравнению с подмагничивающим полем, магнитострикция проявляется в виде пьезомагнитного эффекта, а МЭ эффект будет близок к линейному.
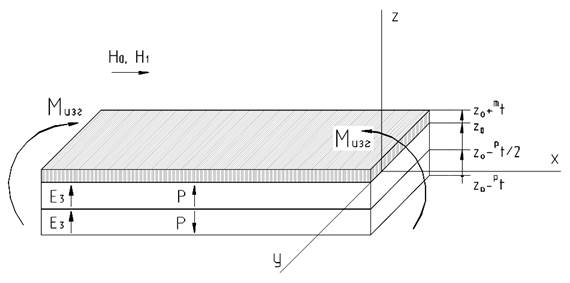
Рис. 1. (а) Слоистая структура состава метглас - цирконат-титанат свинца (ЦТС). Образец длиной L расположен в плоскости XOY, ось z направлена вдоль толщины образца. Подмагничивающее поле H0 и переменное магнитное поле H направлены вдоль оси x. Вектор поляризации пьезоэлектрических слоеви переменное электрическое поле E3направленыперпендикулярно плоскости образца. Ненулевой изгибающий момент Мизг вызывает изгиб образца.
Для построения теоретической модели МЭ эффектаиспользуются уравнения упругости и материальные уравнения для пьезоэлектрического и магнитострикционного слоев:
pSi = psijpTj + pdkipEk;
pDk = pdkipTi + pεknpEn;
mSi = msijmTj + mqkimHk; (1)
mBk = mqkimTi + mμknmHn;
где Si иTjкомпоненты тензоров деформации и механического напряжения, Ekи Dk- компоненты векторов электрического поля и электрического смещения, Hk и Bk – компоненты векторов магнитного поля и магнитной индукции,sij, - податливость; qki иdki- пьезомагнитный и пьезоэлектрический коэффициенты, εkn –диэлектрическая проницаемость и μkn –магнитная проницаемость. Верхние индексы p, m соответствуют пьезоэлектрической и пьезомагнитной фазам, соответственно. Предполагается, что симметрия пьезоэлектрической фазы есть ¥m, а пьезомагнитная фаза обладает кубической симметрией.
МЭ коэффициент по напряжению определяется в результате решения уравнений магнитостатики и эластодинамики в ферромагнетике и уравнений электростатики и эластодинамикив ЦТС с учетом граничных условий. В асимметричных МЭ структурах с переменным составом возникают изгибные деформации, что связано с возникновением в поперечных сечениях образца изгибающих моментов. Теория изгиба основана на гипотезе Бернулли, согласно которой поперечные сечения являются плоскими и перпендикулярными к оси недеформированной балки, причем эти сечения остаются плоскими и перпендикулярными к изогнутой оси после ее деформации. Помимо гипотезы плоских сечений принимаетсядопущение о том, что продольные слои балки при ее изгибе не надавливают друг на друга. Таким образом, деформация сдвига слоев относительно друг друга не учитывается. Единственным напряжением, рассматриваемым в этой теории, является осевое напряжение [9]. Размеры сечения образца предполагаются малыми по сравнению с радиусом кривизны оси балки.
Осевые деформации в слоях магнитострикционно-пьезоэлектрической структуры переменного состава можно рассматривать как сумму продольных деформаций и деформаций за счет изгиба.
S1 (x, z) = du0/dx – z·d2w/dx2, (2)
где u0 – смещение вдоль оси x, w – прогиб структуры (смещение вдоль оси z).
Рассмотрим деформацию образца в процессе изгиба (рис. 2).Выделим элемент структуры длиной dx. В результате изгиба поперечные сечения балки повернутся, образовав угол dθ. Верхние слои испытывают сжатие, а нижние - растяжение. Поверхность, разделяющая сжатую зону от растянутой естьсрединная поверхность. Линия ОО1, принадлежащая срединной поверхности, сохранит свое первоначальную длину dx. Радиус кривизны срединной поверхности обозначим через R.
Рассмотрим деформации слоя, отстоящего на расстоянии zi от срединной поверхностии растянутого напряжениями Tj (рис. 2). Первоначальная длина этого волокна равна dx = Rdθ. После деформацииего длина по дуге dx стала (R+z)dθ. Абсолютное удлинение рассматриваемого волокна ΔL = (R+z)dθ – Rdθ = zdθ. Относительное удлинение по оси х (или деформация нейтральной оси) запишется следующим образом
ubend (х, z)= zdθ/Rdθ = zi/R,
т. е. удлинения волокон пропорциональны их расстояниям до срединной поверхности.
Таким образом, деформацию, возникающую за счет изгиба, можно представить как линейную функцию от вертикальной координаты zi, а продольные деформации представить как относительное удлинение срединной плоскостивдоль оси х. (рис. 2) [35]:
mS1 =mS10 +zm/R;
pS1 =pS10 +zp/R (3)
где тS10 и рS10 – деформации нейтральной оси вдоль оси x при zi =0, R– радиус кривизны нейтральной оси структуры; zi – расстояние от i-го слоя структуры до срединной плоскости.
Запишем граничные условия для образца, в соответствии с которыми на границе раздела магнитострикционной и пьезоэлектрической фаз наблюдается равенство компонент деформаций:
pS1 =mS1, (4)
Очевидно, для деформаций нейтральной осисправедливо следующее выражение:
mS10 - pS10 = hm/R1,
где hm – средняя толщина слоев магнитострикционной и пьезоэлектрической фаз.
|
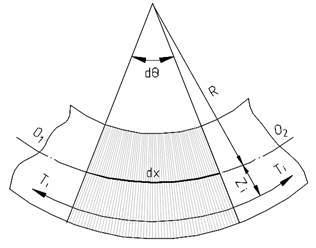
Рис. 2. Деформация структуры при изгибе
Данная модель ограничивается ориентацией полей (рис.1), когда подмагничивающее поле H0 и переменное магнитное поле p параллельны друг другу и лежат в плоскости образца.Предполагается, что слой ЦТС поляризован вдоль оси z и переменное электрическое поле индуцируетсятакжев направлении оси z. Известно, что при такой ориентации полей МЭ коэффициент имеет максимальную величину, и влияние размагничивающего поля минимально[1, 2]. В этом случае уравнение (2) можно переписать, используя формулы (1) и (5) следующим образом
mS10 + zm/R1=ms11 mT1 + mq11 mp
mS10 + (zp- hm) /R1 =ps11 pT1 + pd31 pE3 ; (5)
Для выполнения условия равновесия погонные осевые силы в слоях структуры должны в сумме равняться нулю,
![]() (6)
(6)
где 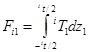 , mt иpt – толщины пьезомагнитного и пьезоэлектрического слоев. Далее, необходимо решить уравнение (5) относительно iTj и подставить в уравнение (6). Подстановка уравнений (2) , (6) в уравнение (4), позволяет найти mS10:
, mt иpt – толщины пьезомагнитного и пьезоэлектрического слоев. Далее, необходимо решить уравнение (5) относительно iTj и подставить в уравнение (6). Подстановка уравнений (2) , (6) в уравнение (4), позволяет найти mS10:
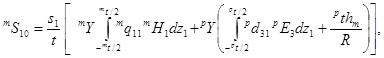 (7)
(7)
где s1=t(mtmY+ptpY+stsY)-1, t=mt+pt, mYиpY– модули упругости пьезомагнитной и пьезоэлектрической компонент.
В условиях равновесия моменты погонных осевых сил в слоях структуры должны уравновешиваться результирующей изгибных моментов Mmj, Mpj, возникающих в пьезоэлектрическом и магнитострикционном слоях в расчете на единицу ширины слоя.Таким образом,
Fm1hm +Fp1(hm+hp) = Mm1+ Mp1 +Ms1, (8)
Fm2hm +Fp2(hm+hp) = Mm2+ Mp2 +Ms2,
где 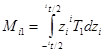 и
и 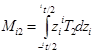 .
.
Учитывая уравнения (4), (5) и (7), а также условие равновесия (8), можно найтирадиус изгиба R. Для вычисления деформаций нейтральной оси, значения радиуса кривизны нужно подставить в уравнение (8). После того, как деформации определены, из уравнения (5) можно найти осевое напряжение iT1. Чтобы получить выражение для МЭ коэффициента по напряжению, воспользуемся условием разомкнутой цепи на границе раздела слоев:
D3=0 (9)
Очевидно, что D3 равно нулю для любого z, поскольку электрическая индукция является бездивергентной и имеет только одну компоненту D3. В данном случае уравнения (1) и (8) приводят к выражению для МЭ коэффициента по напряжению
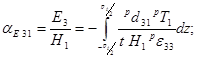 (10)
(10)
где E3 и p – среднее значение электрического поля, индуцируемогов пьезоэлектрическом слое, и внешнее переменное магнитное поле. Механическое напряжениеpT1 находится из уравнений (5) и (7).
2 Результаты моделирования магнитоэлектрического эффекта
Результаты расчета МЭ коэффициента α=U/p (U–индуцируемое напряжение) для слоистой структуры состава метглас – биморфный пьезоэлектрический преобразователь на основе ЦТС приведены на рис. 3. На этом же рис. приведены результаты расчета МЭ коэффициента для двухслойной структуры состава метглас – ЦТС. В расчетах использовались следующие материальные параметры:pd31=-270·10-12 м/В , pε33 /ε0 =3250; ps11= 15.3·10-12 м2/Н; mq11= 1.81·10-8 м/А; ms11= 10·10-12 м2/Н.
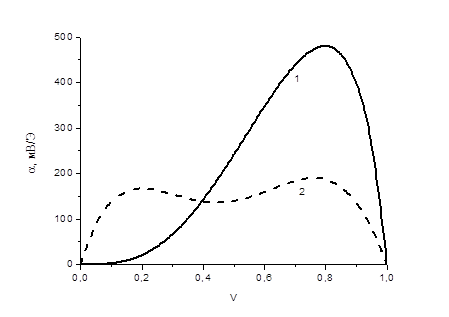
Рис. 3. Зависимость МЭ коэффициента от объемной доли пьезоэлектрика для слоистых структур состава: 1 - метглас – биморфный пьезоэлектрический преобразователь на основе ЦТС; 2 - метглас - ЦТС
Из рис. 3следует, что зависимость МЭ коэффициента от объемной доли пьезоэлектрика имеет вид кривой с двумя максимумами, что связано с наличием изгибных деформаций двухслойного образца [2].Использование биморфного пьезоэлектрического преобразователя в составе магнитострикционно-пьезоэлектрической структуры вместо однородного пьезоэлектрического слоя позволяет увеличить максимальное значение МЭ коэффициента с 190 мВ/Э до 480 мВ/Э. При этом объемная доля пьезоэлектрика, соответствующая максимуму α увеличивается с 0.77 до 0.8.
К достоинствам магнитострикционно-пьезоэлектрической структуры на основе биморфного пьезоэлектрического преобразователя следует отнести устойчивость по отношению к внешним аксиальным механическим напряжениям вследствие компенсации наводимых электрических напряжений в слоях биморфного преобразователя. Поэтому описанную магнитострикционно-пьезоэлектрическую структуру рекомендуется использовать при проектировании помехоустойчивых датчиков магнитного поля.
Заключение
В данной работе рассмотрена модельМЭ эффекта в магнитострикционно-пьезоэлектрических структурах на основе пьезоэлектрического преобразователя. На примере слоистой структуры состава метглас – ЦТС показано, что использование биморфного пьезоэлектрического преобразователя в составе магнитострикционно-пьезоэлектрической структуры вместо однородного пьезоэлектрического слоя позволяет увеличить максимальное значение МЭ коэффициента с 190 мВ/Э до 480 мВ/Э. Исследованная структура обладает устойчивостью по отношению к внешним аксиальным механическим напряжениям, что позволяет рекомендовать ее для использования при проектировании помехоустойчивых датчиков магнитного поля.
Работа выполнена при частичной финансовой поддержке Министерства образования и науки РФ в рамках государственного заказа.
Рецензенты:
Захаров А.Ю., д.ф.-м.н., профессор, заведующий секцией кафедры общей и экспериментальной физики ИЭИС «НовГУ», г. Великий Новгород;
Селезнев Б.И., д.т.н., профессор, заведующий кафедрой ФТТМ ИЭИС «НовГУ» г. Великий Новгород.



