Метод вариационногогенетического программирования сравнивался с методом генетического программирования [3] ипоказал свою эффективность при решении задачи синтеза оптимального управления. Методом вариационного генетического программирования решено несколько задач синтеза управления, в частности, задача оптимальной парковки мобильного робота из различных начальных условий с учетом пространственных ограничений [1]. Настоящая работа посвящена продолжениям исследований метода вариационного генетического программирования для синтеза систем управления. В работе рассматривается популярная для мобильных роботов задача синтеза оптимального управления движением вдоль пространственной траектории. Особенностью задачи является необходимость получения одной системы управления, обеспечивающей точное движение робота по различным пространственным траекториям.
Задача синтеза управления движением вдоль пространственной траектории
Рассмотрим формальную постановку задачи синтеза управления траекторным движением. Задана математическая модель объекта управления.
, (1)
где 
- вектор состояния объекта, 
- вектор управления, 
, 
,
- замкнутое ограниченное множество, 
.
Задана область начальных условий
. (2)
Заданы 
пространственных
траекторий движенияв форме 
-мерных
многообразий
, 
,
. (2)
Траектории (2) называем пространственными, так как они не зависят от времени.
Вместе с траекториями (2) заданы также начальная и конечная точки
, 
,
, 
,
, . (3)
Необходимо найти управление в форме
, (4)
где 
- искомая синтезирующая функция, 
, удовлетворяющая следующим свойствам:
·
, 
;
·
решение 
системы 
должно
обеспечивать минимум функционалуи удовлетворять условиям попадания в начальную
и конечную точки траектории
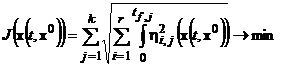, (5)
, 
,
. (6)
В качестве технической стратегии реализации системы управления, обеспечивающей движение по траектории, зададим точки на каждой заданной траектории
, . (7)
где
, , (8)
,
, , (9)
- заданная величина, определяющая
количество точек 
на траектории 
, .
Система управления движением объекта по траектории представляет собой систему стабилизации объекта относительно заданной точки из множества (7) с дополнительным условием переключения точек.
Для системы стабилизации относительно пространственной точки синтезирующая функция (4) в качестве аргумента должна использовать отклонение от заданной целевой точки
, (10)
В данном случае система управления должна дополнительно включать подсистему переключения целевых точек, например, по условию ее достижения или по истечении некоторого заданного промежутка времени
, если 
, (11)
где 
и 
-
заданные положительные величины, определяющие точность и скорость движения по
траектории.
Для решения задачи (1-6) синтеза системы управления движением объекта по пространственной траектории со стратегией (7)-(11) стабилизации относительно точек траектории используем метод вариационного генетического программирования [1], [3].
Пример синтеза системы управления движением по траектории
В качестве примера рассмотрим задачу синтеза системы управления движением мобильного робота по заданным пространственным траекториям.
Математическая модель объекта управления имеет следующий вид
, 
,
, (12)
где 
- постоянный параметр объекта.
Управление объектом ограничено в виде
, 
. (13)
Для системы (12) задано множество начальных условий
. (14)
Заданы пространственные траектории в виде
, . (15)
В качестве траекторий рассматривались 
траектории,
две из которых были гладкими, а две – с разрывами по производным.
Синтез системы управления выполнялся методом вариационного
генетического программирования. Рассматривалась стратегия управления
стабилизации точек траектории. При вычислительном эксперименте были приняты
следующие значения параметров модели и задачи: 
,
, 
,
, 
,
, 
,
, 
,
, 
,
, 
,
, 
,
, 
,
, 
,
c.,
, 
.
В результате синтеза была получена следующая синтезирующая функция:
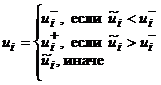, (16)
где
,
,
, 
,
,
, 
,
, 
.
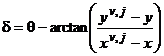На рис 1-4 приведены графики движения мобильного робота с полученным управлением по заданным пространственным траекториям. Там же приведены целевые точки траекторий, помеченные маркерами.
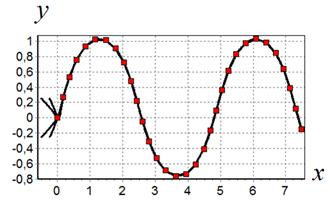
Рис. 1.Движение робота по траектории 1
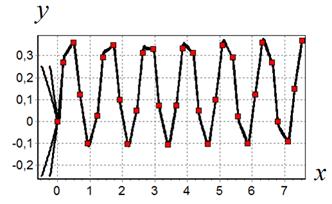
Рис. 2. Движение робота по траектории 2
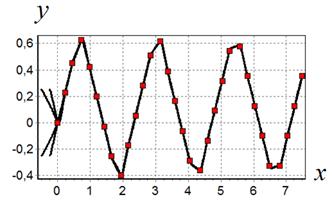
Рис. 3. Движение робота по траектории 3
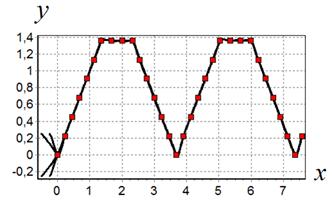
Рис. 4. Движение робота по траектории 4
Как видно из результатов моделирования полученная нелинейная система управления обеспечивает достаточно качественное движение робота по заданным пространственным траекториям. Точность прохождения целевых точек траектории достаточно высока. Начальные условия практически не влияют на качество управления.
Работа выполнена по гранту РФФИ № 14-08-00008-а.
Рецензенты:Никульчев Е.В., д.т.н., профессор, проректор по научной работе НОУ ВПО Московский технологический институт, г. Москва;
Демидова Л.А., д.т.н., профессор кафедры вычислительной и прикладной математикиФГБОУ ВПО Рязанский государственный радиотехнический университет, г. Рязань.