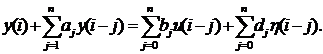
Учитывая, что оценивание параметров регрессионного–авто–регрессионного объекта (РАР–объект), частным случаем которого является временной ряд [1], осуществляется на основе последовательно поступающих данных, наиболее привлекательными методами оценивания параметров являются рекуррентные методы оценивания [2, 5]. Основной недостаток традиционного рекуррентного подхода состоит в том, что вне зависимости от времени поступления вся накопленная информация участвует в процедуре оценивания с одинаковыми весами. Очевидно, даже при медленно меряющихся параметрах, такой подход не приемлем. Хорошо известный в настоящее время метод экспоненциального взвешивания не дает желаемых результатов, так как обладает высокой чувствительностью к выбору весового коэффициента, учитывающего степень «старения» информации. Применение методов стохастической динамической фильтрации сопряжено с необходимостью использования дополнительной информации о динамике изменения параметров временного ряда, а также информации о статистических характеристиках шумов, действующих в идентифицируемой системе. В этой связи имеет смысл рассмотреть рекуррентный алгоритм, основанный на использовании только последних N измерений.
В настоящей работе предлагается рекуррентный алгоритм оценивания параметров линейного РАР – объекта по скользящей выборке заданного объема.
Пусть РАР – объект представлен в дискретно-разностной форме
,
где
– значения «выхода» и «входа»
идентифицируемого объекта в момент времени i,
параметры объекта 
–
подлежат идентификации, шум 
имеет следующие статистические
характеристики [3]:
,
,
— символ Кронекера.
Оптимальная настраиваемая модель [4], обеспечивающая несмещенные, состоятельные в средне – квадратичном оценки параметров РАР–объекта имеет вид [3]:
.
Введем вектор наблюдений «входа» модели
и вектор оценок параметров
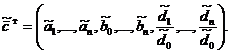
Тогда уравнение модели можно переписать в векторной форме:
.
Как отмечено
выше, будем искать оценку параметров по N (N
(n+(n+1)+n)) последним
измерениям. Причем, на каждом шаге рекуррентного процесса добавляется l новых измерений, а l старых выводятся из процесса
идентификации.
Тогда на 
шаге процесса идентификации матрица «входов»
U(k) может быть представлена в
виде блочного объединения двух матриц:
–U0(k) – матрицы размерности [(l) x (n+(n+1)+n)], которая будет удалена на следующем k+1 шаге процесса идентификации;
– U1(k) – матрицы размерности [(N-l) x (n+(n+1)+n)], которая будет сохранена на следующем k+1 шаге процесса идентификации.
Таким образом, матрица U(k) имеет блочный вид
,
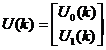очевидно, размерность этой матрицы будет [(N) на (n+(n+1)+n)].
С другой стороны, матрица «входов» U(k+1) на шаге k+1 также может быть представлена в виде объединения двух матриц:
– U2(k+1)= U1(k) – матрицы размерности [(N-l) x (n+(n+1)+n)], которая сохранена с предыдущего k-того шага процесса идентификации;
– U3(k+1) – матрицы размерности [(l) x (n+(n+1)+n)], которая будет добавлена на k+1 шаге процесса идентификации.
В результате матрица U(k+1) будет иметь вид
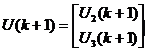или 
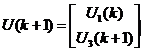(1)
Строками матриц 
являются транспонированные вектора 
в соответствующие моменты времени.
Аналогичным образом можно сформировать блочные вектора «выхода» на k и k+1 шагах процесса идентификаци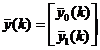и:
и
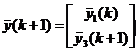
Вектора «выхода»
имеют тот же смысл, что и соответствующие
матрицы «входа».
Как известно [2,3], при использовании метода наименьших квадратов оценка параметров линейного объекта по N измерениям, с учетом введенных обозначений, на k-том и k+1-ом шагах процесса идентификации будет иметь вид:
; (2)
, (3)
Введем вспомогательную
оценку 
, вычисленную на основе матрицы «входа» 
и вектора «выхода» 
. (4)
– матрицы весовых коэффициентов
соответствующих размерностей. Естественно, для существования единственности
решения необходимо выполнение условия 
.
Обозначим
;
;
;
;
;
Используя эти обозначения, формулы для оценок (2), (3), (4) можно записать в виде:
; (5.а)
; (5.б)
(5.в)
Учитывая, что
матрицы 
, 
и
вектор 
являются блочными, и, осуществляя
несложные матричные преобразования, можно получить следующие рекуррентные соотношения:
(6.а)
(6.б)
или, используя соотношения (5а), последнюю формулу можно переписать в виде:
(7)
Применяя известное матричное тождество
для обращаемых матриц [2], выражение для матрицы 
можно
записать в виде:
.
(8)
Подставляя выражения (7) и (8) в формулу (5в) и произведя элементарные матричные преобразования, получим рекуррентную формулу для вспомогательной оценки
(9)
Повторяя
аналогичные рассуждения для матрицы 
и вектора 
, получим:
(10)
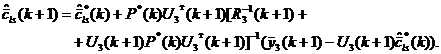(11)
Для задания
начальных значений 
можно воспользоваться обычной
формой метода наименьших квадратов при достаточном объеме «входных» и
«выходных» параметров с использованием упрощенной модели «объекта»
идентификации.
Ниже приведен двухступенчатый
алгоритм расчета оценок параметров 
. При формировании
алгоритма полагали, что коррекция результатов расчета производится на каждом
шаге измерительного процесса, т.е. l=1 (в
этом случае номер рекуррентного процесса k
совпадает с номером измерений i,
пересчет оценок происходит при каждом новом поступлении данных). В дальнейшем
при формировании алгоритма, в зависимости от контекста, будем использовать либо
индекс i, либо индекс k. Кроме того, как уже отмечалось, необходимым
условием единственности оценки является условие: 
.
Алгоритм
1.
Задание начальных значений 
Так
как значения «выхода» модели пока неизвестны, то принимаем упрощенный вид
модели:
; 
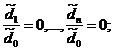
очевидно, в данном случае имеем 2n+1
оцениваемых параметра. Следовательно, для задания начальных условий достаточно
накопить 2n+1 последовательных
значений «входа» и «выхода».
1.1. Формируем матрицу «входов» 
и вектор «выходов» 
, i=[-2n, -2n+1,…,0],
,
.
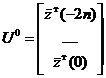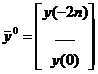1.2. рассчитываем начальные значения оценок:
, 
;
2.
Определение оценок параметров по упрощенной модели, 
.
2.1.
Формируем
матрицу «входа» и вектор «выхода», используем при этом упрощенный вид модели: 
, а 
.
2.2.
Рассчитываем
оценку и матрицу 
:
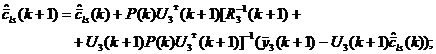
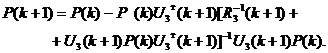
2.3.
Рассчитываем
значения «выхода» модели, используя её упрощенный вид. Расчет осуществляется по
формуле: 
эти значения запоминаются.
2.4.
Для
выполняем рекурсию 
и переходим
к п.2.1
3.
Определение оценок параметров оптимальной настраиваемой
модели для моментов 
.
На этом интервале можем использовать полный вид оптимальной настраиваемой
модели:
однако при этом еще не достигли заданного объема скользящей выборки.
3.1.
Формируем
матрицу «входа» и вектор «выхода», используем при этом полный вид модели:
.
3.2.
Рассчитываем
оценку и матрицу ,
используем при этом формулы, аналогичные приведенным в п. 2.2.
3.3.
Рассчитываем
значения «выхода» модели: 
эти значения запоминаются.
3.4.
Для
выполняем рекурсию 
и
переходим к п.3.1.
4.
Определение оценок параметров оптимальной настраиваемой модели
для моментов 
,
т.е. достигли заданного объема скользящей выборки.
4.1.
Формируем
матрицу «входа» 
и вектор «выхода» 
, которые должны быть выведены из
процесса идентификации:
.
4.2.
Формируем
промежуточные оценки параметра 
и матрицы 
:
4.3.
Формируем
матрицу «входа» 
и вектор «выхода» 
, которые вводятся на текущем шаге в
процесс идентификации:
.
4.4.
Рассчитываем
оценку и матрицу , при
этом используем формулы, аналогичные приведенным в п. 2.2.
4.5.
Рассчитываем
значения «выхода» модели:
эти значения запоминаются.
4.6.
Пока
поступают новые данные «входа» и «выхода» выполняем рекурсию и
переходим к п.4.1.
5. Конец алгоритма
Очевидно,
предлагаемый рекуррентный метод оценки параметров информационных потоков, представленных
в виде числовых потоков, по скользящей выборке заданного объема не дает каких –
либо преимуществ в плане точности оценки и объема хранимой информации по
сравнению с обычной формой метода наименьших квадратов. Однако, использование
предлагаемого метода дает возможность избежать кропотливой процедуры обращения
матриц. Как известно, порядок обращаемой матрицы в МНК равен числу оцениваемых
параметров. При использовании предлагаемого рекуррентного метода порядок обращаемой
матрицы равен числу обновленных данных l. В
случае, когда пересчет параметров происходит при каждом новом поступлении
данных 
, обращаемая матрица вырождается в скаляр.
Таким образом, использование предлагаемой модификации рекуррентной формы метода наименьших квадратов для оценки параметров формализованной модели данных позволяет устранить трудоемкую процедуру обращения матриц, с одной стороны, и учесть нестационарный вид модели, с другой.
Рецензенты:Загребаев А.М., д.т.н., профессор, Национальный исследовательский ядерный университет, г.Москва;
Кулябичев Ю.П., д.т.н., профессор, Национальный исследовательский ядерный университет (МИФИ), г. Москва.