Задача нахождения геометрического места режущих кромок боковой поверхности зуба точной гиперболоидной передачи является достаточно сложной задачей. Так, по мнению профессора Гавриленко В.А. вряд ли можно изготовить колесо на гиперболоидной заготовке из-за непреодолимых технологических трудностей [2]. Именно поэтому такие передачи не изготавливаются в промышленности.
Сложность изготовления гиперболоидных передач объясняется тем, что помимо переменной по ширине колеса аксоидной поверхности, впадина и толщина зуба должна быть переменными [1]. Кроме того, изменяется и угол наклона зуба.
Возможности современного высокопроизводительного оборудования с числовым программным управлением, в том числе и зубообрабатывающего оборудования, позволяют преодолеть технологические трудности, присущие традиционным методам зубообработки.
Для изготовления точной гиперболоидной передачи актуальной задачей является расчет и определение геометрического места режущих кромок при формообразовании боковых поверхностей зубчатого колеса.
Участки режущих кромок, формообразующих боковую поверхность зубьев гиперболоидной передачи в процессе резания представляют собой производящую поверхность. Взаимное расположение участков режущих кромок инструмента при нарезании боковой поверхности колеса можно исследовать графическими методами, в том числе в CAD/CAE пакетах по расположению линий пересечения режущих кромок инструмента с различными плоскостями: перпендикулярными к оси вращения одного из колёс, перпендикулярными к одной из координатных осей и т.д. (рис.1).
В представленном на рисунке 1 фрагменте имитационного кинематического формообразования боковых поверхностей зубьев гиперболоидного зубчатого колеса в среде Siemens NX воспроизводилось закоординированное вращение гиперболоида 1 и 2, по геометрическим характеристикам в представленном случае соответствующее единичному передаточному отношению. Формообразующие кромки 2, связанные с «управляющим» гиперболоидом 1 закоординированно перемещались в направлении линии пересечения делительных гиперболоидов. Шаг определялся исходя из заданных числа зубьев, а соответственно и проекции окружного шага на линию пересечения гиперболоидов, а также из условия постоянства шага. С учетом изменения геометрии зуба в сечениях от горлового до периферии, длина и угловое положение образующих менялись. Кинематические параметры и геометрические положения режущих кромок (образующих) управляются гипотетическим гиперболоидом 1, воспроизводящим зацепление с гиперболоидом 3.
Для расчета координат производящих линий боковой поверхности зуба использовался метод сечений. Расчёт координат линий пересечения производящих кромок с различными
плоскостями достаточно объемен, при относительно однотипных алгоритмах, связанных с преобразованием координат и его целесообразно проводить либо с использованием специально написанных программ на алгоритмических языках, либо с использованием математических пакетов, таких как Matlab.
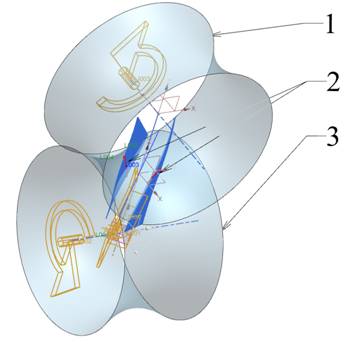
Рис.1. Имитация кинематики формообразования боковых поверхностей зубьев гиперболоидного колеса: 1 – гипотетический делительный гиперболоид, на основе которого осуществляется управление движением режущих кромок инструмента; 2 – образующие профиля линии (обработка при повышенных требованиях по точности предполагается раздельной); 3 – делительный гиперболоид обрабатываемого колеса
Аналитический вывод выполнен для частного случая формообразования боковых поверхностей гиперболоидного зубчатого колеса (общий случай излагается в работе [5]), рассчитанного на единичное передаточное отношение при угле скрещивания осей 90 градусов (рис.2). В отличие от известного метода определения координат производящих линий [5], расчет сопряженных производящих поверхностей был выполнен в параметрическом виде, учитывая, что в качестве производящей линии выбран отрезок прямой. Так как делительные гиперболоиды являются телами вращения, расчет производился для пространственной трансляции отрезка образующей, относительно гиперболоидов, участвующих в передаче. Для каждого гиперболоида сопряженные поверхности необходимо рассчитывать отдельно. Рассмотрим только для колеса 1. Для колеса 2 выкладки будут идентичными. С гиперболоидами свяжем неподвижные системы координат x1y1z1O1, x2y2z2O2. Гиперболоиды представляют собой поверхности вращения гипербол, уравнения которых в параметрическом виде имеют вид:
![]()
![]() ,
,
где a – действительная; b – мнимая полуоси гиперболы; i – номер гиперболоида и соответствующей системы координат.
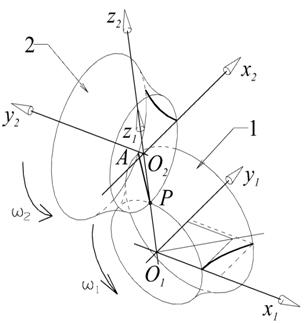
Рис. 2. Делительные гиперболоиды передачи
Гиперболоид 1 представляет собой делительный гиперболоид обрабатываемого зубчатого колеса. Гиперболоид 2 воспроизводит движение зубчатого колеса, работающего в паре с колесом 1, но при этом, с ним связана образующая (режущая кромка), формирующая профиль боковой поверхности зуба на гиперболоиде 1.
Рассмотрим движение режущей кромки инструмента в системе координат x2y2z2O2 (рис. 3). Так как образующая является отрезком прямой (в предположении, что режущая кромка не изменяет геометрии в процессе работы), достаточно рассмотреть движение двух ее точек: M1 и M2. Каждая из точек участвует в двух движениях – вращении вокруг оси y2 с постоянной угловой скоростью w2 (переносное движение), и движении по гиперболе вдоль y2 с постоянной проекцией скорости на ось y2 (относительное движение).
Крайние точки режущей кромки M1 и M2 соответственно соотносятся с участками гиперболоида (нижней части, ножки) зуба колеса 1 - точка M1, и области вершины зуба колеса 1 – точка M2. Каждая из точек движется в относительном движении по своей гиперболе, ограничимся рассмотрением точки М1.
![]()
![]() , при этом
, при этом ![]() .
.
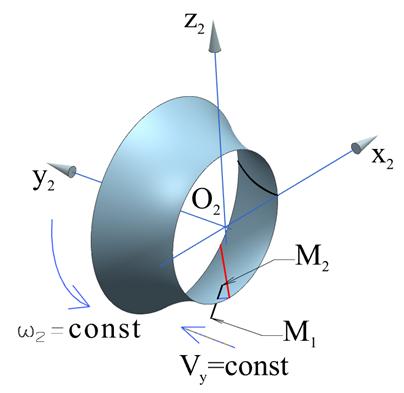
Рис. 3. Схема к расчету движения режущей кромки
В переносном движении точка вращается вместе с гиперболоидом. Ее угловое положение относительно оси x2, в плоскости, параллельной плоскости x2O2z2 определиться уравнением:
![]() ,
,
где ![]() - начальное
угловое положение точки М1.
- начальное
угловое положение точки М1.
Отсюда, для того чтобы рассчитать координаты точки M1, совершающей сложное движение, т.е. задать в зависимости ее координаты в параметрическом виде в системе координат инструмента имеем следующие зависимости, представленные матрицей:
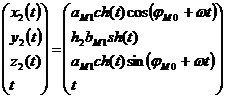 ,
,
где h2 – коэффициент шага винтовой линии.
При изменении параметра t матрица позволяет вычислить координаты точки M1 в системе координат x2y2z2O2, для этого задаются начальным значением и диапазоном изменения t, а также шагом, с которым можно осуществлять расчет, обеспечивая необходимую точность. Чтобы получить координаты производящей линии, участвующей в формообразовании боковой поверхности обрабатываемого колеса 1 (рис. 3), примем во внимание, что «инструмент» - колесо 2 вращается относительно колеса 1 с постоянной угловой скоростью w1. Координаты линии, образуемой на поверхности зуба обрабатываемого колеса точкой режущей кромки инструмента, при изменении t, будут иметь координаты, подсчитанные по зависимостям перехода от системы координат x2y2z2O2 к системе координат x1y1z1O1, относительно которой, указанная в начале система координат участвует в равномерном вращательном движении с угловой скоростью w=w1. Для рассматриваемого случая (рис.3) будут иметь место следующие соотношения:
![]() ;
;
![]() ;
;
![]() .
.
|
|
|
|
а) |
б) |
|
Рис.4. К расчету винтовых линий, вдоль которых формируется зуб а) постоянство шага винтовой линии; б) Совпадение направлений нормалей винтовых линий контактирующих зубьев на делительном гиперболоиде и их сонаправленность линии контакта гиперболоидов |
|
Данные соотношения применимы для компоновки, представленной на рис.3. Передаточное отношение равно единице, угол перекрещивания осей 90 градусов:
Для расчета, как соотносятся угловая скорость вращения зубчатого колеса и скорость поступательного движения проекции скорости точки М1 образующей на ось вращения колеса рассмотрим рис. 5, А). Зубчатое колесо имеет заданное число зубьев Z. При повороте на угол 360°/Z, проекция точки M1 на линию PA должна сместиться на величину шага P*. Данный шаг должен оставаться постоянным, несмотря на то, что диаметр увеличивается по закону гиперболы, соответственно меняется модуль при постоянном числе зубьев, что и учтено в приведенных соотношениях. Но это приводит к «деформации» боковых поверхностей зубьев в направлении от горлового сечения к торцовым.
Аналогично осуществляем расчет траектории движения точки М2 образующей M1M2, для моделирования боковой поверхности колеса 1. Затем, используя тот же подход, строим сопряженную поверхность для колеса 2. В данном случае колесо 2 считаем неподвижным, и обкатываем вокруг него «инструмент» - колесо 1, управляющий положением по жестким кинематическим зависимостям положением «режущей кромки» M1M2.
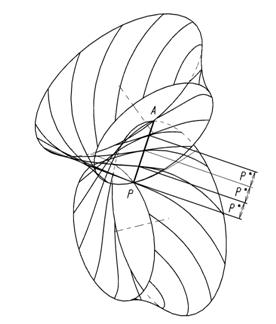
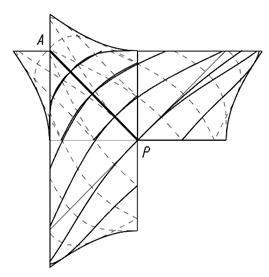
Таким образом, используя рассчитанные данные получили две боковые поверхности сопряженных боковых поверхностей зубьев гиперболоидной передачи (рис.5). Достоверность расчета была подтверждена имитационным зацеплением боковой поверхности зубчатых колес.
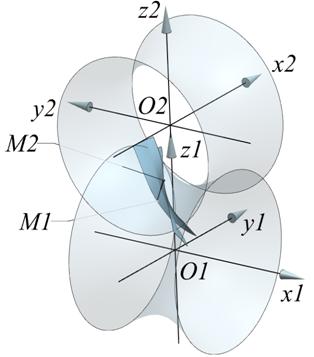
Рис. 5. Модели боковых поверхностей зубьев гиперболоидной передачи
Рецензенты:Лунев А.Н., д.т.н., профессор кафедры «Технологии машиностроительных производств» ФГОУ ВПО Казанского национального исследовательского технического университета им. А.Н. Туполева Минобрнауки РФ, г. Казань;
Шамсутдинов Ф.-Р.А., д.т.н., профессор, заведующий кафедрой «Общеинженерные дисциплины" ФГОУ ВПО Казанского государственного аграрного университета Минсельхоза РФ, г. Казань.




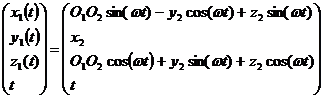 .
.