При работе в реальных условиях детали машин испытывают, как правило, переменные нагрузки различного типа, начиная от циклических нагружений с постоянной величиной и продолжительностью циклов нагружения и заканчивая нагружениями, в которых амплитуды и периоды нагружения принимают случайные значения. В настоящее время для оценки величины повреждения в основном используется правило линейного суммирования повреждений, где величина повреждения при i-ом режиме равна ni об / Ni, где ni об - общее число циклов нагружения за время действия нагрузки, при котором число циклов до разрушения равно Ni [9]. Это правило, однако, не для всех режимов нагружения достаточно адекватно отражает процесс накопления повреждений, носящий вероятностный характер [1, 5, 6].
Цель исследования
Определение правила накопления повреждений при переменных нагрузках для деталей, малонагруженных на первом этапе жизненного цикла. К таким деталям, в частности, можно отнести детали машин, прошедших приработку на режимах, когда возникающее напряжение далеко от напряжений, вызывающих усталостные повреждения.
Экспериментальная часть
Проверка полученных теоретических зависимостей проводилась по экспериментальным данным [7].
Результаты и обсуждения
Линейному правилу суммирования повреждений соответствует схема накапливающихся мгновенных повреждений, изображенная на рис.1, где N01 и N02 - число циклов до разрушения при различных нагрузках. Линии 0-1 и 0-2 отвечают средней скорости накопления повреждений, М – величина накопленного повреждения, при котором наступает отказ.
При безразмерной величине накопленных повреждений можно принять М = 1, а условие отказа
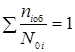, (1)
где niоб – общее число циклов нагружения при i-ом режиме, N0i – число циклов до разрушения при i-ом режиме.
При этом предполагается, что вероятность каждого следующего повреждения не зависит от числа ранее полученных повреждений.
Схеме накапливающихся повреждений отвечает гамма-распределение числа циклов безотказной работы, которое при большом числе повреждений приводит при данной схеме накопления повреждений к нормальному закону распределения числа циклов до разрушения 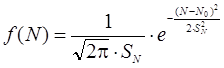[2].
, (2)
где N0 – математическое ожидание числа циклов до отказа; SN – среднее отклонение числа циклов до отказа.
Однако в случае, когда развитие процесса, приводящего к отказу, можно представить в виде произведения последовательных независимых случайных величин (например, рост трещины), применяют логарифмически-нормальное распределение [3, 8].
В отличие от схемы формирования механизма нормального закона последовательный характер случайных воздействий таков, что случайный прирост, вызываемый каждым следующим воздействием, пропорционален уже достигшему к этому моменту значению исследуемой величины.
Поэтому усталостные испытания приводят чаще всего к логарифмически-нормальному закону распределения числа циклов до отказа:
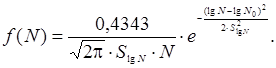(3)
Этому закону распределения соответствует схема накопления повреждений, изображенная на рис.2. Постоянство средней скорости накопления повреждений в логарифмических координатах означает, что средняя скорость накопления повреждений убывает с ростом числа циклов. Уменьшение скорости накопления повреждений может рассматриваться как отражение процесса упрочнения, протекающего наряду с разупрочнением, и создающего препятствия возникновению новых усталостных повреждений.
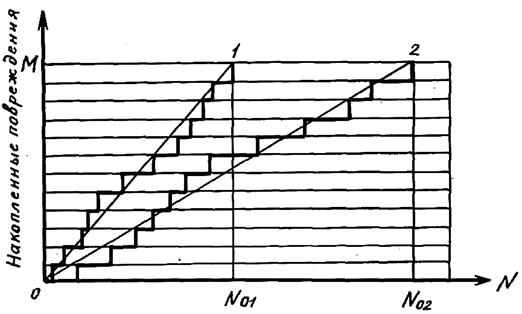
Рис. 1. Схема накопления повреждений (линейное правило суммирования)
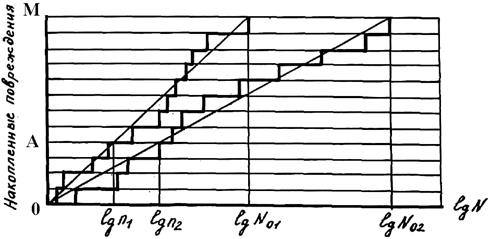
Рис.2. Схема накопления повреждений (логарифмическое правило суммирования)
При линейном законе суммирования повреждений 
приращение повреждений при i-ом режиме составит:
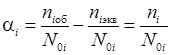, (4)
где niоб – общее эквивалентное число циклов с учетом i-го режима;
niэкв – общее эквивалентное число циклов, соответствующее i-му режиму, наработанное до i-го режима;
ni – число циклов нагружения при i-ом режиме нагружения;
N0i – число циклов до разрушения при i-ом режиме.
При логарифмическом законе приращение повреждения составит
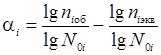, (5)
где niоб = niэкв + ni .
Из зависимостей (4) и (5) видно, что при логарифмическом законе суммирования, в отличие от линейного, величина повреждения зависит не только от числа циклов работы при данном режиме ni , но и от наработанного до этого режима числа циклов при других режимах niэкв .
Исходя из схемы накопления повреждений, представленной на рис.2, видно, что величина повреждения после первого режима 
может в безразмерных величинах может быть определена по формуле:
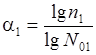, (6)
где n1 – число циклов нагружения при первом режиме, N01 – число циклов до разрушения при 1-ом режиме.
Величину одинакового повреждения А при различных режимах (рис. 2) при величине накопленного повреждения, соответствующего отказу М = 1, можно оценить по формуле:
(7)
Исходя из (6) и (7), число циклов при 2-ом режиме нагружения эквивалентно по величине нанесенного повреждения 1-му режиму:
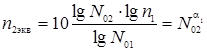, (8)
где дополнительно N02 – число циклов до разрушения при 2-ом режиме.
Величина повреждений после второго нагружения 
исходя из (7) и (8)
, (9)
где n2 + n2экв – приведенное число циклов 2-го режима нагружения, соответствующее 1-му и 2-му режимам нагружения.
При i-ом режиме нагружения величина повреждения
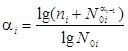, (10)
где 
- величина повреждения, накопленная при (i-1)-ом режиме.
Для определения эквивалентного числа циклов нагружения при i-ом режиме niэкв воспользуемся зависимостями (7) и (8):
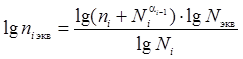. (11)
Для определения числа циклов до отказа при различных режимах нагружения можно использовать кривую усталости материала (рис. 3), устанавливающую взаимосвязь между максимальными напряжениями i-го режима нагружения 
и числом циклов до отказа N0i при данных напряжениях.
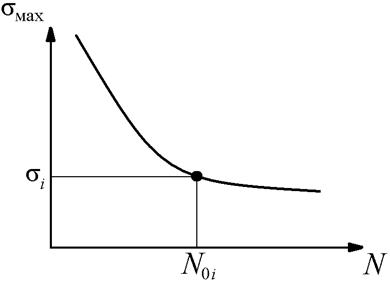
Рис. 3. Кривая усталости материала
Для аналитического описания кривой усталости используется степенное уравнение:
, (12)
где m – коэффициент, зависящий от материала, условий нагружения и геометрических параметров деталей.
Исходя из (13) число циклов до отказа при i-ом режиме N0i может быть определено по зависимости
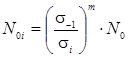, (13)
где 
- предел ограниченной выносливости, N0 = 107 - базовое число циклов для определения предела выносливости для сталей.
Число N0 = 107 циклов принимают за базовое, так как считается, что если стальной образец выдержал 107 циклов, то он выдержит практически неограниченное число циклов [4].
При величине накопленного повреждения, определенного по формуле (10) равной 1 должен наступить отказ.
Проверку зависимости (10) при отказах, вызванных контактной усталостью зубчатых передач, проводили по данным В.П. Мурашко [7].
В таблице указаны рассчитанные по линейному и логарифмическому закону суммарные повреждения, соответствующие отказу. Близость накопленного повреждения, соответствующего отказу к 1, рассчитанного по логарифмическому закону, показывает, что этот закон несколько лучше, чем линейный, описывает процесс накопления повреждений. Нужно отметить, что логарифмически нормальный закон распределения числа циклов до отказа, а значит, и логарифмический закон суммирования повреждений лучше работает при сравнительно малом числе циклов до отказа.
Таблица
Проверка логарифмического закона суммирования усталостных повреждений
|
№ испытания |
1 |
1 |
2 |
3 |
4 |
4 |
5 |
|
|
1,1 |
0,889 |
0,519 |
0,904 |
0,905 |
0,797 |
0,642 |
|
|
1,008 |
0,994 |
0,957 |
0,996 |
0,995 |
0,987 |
0,971 |
Заключение
Исследование показало, что логарифмический закон суммирования усталостных повреждений может быть использован для расчета накопленных повреждений и оценки долговечности деталей машин, прошедших приработку, в условиях малоцикловой усталости.
Рецензенты:
Луконин В.П., д.т.н., профессор, генеральный директор ФГУП «НИИ полимеров им. В.А. Каргина», г. Дзержинск;
Сажин С.Г., д.т.н., профессор, генеральный директор НТЦ АСТ, г. Дзержинск.