Современные тенденции выработки тепловой и электрической энергии экологичными и экономичными способами обусловили разработку и применение в энергетике теплонасосных систем и установок [4,2]. Но для их эффективного использования необходим анализ тепловых режимов водоемов с теплообменником-испарителем теплового насоса. При решении такого рода задач целесообразно учитывать особенности течения жидкости в режиме смешанной конвекции. Известны результаты численного моделирования сопряженного конвективно-кондуктивного теплопереноса в прямоугольной газовой области при наличии источника тепловыделения [3,6-8]. Но моделирование конвективных течений в водоеме в условиях сложного теплообмена с окружающей средой, а также притоков и стоков тепла, до настоящего времени не проводилось. Поэтому целесообразным является математическое моделирование смешанной конвекции вязкой несжимаемой жидкости в прямоугольной области с локальным стоком тепла и с источниками ввода и вывода массы.
Для решения задачи конвективного теплопереноса рассматривалась прямоугольная полость (с теплообменником-испарителем теплового насоса), имеющая участки ввода и вывода жидкости и одну свободную поверхность (рис. 1).
При моделировании предполагалось, что теплофизические свойства жидкости и материала стен не зависят от температуры. Жидкость считалась теплопроводной, вязкой, ньютоновской, удовлетворяющей приближению Буссинеска. Режим течения – ламинарный, границы полости (за исключением участков ввода и вывода воды) – непроницаемы. Не учитывался отток массы за счет испарения со свободной поверхности. В начальный момент времени принималось, что температура во всей рассматриваемой области постоянна и одинакова.
Эти допущения не вносят в постановку задачи значительных ограничений, но позволяют упростить ее решение. Температура теплообменника-испарителя остается неизменной в течение всего процесса.
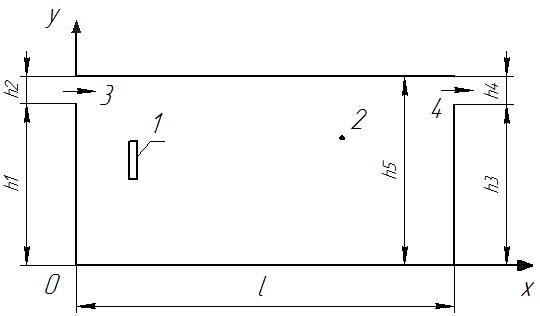
Рис. 1. Область решения задачи: 1) теплообменник-испаритель, 2) водоем, 3) участок ввода жидкости, 4) участок вывода жидкости
На участке ввода массы (рисунок 1) горизонтальная скорость принимается постоянной, на выходе из полости приняты условия симметрии по продольному направлению.
Отметим, что в реальных водоемах возможна реализация трехмерных распределений температур и компонент скоростей, но в рассматриваемой задаче поперечная составляющая скорости будет меньше двух других компонент, соответствующих основной плоскости (X,Y) движения вводимой в резервуар воды. Поэтому можно считать принятое допущение о двухмерной постановке задачи обоснованным.
Процесс переноса тепла в жидкости (рисунок 1) для принятой физической модели описывается системой нестационарных двухмерных уравнений Навье-Стокса в приближении Буссинеска с нелинейными граничными условиями [ 7]. Задача решалась в безразмерной постановке.
|
|
(1) |
|
|
(2) |
|
|
(3) |
здесь 
- число Грасгофа; g– ускорение, создаваемое массовыми силами; β - температурный коэффициент объемного расширения; ν - коэффициент кинематической вязкости жидкости; L – характерный размер полости; 
- число Рейнольдса; 
- число Прандтля; а - коэффициент температуропроводности; 
-безразмерная температура;
Начальные условия имеют вид:
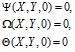
Граничные условия:
– на внешних границах (кроме верхней) области заданы условия теплоизоляции:
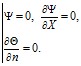при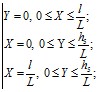 
– на верхней границе жидкости задано условие «свободной поверхности»:
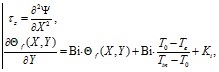при 
– на входе в полость:
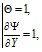при 
– на выходе из полости:
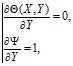при 
,
– на границах теплообменника: 
.
здесь 
– число Био; 
– безразмерное касательное напряжение; 
– безразмерное число испарения; 
– касательное напряжение на свободной поверхности; 
– динамическая вязкость жидкости; 
– коэффициент теплообмена между внешней средой и рассматриваемой областью решения по границе
; 
– температура окружающей среды; 
– коэффициент теплопроводности жидкости; 
- массовая скорость испарения; 
– температура испарения; 
– давление насыщения; 
– парциальное давление испаряющихся компонентов; 
– газовая постоянная; 
– теплота фазового перехода; А – коэффициент аккомодации; М – молекулярный вес.
Решение уравнений (1–4) с соответствующими начальными и граничными условиями реализовано методом конечных разностей на равномерной сетке. При решении задачи использовался алгоритм [1,3,5,7], разработанный для численного решения задач естественной конвекции в замкнутых прямоугольных областях с локальными источниками энергии. Моделирование осуществлялось в среде Matlab.
Численные исследования проведены при следующих значениях безразмерных величин, соответствующих режиму смешанной конвекции: 
, и температур: 
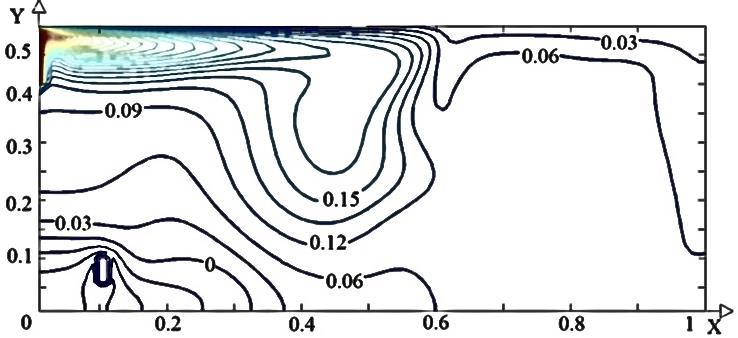
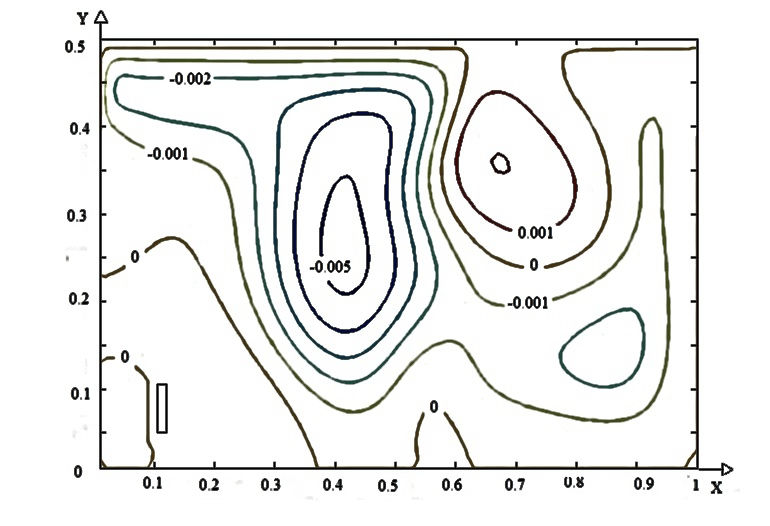
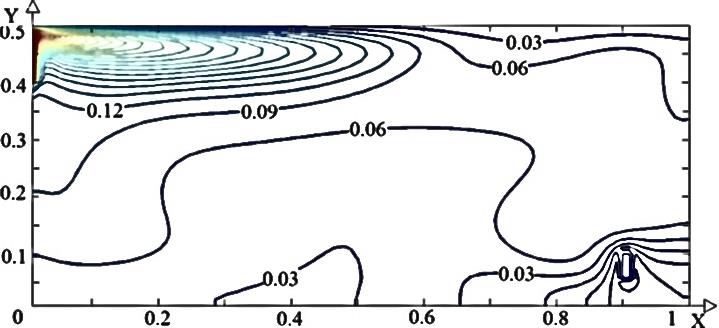
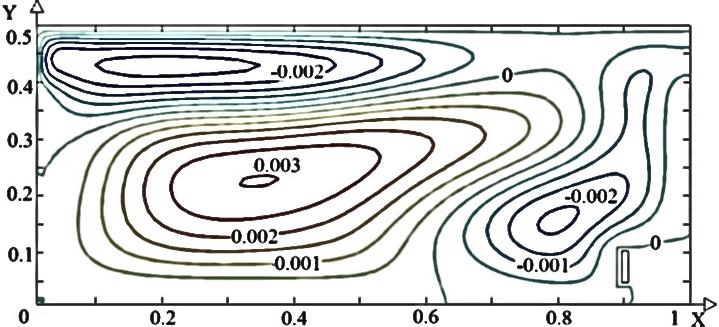
На рисунке 2 представлены линии тока и поле температур, характеризующие режим смешанной конвекции вязкой несжимаемой жидкости в прямоугольной области для различных вариантов положения теплообменника-испарителя теплового насоса в водоеме. Установлено, что при расположении испарителя в нижней левой части водоема (рис. 2 а, б) формируются два центральных вихря. Холодная масса воды, циркулирующая около стока тепла не перемешивается с основным потоком жидкости. В результате формируется застойная зона, что приводит к уменьшению интенсивности теплообмена испарителя с окружающей жидкостью.
|
|
|
|
|
а |
б |
|
|
|
|
|
|
в |
г |
|
|
|
|
|
|
д |
е |
|
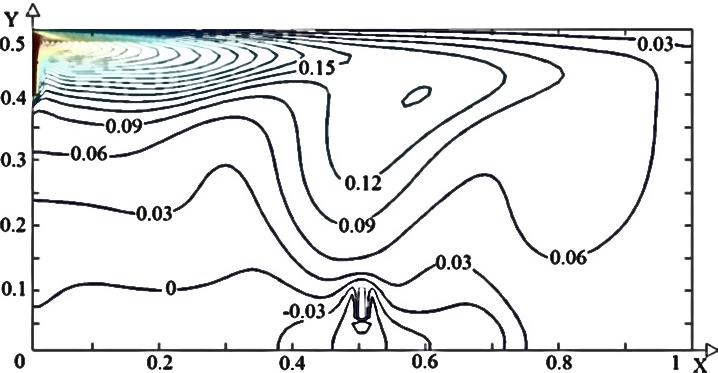
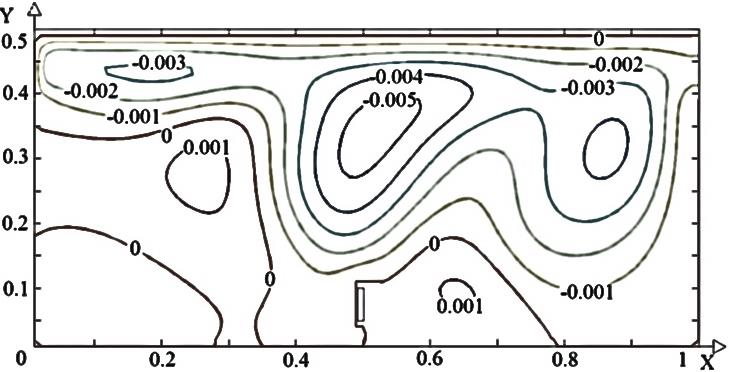
Рис. 2. Поле температуры (а, в, д) и линии тока (б, г, е) для различных положений теплового насоса (1 – а, б; 2 – в, г; 3 – д, е)
При расположении стока тепла в нижней центральной зоне (рис. 2 в, г) два основных вихря смещаются к правой стенке за счет образования вторичных вихрей в левой области. Теплообмен между жидкостью и испарителем интенсифицируется, так как последний находится в области основного вихря, что приводит к отсутствию обширных застойных низкотемпературных зон. Распределение температуры в этом случае достаточно равномерно по всему объему водоема. Смещение испарителя к правой стенке (рис. 2 д, е) делает возможным образование трех обширных вихрей. Основной вихрь располагается в центре, другой в области ввода жидкости (высокотемпературный), третий у теплообменника (низкотемпературный).
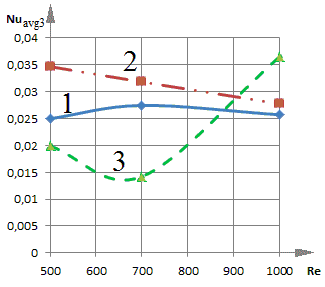
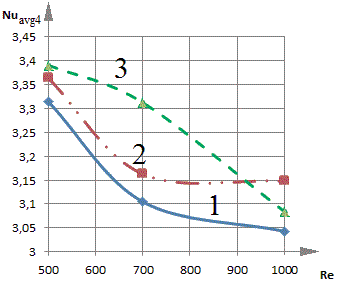
Проведен анализ влияния числа Рейнольдса на значения среднего числа Нуссельта на трех границах полости и свободной поверхности жидкости:
(рисунок 3 а), 
(рисунок 3 б),
(рисунок 3 в), 
(рисунок 3 г).
|
|
|
|
в |
|
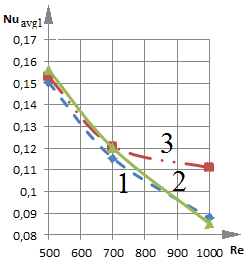
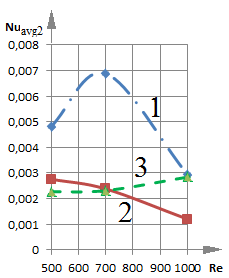
Рис. 3. Зависимость среднего числа Нуссельта от числа Рейнольдса при различном расположении теплообменника-испарителя теплового насоса.
Видно (рис. 3), что с увеличением числа Re на границах Х = 0 и Y = 1 (рис. 3 а, г) происходит снижение значений безразмерного коэффициента теплообмена для всех вариантов расположения теплообменника испарителя.
Следует отметить, что расположение теплового насоса в левой и средней части водоема препятствует развитому циркуляционному течению по центру водоема. В тоже время зависимости Nuavg = f (Re) для границ Х = 1 и Y = 0 области решения при крайнем левом и крайнем правом размещении теплообменника отличаются своей немонотонностью. Наблюдаются точки излома (рис. 3 б, в). Такое расположение стока тепла при низких скоростях ввода воды препятствует продвижению потока жидкости с температурой Θ = 1 к соответствующим угловым зонам рассматриваемой области и контакту с прилегающими стенками. Но при увеличении циркуляционных течений достигаются достаточные для перетока части энергии жидкости за испаритель, расположенный слева (рис. 2 а, б), условия. Температуры выравниваются, в результате интенсивность теплообмена снижается (зависимость 1 на рис. 3 б, в). Расположение теплообменника справа (рис. 2 д, е) препятствует движущемуся теплому потоку жидкости достигать нижней части границы Х = 1. Это обстоятельство оказывает влияние на средний коэффициент теплообмена (рис. 3 а, г).
Также стоит заметить, что числа Нуссельта на свободной поверхности водоема (Nuavg) (рис. 3 г) значительно выше. На твердых границах Nuavg не превышает 0.16, на свободной же – среднее число Нуссельта достигает 3.3. На границе жидкости Y = 1 осуществляется интенсивный отток теплоты, но с увеличением числа Рейнольдса диапазон изменений значений среднего по этой границе числа Нуссельта незначителен.
Можно отметить, что зависимости Nuavg = f (Re) изменяются при разных схемах размещения теплообменника-испарителя. Можно сделать вывод, что при смене положения стока тепла в водоеме соответственно изменяются и температурные режимы.
Сформулированная модель смешанной конвекции жидкости в водоеме, используемом в качестве низкопотенциального источника энергии испарителя теплового насоса, с локальными участками ввода и вывода массы может быть использована для усовершенствования методики расчета тепловых режимов водоемов – источников низкопотенциальной теплоты.
Работа выполнена в рамках НИР Госзадания «Наука» (Шифр Федеральной целевой программы 2.1321.2014).
Рецензенты:
Борисов Б.В., д.ф.-м.н., профессор каф. Теоретической и промышленной теплотехники НИ ТПУ, г. Томск;
Голдаев С.В., д.ф.-м.н., с.н.с., профессор каф. Теоретической и промышленной теплотехники НИ ТПУ, г. Томск.