Рассматриваются актуальные для разработки тренажных и обучающих комплексов (для подготовки операторов наземных, воздушных, надводных транспортных средств) вопросы объективизации оценки оператором эргатической системы характеристик объекта по его управляемости [1…4]. Предполагается справедливость гипотезы о стационарности параметров объекта, описываемого уравнением движения вида (режим стабилизации):
|
|
(1) |
Матрицами ![]() и
и ![]() полностью определяется объект управления;
полностью определяется объект управления;
![]() ,
, ![]() ,
, ![]() .
.
Характеристики объекта определяются через инварианты матрицы ![]() (собственные числа
(собственные числа ![]() , след матрицы
, след матрицы ![]() ,
, ![]() ); ими же определяются решения системы S:
); ими же определяются решения системы S:
|
|
(2) |
При
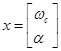 ,
, 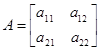 ,
, 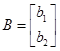
в зависимости от инвариантов ![]() (
(![]() ) и
) и ![]() определяются 12 качественно различных систем (объектов управления):
определяются 12 качественно различных систем (объектов управления):
1. ![]() ,
,
2. ![]() < 0, ∆<0;
< 0, ∆<0;
3. ![]() ,
,
4. ![]() < 0, ∆=0;
< 0, ∆=0;
5. ![]() > 0, ∆=0;
> 0, ∆=0;
6. ![]() = 0, ∆=0;
= 0, ∆=0;
7. ![]()
![]()
8. ![]() > 0, ∆=
> 0, ∆=![]()
![]()
9. ![]() = 0, ∆=0;
= 0, ∆=0; ![]()
10. ![]() < 0, ∆>
< 0, ∆>![]()
11. ![]() > 0, ∆>
> 0, ∆>![]()
12. ![]() = 0, ∆>
= 0, ∆>![]() .
.
Здесь собственные числа ![]() .
.
Оценка качества объекта производится по функционалу качества
|
|
(13) |
Последние два слагаемых ограничивают собственные частоты колебаний объекта как сверху, так и снизу; вторым слагаемым определяется уровень колебательности. Система ![]() тем лучше, чем меньше величина
тем лучше, чем меньше величина ![]() ;
;![]() - весовые константы. Выбор весовых констант осуществлялся на основе анализа корреляционных связей [5] между
- весовые константы. Выбор весовых констант осуществлялся на основе анализа корреляционных связей [5] между ![]() и инвариантами
и инвариантами ![]() (возможно использование итеративного способа).
(возможно использование итеративного способа).
Естественно рассматриваются лишь экспоненциально устойчивые системы с инвариантами, удовлетворяющими условиям ![]() <0; ∆>0 (системы 1,7, 10).
<0; ∆>0 (системы 1,7, 10).
В выбранной N-балльной шкале система ![]() принадлежит классу k тогда и только тогда, когда ее инварианты
принадлежит классу k тогда и только тогда, когда ее инварианты ![]() , где области на плоскости
, где области на плоскости ![]() (геометрическая интерпретация классов), определяются в соответствии с функционалом (3).
(геометрическая интерпретация классов), определяются в соответствии с функционалом (3).
Для неколебательных систем (случаи 1 и 7) функционал (3) представляется в виде
|
|
(4) |
а для колебательных систем (случай 10) с собственной частотой
|
|
(5) |
в виде
|
|
(6) |
Рассмотрим неравенство
|
|
(7) |
Для неколебательных систем с учетом
![]()
из (4) следует
![]()
или
|
|
(8) |
Откуда из
![]()
следует
|
|
(9) |
Соотношение (7) эквивалентно
![]()
Откуда
|
|
(10) |
Искомые области ![]() равных оценок приводятся на рис.1
равных оценок приводятся на рис.1 ![]()
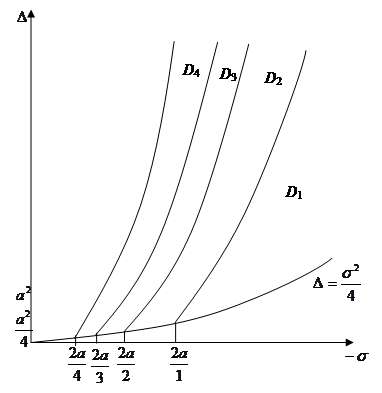
Рис.1.Области равных оценок для неколебательных систем
Для колебательных систем (7) имеет вид:
![]() .
.
С учетом ![]() имеем:
имеем:
![]()
Откуда
|
|
(11) |
Справедливо
|
( |
(12) |
Откуда следует
|
|
(13) |
Соотношение (11) эквивалентно
![]()
или
|
|
(14) |
В соответствии с (13), (14) области равных оценок (рис.2) для колебательных систем определятся границами:
- прямыми
![]() ,
,
- кривыми
|
Рис.2. Области равных оценок для колебательных систем Укажем и асимптотические представления неравенств (13), (14).
При
При
|
(15) |
Далее из (14)
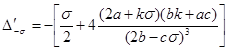 ,
,
откуда с учетом (12) и (13) следует
![]()
При ![]() функция
функция ![]() монотонно возрастает (рис. 1).
монотонно возрастает (рис. 1).
Займемся далее установлением областей равных оценок относительно инвариантов
|
|
(17) |
Очевидны соотношения
|
|
(18) |
Из (13), (14) следует
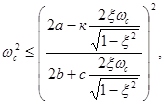
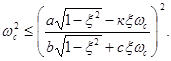
Откуда
|
|
(19) |
В силу ![]()
![]() 0 (19) равносильно
0 (19) равносильно
|
|
(20) |
|
|
(21) |
Рассмотрим неравенство
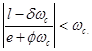
Оно равносильно
|
|
(22) |
Тогда (20) удовлетворяется при
|
|
(23) |
Из (23) следует
|
|
(24) |
|
|
(25) |
В силу ![]() >0 областью решения неравенства (24) (дискриминант
>0 областью решения неравенства (24) (дискриминант ![]() )
)
будет ![]() (при
(при ![]() решений нет);
решений нет); ![]() корни трехчлена
корни трехчлена ![]() .
.
Аналогично для неравенства (25)
![]() .
.
Так как для рассматриваемых систем ![]() то неравенство (25) решений не имеет, поэтому областью решений системы (24)-(25) будет интервал
то неравенство (25) решений не имеет, поэтому областью решений системы (24)-(25) будет интервал ![]()
Полученные области использовались для объективизации оценки оператором характеристик объекта в процессе управления, а также для оценки имитационных характеристик тренажных и обучающих комплексов по подготовке операторов на основе данных нормального функционирования двух систем: оператор - реальный объект, оператор-модель объекта [6…12].
Рецензенты:
Родионов Ю.В., д.т.н., профессор, директор автомобильно-дорожного института ПГУАС, профессор кафедры «Эксплуатация автомобильного транспорта», г. Пенза;
Кошев А.Н., д.х.н., профессор, профессор кафедры информационно-вычислительных систем Пензенского государственного университета архитектуры и строительства, г. Пенза.




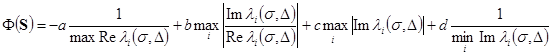 .
.
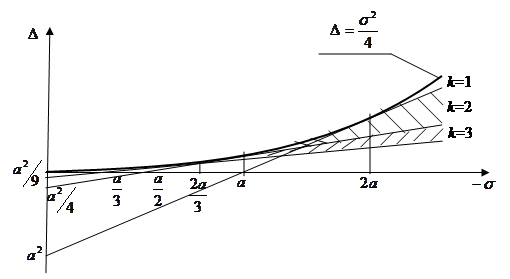
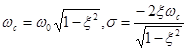 ,
,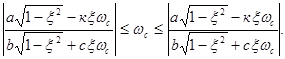
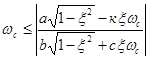 или
или 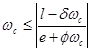 ;
;