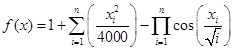Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Рассматривается наиболее общая задача безусловной оптимизации с параллелепипедными ограничениями (1)-(2):

(1)

(2)

В качестве тестовых функций в работе рассматривается небольшой набор функций с различными экстремальными характеристиками (табл.1)

Таблица 1

Набор тестовых функций

Поведение этих функций при представлено в виде карт линий уровня на рис. 1.

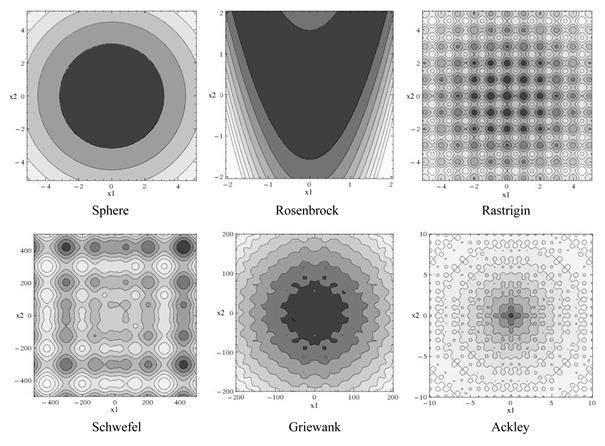
Рис. 1. Карты линий уровня тестовых функций ()

Как видно из рис. 1, первые две функции являются достаточно простыми для любого метода оптимизации, а оставшиеся четыре будут уже значительно сложнее, особенно при увеличении размерности.

1. Параметры эволюционного алгоритма

Стохастические методы глобальной оптимизации можно условно разделить на одноточечные и многоточечные (популяционные) методы. Популяционные методы в отличие от одноточечных оперируют множеством точек (популяцией). Частными случаями популяционных методов являются эволюционные алгоритмы, которые моделируют естественный отбор [1; 3]. Общая схема эволюционных алгоритмов показана на рис. 2.

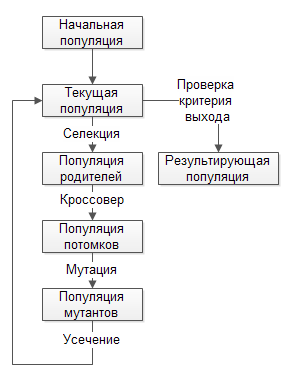
Рис. 2. Общая схема эволюционного алгоритма

В работе используется достаточно стандартный набор параметров алгоритма. В качестве оператора селекции выбран турнирный отбор [1; 5], оператора скрещивания – многоточечный кроссовер с точками разрыва [1; 2]. В новую популяцию отбирается наиболее приспособленных особей из родителей и их потомков, где – размер популяции. Конкретные значения параметров представлены в табл.2.

Таблица 2

Набор параметров эволюционного алгоритма

Как видно из табл.2 вероятность мутации установлена достаточно высокой и, таким образом, оператор мутации становится основным поисковым механизмом алгоритма. В работе рассмотрены следующие варианты операторов (табл. 3)

Таблица 3

Рассматриваемые операторы мутации

2. Вычислительные эксперименты

Для каждой функции из набора (табл.1) запуск алгоритма производится многократно с каждым из предложенных операторов мутации. Далее подсчитываются основные статистики по запускам: минимальное, максимальное и среднее значения, а также стандартное отклонение достигнутого в запуске минимума (табл.4). Число запусков для каждого оператора принято равным 100. Для обеспечения равных условий для операторов запуски производятся из одних и тех же случайно выбранных в области определения функции стартовых точек. В целях практического применения дальнейших результатов, размерность задач будем достаточно велика и равна 100.

Таблица 4

Результаты вычислительных экспериментов

Усредненные по 100 запускам результаты отложены в виде графиков на рис.3. По оси абсцисс указано число этапов генетического алгоритма (число поколений), по оси ординат – средняя приспособленность популяции. За одно поколение целевая функция вызывается 15 раз. По оси ординат указано значение достигнутого минимума.

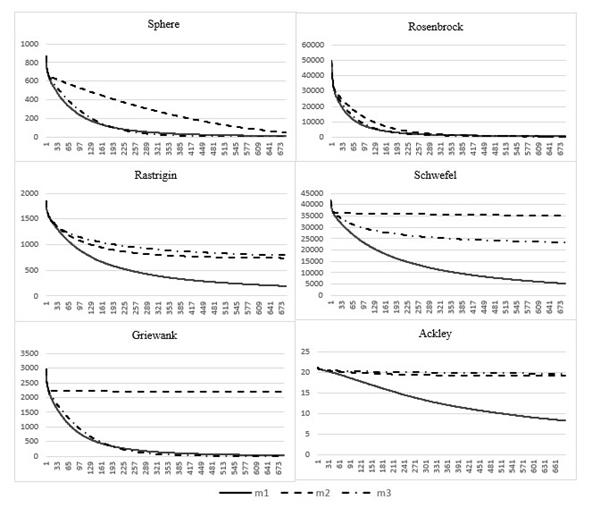
Рис. 3. Усредненные результаты запусков

На основе полученных результатов можно сделать следующие выводы:

1) на сложных многоэкстремальных функциях (Rastrigin, Schwefel и Ackley) оператор мутации показывает лучшие результаты;

2) на менее сложных функциях (Sphere, Rosenbrock и Griewank) операторы мутации и показывают похожие результаты, лучшие, чем у оператора .

Таким образом, глобальное изменение координат выглядит предпочтительнее изменения в небольшом шаре для всех функций тестового набора.

Для функций, отличающихся значительной сложностью рекомендуется более осторожное покоординатное изменение (оператор наподобие ). Для простых функций схожих результатов можно добиться как покоординатным (оператор наподобие ) так и полным изменением (оператор наподобие ).

Заключение

В данной статье произведено экспериментальное сравнение операторов мутации на наборе целевых функций. Показано преимущество операторов мутации с большим радиусом изменения, а также большая универсальность оператора, реализующего случайный выбор точки в шаре случайного радиуса с центром в точке , где .

Рецензенты:

Ширапов Д.Ш., д.ф.-м.н., профессор, ФГБОУ ВПО Бурятский государственный университет, г. Улан-Удэ;

Дамбаев Ж.Г., д.т.н., профессор, ФГБОУ ВПО Бурятский государственный университет, г. Улан-Удэ.