Доступность насаждения к освоению можно охарактеризовать проникаемостью, под которой понимается вероятность существования траектории перемещения машины из одной точки в другую, по условиям не пересечения определенной габаритной полосы движения и повреждения стволов произрастающих деревьев [3, 4].
Обзор работ в данном направлении [1, 4, 5] показывает, что неплохие результаты по определению проникаемости насаждения могут быть получены с помощью имитационного моделирования движения машины, с расхождением между теоретическими и экспериментальными данными не более 8 %. Однако применение существующих моделей для малогабаритных лесных машин не представляется возможным из-за их конструктивной специфики.
Рассмотрим модель движения малогабаритной одноосной машины с длинномерным грузом под пологом леса. Имитационную модель движения машины можно свести к решению задачи о плоскопараллельном движении твердого тела среди случайно распределенных препятствий, что подразумевает поэтапное решение следующих задач:
1. Генерирование пространственной структуры древостоя.
2. Математическое описание траектории движения максимально удаленных друг от друга двух точек машины, одна из которых, в соответствии с курсом теоретической механики, принимается за полюс.
В практике лесной таксации, при определении среднего расстояния между деревьями исходят из случайно-равномерного расположения деревьев на лесном участке. Поэтому, на первом этапе в декартовой системе координат генерируется п случайных точек с координатами (хi; yi), где i = 1, 2, ..., n. При этом некоторые точки могут оказаться в непосредственной близости друг к другу, так как их распределение на данном этапе совершенно случайно. Если точки рассматривать как деревья, то, учитывая законы естественного отбора, такая ситуация будет далека от реальности. В этом случае для более естественного расположения деревьев необходимо потребовать, чтобы каждое дерево было локализовано от своих соседей на определенном расстоянии, в результате чего и достигается случайно-равномерное распределение [2].
Для математического описания траектории движения машины представим ее в виде отрезка конечной длины, равного длине машины с грузом. Ширину (колею) машины, во избежание излишней громоздкости модели, удобнее задавать увеличенным на определенную величину диаметром деревьев [4].
Примем следующие допущения:
1) поворот происходит вокруг мгновенного центра скоростей, в качестве которого принимается вершинный отрез хлыста, на который опирается машина, а перемещение и скорость точек корпуса машины пропорциональны их удалению от точки опоры хлыста на опорную поверхность;
2) при повороте в области сцепки тягово-энергетического и грузонесущего модулей отсутствует степень свободы в горизонтальной плоскости;
3) при отсутствии препятствий движение машины параллельно оси ординат.
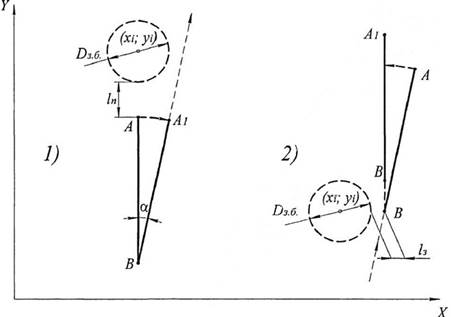
Рис. 1. Расчетная схема траектории машины при объезде дерева
Первое допущение принимаем для достижения естественной стратегии оператора по оцениванию возможной траектории движения заблаговременно до встречи с препятствием, при этом расстояние, остающееся между машиной и деревом, компенсирует занос хлыста при повороте и исключает пересечение необходимой зоны безопасности вокруг каждого дерева.
Второе допущение принимаем из-за сравнительно малого расстояния от вертикальной оси управляемых движителей до узла сцепки, с грузонесущим модулем по сравнению с общей длиной машины.
Третье допущение необходимо для минимизации траектории движения.
Моделирование движения производим следующим образом. При встрече с препятствием, машина заранее, не дожидаясь столкновения, начинает поворачивать на некоторый достаточно малый угол попеременно в обе стороны до тех пор, пока абсцисса точки А (начало машины) не совпадет сабсциссой, максимально удаленной от центра дерева точкой зоны безопасности и занимает положение со следующими координатами:
![]() (1)
(1)
![]() , (2)
, (2)
где ![]() и
и ![]() – абсцисса и ордината начала машины при повороте на угол
– абсцисса и ордината начала машины при повороте на угол ![]() , м;
, м;![]() и
и ![]() – абсцисса и ордината первоначального положения точкиА, м;
– абсцисса и ордината первоначального положения точкиА, м; ![]() – длина машины с грузом, м;
– длина машины с грузом, м; ![]() – угол поворота, град.
– угол поворота, град.
Затем, путем последовательного приращения ![]() машина начинает прямолинейное движение, при этом траектории начальной и конечной точек описываются уравнениями:
машина начинает прямолинейное движение, при этом траектории начальной и конечной точек описываются уравнениями:
![]() ; (3)
; (3)
![]() ; (4)
; (4)
![]() ; (5)
; (5)
![]() , (6)
, (6)
где (![]() ;
; ![]() ) – текущие координаты точекА и В, м; (
) – текущие координаты точекА и В, м; (![]() ;
; ![]() ) и (
) и (![]() ;
; ![]() ) – предыдущие координаты точек А и В, м;
) – предыдущие координаты точек А и В, м; ![]() – приращение по оси ординат, м.
– приращение по оси ординат, м.
Движение продолжается до совпадения ординат точки В и центра дерева, после чего происходит выравнивание машины до равенства абсцисс начала и конца машины. Далее, для минимизации длины траектории движения, машина последовательно поворачивает на малый угол в противоположную началу поворота сторону, одновременно передвигаясь вверх по оси ординат до тех пор, пока абсциссы точкиВ и вертикальной оси полосы движения не будут равны, при этом после каждого приращения проверяется условие допустимости нового положения.
В общем случае, при объезде препятствия, центр которого совпадает с траекторией движущейся параллельно оси ординат машины, расстояние, остающееся между машиной и зоной безопасности, максимально и определяется из следующего выражения:
![]() ; (7)
; (7)
![]() (8)
(8)
где ![]() – диаметр зоны безопасности, м;
– диаметр зоны безопасности, м; ![]() – расстояние, остающееся между машиной и деревом в момент принятия решения о необходимости поворота, м.
– расстояние, остающееся между машиной и деревом в момент принятия решения о необходимости поворота, м.
По мере удаления траектории движения от центра тяжести дерева ![]() убывает обратно пропорционально, достигая минимального значения при движении машины по касательной к препятствию, что позволяет в качестве диаметра зоны безопасности принимать сумму значений диаметра дерева и ширины (колеи) машины.
убывает обратно пропорционально, достигая минимального значения при движении машины по касательной к препятствию, что позволяет в качестве диаметра зоны безопасности принимать сумму значений диаметра дерева и ширины (колеи) машины.
Для реализации процесса движения машины в насаждении была составлена программа на языке программирования Delphi.
Целью имитационного моделирования является определение зависимости проникаемости насаждения от конструктивных параметров машины (длины, колеи) и таксационных характеристик древостоя (густоты, диаметра деревьев).
Для решения поставленной цели проведена серия активных многофакторных экспериментов. В качестве структурной модели матрицы планирования выбран полный факторный эксперимент типа 33.
Таблица 1
Уровни и интервалы варьирования факторов
|
Факторы |
Обозначение |
Уровни варьирования |
|||
|
натуральное |
кодированное |
-1 |
0 |
+1 |
|
|
Густота, шт./га |
п |
х1 |
300 |
450 |
600 |
|
Колея, м |
b |
х2 |
0,9 |
1,15 |
1,4 |
|
Длина машины, м |
L |
х3 |
5 |
9 |
13 |
Минимизация суммы квадратов, характеризующих расхождение между экспериментальными точками и значениями выходного параметра, вычисленными по уравнению регрессии, после исключения незначимых эффектов, позволила получить следующую регрессионную модель в натуральных обозначениях факторов:
![]() . (9)
. (9)
Адекватность модели исходным данным, близкий к 100 % коэффициент детерминации R = 98 % и сравнительно низкая ошибка выходного параметра Sе = 3 % дают все основания полагать, что полученная регрессионная модель имеет неплохие прогностические свойства, и ее использование для анализа доступности насаждения к освоению будет сопровождаться минимальным риском принятия ошибочного решения.
Рецензенты:
Самсонова И.В., д.э.н., доцент, главный консультант, Общество с ограниченной ответственностью «Малое инновационное предприятие «Агрикон», г. Якутск;
Исаев А.П., д.б.н., зав. лабораторией, лаборатория мерзлотного лесоведения Института биологических проблем СО РАН, г. Якутск.



