В общем виде, концептуально, процесс абразивной обработки можно представить в виде схемы, изображенной на рис. 1. Полупространство с заданными теплофизическими и механическими свойствами движется относительно неподвижной системы координат XYZ параллельно плоскости Х0У со скоростью Vк=(Vх; Vy). По поверхности полупространства движется развертка шлифовального круга со скоростью Vк, касаясь его по некоторому пятну контакта, которое является зоной шлифования. Зерна шлифовального круга, согласно современной концепции теории шлифования – дискретное множественное микрорезание, попадая в зону шлифования, становятся тепловыми источниками, инициируя нагрев материала заготовки [2, 5].
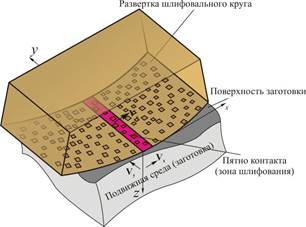
Рис. 1. Принципиальная схема теплофизики шлифования
Для математической реализации такой многофакторной расчетной схемы (нагрев трехмерного подвижного полупространства системой движущихся тепловых источников, действующих в локальной зоне поверхности полупространства) целесообразно применить известный методический подход к решению сложных задач – декомпозицию. В нашем случае предлагается следующая декомпозиция задачи: учет теплопередачи; кинематика и дискретность теплового источника; дифференциация единичных тепловых источников – зерен.
Расчетная схема для учета теплопередачи
На первом уровне разработки модели пренебрежем структурой теплоподвода и введем в зоне шлифования некоторый обобщенный тепловой источник интенсивностью 
. Тогда расчетная схема (см. рис. 1) приобретет следующий вид (рис. 2).
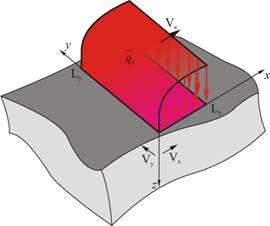
Рис. 2. Первый уровень формализации – теплопередача
Такой вид тепловой источник имеет в схеме сплошного контакта [7]. Т.е. зону контакта можно считать сплошным источником с плотностью теплового потока, распределенного по всей геометрической площадке контакта круга и заготовки по какому-либо непрерывному закону. С подходов аналитического описания и численного решения теплофизические модели со сплошным контактом являются наиболее удобными и простыми. Наряду с этим содержат «слабый» элемент – закон распределения плотности теплового потока в рассматриваемой зоне – определяется только исходя из экспериментальных исследований. Кроме того, эти модели базируются на целом ряде гипотез относительно закона распределения интенсивности теплового источника. Поэтому применимость этих моделей определяется и правомочностью базовых гипотез.
Такая расчетная схема приводит ко второй краевой задаче для уравнения теплопроводности в подвижной среде.
Расчетная схема учета кинематической дискретной структуры теплового источника
В учете теплопередачи (рис. 2) тепловой источник задан в общем виде, без учета его сложной кинематической структуры.
Для построения модели, учитывающей особенности теплоподвода при шлифовании, представляемого как множественное микрорезание, рассмотрим структуру теплоподвода – проведем второй уровень формализации.
Физически тепловой источник (в соответствие с базовыми положениями современной теории шлифования, сформулированными в работах Л.А. Глейзера [3] и С.Н. Корчака [9]) представляет собой множество единичных тепловых источников – абразивных зерен, которые перемещаются со скоростью Vк относительно зоны шлифования (рис. 3).
Каждый единичный тепловой источник – абразивное зерно имеет свою интенсивность тепловыделения qi , в соответствии с которой формируется температурное поле от воздействия данного единичного источника – зерна. Температурные поля от воздействия единичных источников накладываются друг на друга и образуют суммарное температурное поле зоны шлифования.
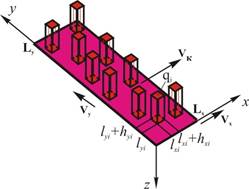
Рис. 3. Второй уровень формализации – дискретная кинематическая структура теплового источника
При этом интенсивности qi не являются независимыми. Согласно второму базовому положению теории обрабатываемости, предложенной С.Н. Корчаком [9], интенсивность каждого теплового источника – зерна зависит от температуры материала в момент врезания в него этого зерна (через прочностную температурно-скоростную характеристику материала). Поэтому учет кинематической дискретной структуры теплового источника обуславливает необходимость отработки обратной связи процесса шлифования и приведет к разработке, скорее всего, имитационного алгоритма.
Дифференциация единых тепловых источников
Согласно фундаментальным положениям процесса шлифования, вскрытым Л.А. Глейзером, источники теплоподвода – абразивные зерна, вследствии особенностей механики контактного взаимодействия при шлифовании, разделяются на режущие и трущие (давящие) абразивные зерна [3]. Анализ работ по изучению строения профиля шлифовального круга и его контакта с обрабатываемой поверхностью показал, что приблизительно 10–17 % являются режущими, а остальные в виду разновысотности профиля шлифовального круга – трущими (давящими) [1, 11]. При этом в видах шлифования, работающих по несвободной схеме резания, вследствие действия кинематических параметров управления, абразивные зерна – источники теплоподвода работают в разных зонах – резания (зона II) и выхаживания (зона I). Работа в разных зонах, предопределяет разный уровень интенсивности тепловых источников, в зоне резания – более мощный, в зоне выхаживания – меньшая интенсивность тепловых источников (рис. 5).
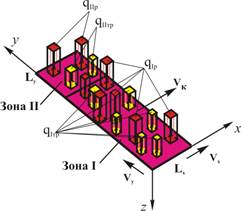
Рис. 5. Дифференциация тепловых источников и зон
Также следует учитывать, что абразивное зерно в свою очередь на микроуровне работает двумя поверхностями – передней, где происходит пластическая деформация снимаемых объемов обрабатываемого материала и задней, по которой происходит трение. При этом вследствие малых размеров абразивных зерен законом распределения теплового источника внутри каждой поверхности пренебрегаем и принимаем равномерным.
Однако очень важным вопросом является определение закона распределения сплошного источника (см. рис. 2). Поскольку рассматривается дискретная схема контакта, то данный закон распределения формируется воздействием множества единичных тепловых источников qi с постоянным законом распределения.
Величину каждой поверхности тепловыделения теплового источника qi (рис. 6) можно определить по зависимостям, предложенным С.Н. Корчаком [9].
Таким образом, источник является существенно неравномерным при переходе из зоны пластической деформации в зону трения.
Таким образом, имеем четыре множества зерен (qIр, qIтр, qIIр, qIIтр) с комбинацией из четырех микрозон тепловыделения (qIрS, qIтр, qIIрS, qIIтр), работающих в двух зонах тепловыделения – резания и выхаживания.
Интегральное решение обобщенной теплофизической задачи абразивной обработки
Для расчетной схемы учета конвективности теплопереноса при абразивной обработке имеем уравнение теплопроводности с конвективными членами [4, 5]:
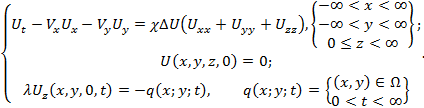(1)
где Ω – полуплоскость:
(2)
Это вторая краевая задача для уравнения теплопроводности в полупространстве в подвижной среде с конвективными членами. Для подобной задачи без конвективных членов существуют аналитические решения, в том числе функция Грина [8].
С помощью функциональных преобразований данную задачу можно свести к каноническому виду, т.е. исключить конвективные члены из уравнения, переведя их в свободный член через краевое условие. В данном случае таковым функциональным преобразованием может явиться:
(3)
В итоге, для функции 
задача (1) приводится к каноническому виду 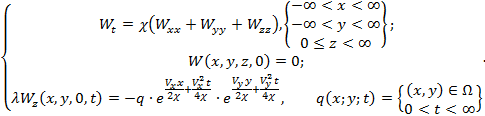(4).
(4)
Полученная система (4) – каноническая вторая краевая задача уравнения теплопроводности в полупространстве. Для этой задачи в математической физике существует функция Грина [10].
Возвращаясь к исходным переменным, получаем интегральное решение (1) – свертку функции Грина и плотности теплового источника 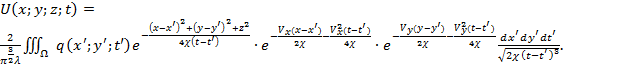(5).
(5)
Учитывая, что источник действует только в зоне шлифования, т.е.:
(6)
приходим к трехкратному интегралу 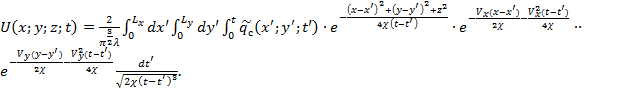(7).
<
(7)
Решения (7) кроме конвективности теплопереноса позволяют учесть и структуру теплового источника, т.к. функция его плотности распределения по зоне шлифования стоит в подынтегральном выражении. Для этого достаточно учесть, что в реалии тепловой источник 
имеет дискретную структуру: конечное множество зерен – источников мощностью qi движется по зоне Ωпк со скоростью круга Vк.
Приходим в конечном итоге, используя свойства аддитивности интегралов, к виду:
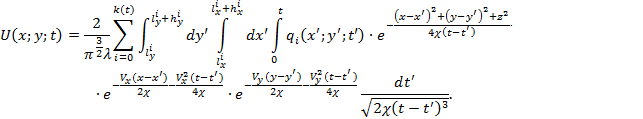(8)
Здесь интеграл берется по области Ωпк – но только по совокупности областей отдельных тепловых источников – зерен, т.е. интегрирование идет по всем отдельным областям Ωi.
Полученное уравнение (8) является общим интегральным решением второй краевой задачи для уравнения теплопроводности в подвижной среде с учетом дискретной кинематической структуры теплового источника для принципиальной теплофизической схемы шлифования.
Подынтегральное выражение в (8) описывает вклад в температурное поле зоны шлифования каждого зерна – источника, имеет смысл рассмотреть его для отдельного теплового источника и получить функцию влияния отдельного теплового источника – зерна (по аналогии с функцией Грина).
Рецензенты:
Бурнашов М.А., д.т.н., профессор кафедры «Конструкторско-технологическое обеспечение машиностроительных производств», ФГБОУ ВПО «Госуниверситет – УНПК», г. Орел;
Мазеин П.Г., д.т.н., профессор, профессор кафедры технологии машиностроения, ФГБОУ ВПО «Южно-Уральский государственный университет» (НИУ), г. Челябинск.