Одним из ключевых понятий междисциплинарного подхода к проектированию процесса обучения являются междисциплинарные знания, которые в профессиональном обучении играют важную роль в повышении уровня научно-теоретической и практической подготовки обучающихся [3]. Фундаментальность в подготовке дает возможность молодым специалистам в области экономики быстро адаптироваться в социальной среде и успешно применять профессиональные знания и умения в конкретных ситуациях при решении прикладных задач в научной и в профессиональной сферах деятельности. Как показывает практика, комплексное исследование и учёт междисциплинарных связей (МДС) уже на этапе проектирования методической системы обучения способствуют более полной реализации в учебном процессе дидактического потенциала образовательных технологий и педагогической продукции, функционирующей на базе информационных и коммуникационных технологий (ИКТ). Это позволяет заложить прочный научный фундамент в профессиональную подготовку будущих экономистов. Характерной чертой современного экономического образования является массовое использование технологии дистанционного обучения [1; 2]. В этой связи вопросы систематического исследования МДС рассматриваются нами как важное условие дальнейшего развития методической системы обучения математическим и экономическим дисциплинам.
Проблемы изучения междисциплинарных связей применительно к обучению в средней школе нашли отражение в исследованиях известных российских учёных: Федорца Г.Ф., Максимовой В.Н., Махмутова М.И., Шакирзянова А.З., Федоровой В.Н. и других авторов. Проблемой анализа междисциплинарных связей математики и химии занимались Александрова Т.К., Голобородько М.Я., Скатецкий В.Г.; математики и физики – Монахов В.М.; математики и биологии – Максимова В.Н.
В то же время в трудах отечественных ученых недостаточно полно исследованы механизмы установления и анализа МДС в профессиональной подготовке бакалавров экономики, опирающиеся на взаимосвязь и взаимопроникновение математических и экономических контекстов. Мало внимания уделяется также разработке прикладных методик учёта МДС естественнонаучных дисциплин (математика, физика, химия, биология) и экономических дисциплин (макроэкономика, эконометрика) при разработке учебно-методической документации.
Опираясь на ранее опубликованные работы, междисциплинарные связи будем понимать [2] как системное свойство педагогической системы, характеризующее интегративные качества целостной системы научных знаний проблемной области профессиональной деятельности и проявляющееся в формальном отображении междисциплинарных знаний этой области в структуре методической системы обучения базовым учебным дисциплинам.
Структура междисциплинарных знаний имеет сетевую, горизонтально-вертикальную организацию. Эта сеть состоит из девяти основных блоков: онтологическое знание; теоретическое; модельно-проективное; эмпирическое; практическое; обыденное; интерпретативное, математическое, метатеоретическое (рис. 1).
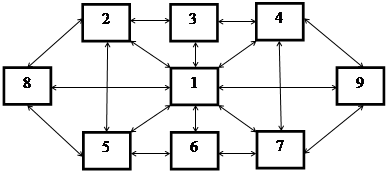
Рис.1. Структура знания в междисциплинарных науках
1) онтологическое – свойства и отношения экономической системы;
2) теоретическое – знания из экономической области (логически системное описание свойств, отношений и законов экономических объектов);
3) модельно-проективное – теоретические модели экономических систем, их описание, математические расчеты на функциональность, надежность, эффективность и др.;
4) эмпирическое – описание данных наблюдений и эксперимента, их систематизация и графическое оформление, формулировка фактов и законов поведения и функционирования экономических систем;
5) практическое – построение математической модели экономических объектов и систем;
6) обыденное – совокупность инструкций и предписаний по использованию математических моделей на практике;
7) интерпретативное – множество определений, связывающих элементы соседних уровней знания путем их отождествления (идентификации);
8) математическое – язык математических теорий, используемый для обработки экспериментальных данных, формулировки фактов, законов, принципов, констант, описания теоретических структур и их преобразований (формализованные математические теории; содержательные математические теории; математические проблемы и задачи; прикладные математические проблемы и задачи).
9) метатеоретическое – фундаментальное знание из естественных и социально-гуманитарных наук, математические теории, философские принципы и основания, этические, экономические и экологические регулятивы и ограничения, оценки социального и практического характера и др.
На рис. 2 показано представление междисциплинарных знаний с помощью диаграмм Эйлера – Венна для двух и трех предметных областей. На нем видно, что междисциплинарные знания представляют собой пересечение двух или более предметных областей, поэтому им присущи как признаки и особенности научных знаний этих областей, так и специфические признаки и особенности.
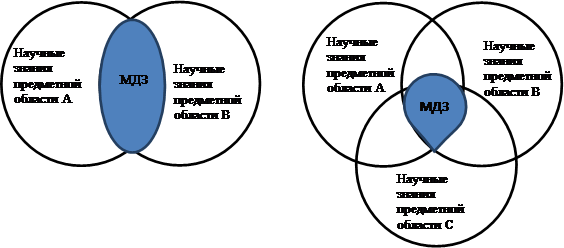
Рис. 2. Представление междисциплинарных знаний с помощью диаграмм Эйлера – Венна
К специфическим особенностям МДС (в МСО) следует отнести: распределённость; нестационарность; стохастичность; мультиколлинеарность; многофакторность; неопределённость; неоднозначность (в проявлении и оценке характеристик). Добавим также, что МДС в силу их природы и способа формального отображения следует отнести к группе плохо идентифицируемых объектов.
Примем допущение, что МДС выделяются и отображаются в МСО в соответствии с рекомендациями системного подхода к исследованию сложных явлений как структурно-расчлененной целостности, в которой каждый элемент структуры имеет определенное функциональное назначение. При этом структурные элементы (теории, разделы, темы, факты, понятия, законы) выделяются в каждой из интегрируемых предметных областей.
Создание теории и методологии информатизации образования (Ваграменко Я.А., Бешенков С.А., Гужвенко Е.И., Козлов О.А., Пак Н.И., Роберт И.В., Тихонов А.Н.), с одной стороны, и успехи в развитии теории информатики (Данилюк С.Г., Дараган А.Д., Поспелов Д.А.), с другой стороны, открыли новые возможности для изучения структуры и содержания МДС с позиции семантического подхода (Башмаков А.И., Кузнецов И.П., Надеждин Е.Н., Шихнабиева Т.Ш.). Одним из проявлений общей тенденции комплексного использования ИКТ и реализации основополагающих принципов информатизации образования является формирование информационно-образовательной среды (ИОС) (Касторнова В.А., Прозорова Ю.А., Роберт И.В.). По мнению ведущих учёных в области информатизации образования, инструментарий и сервисы ИОС образовательного учреждения, реализуя возросший дидактический потенциал ИКТ, сегодня должны рассматриваться в качестве перспективного средства осуществления междисциплинарного подхода при проектировании методического обеспечения дисциплин профессионального цикла.
В процессе нашего исследования установлено, что изучение МДС пересекающихся предметных областей должно быть направлено, прежде всего, на изучение их смысловых аспектов и вопросы идентификации в рамках базовых семантических моделей и схем.
Под семантическим анализом МДС будем понимать экстрагирование МДС в составе методической системы обучения студентов, идентификации основных показателей и классификации состояния МДС на некотором конечном множестве состояний [6].
Будем полагать, что основополагающими в семантическом анализе МДС являются следующие задачи.
1. Задача структуризации проблемной области знаний на содержательном уровне с выделением в ней предметных областей (концептов) и связей между ними. При этом осуществляется типизация МДС в соответствии с априорно известными классификационными признаками.
2. Задача идентификации, которая состоит в параметризации МДС с привлечением эвристических процедур ранжирования качественных признаков и в формальном представлении семантики отношений между концептами в базисе выделенной группы семантических сетей.
3. Задача классификации формальных объектов – семантических представлений МДС, заключающаяся в установлении смыслового содержания множества отношений между концептами, выражении его конечным набором признаков и в определении конкретного класса построенной семантической конструкции на принятой дискретной шкале. Решение задачи даёт оценку влияния МДС на результаты учебного процесса, что фактически определяет возможность корректировки компонентов МСО.
Первые две задачи ранее рассмотрены в работах [8; 9; 10]. Остановимся на третьей задаче семантического анализа МДС.
Введём следующие обозначения: 
– профессиональные компетенции (общепрофессиональные, проектная деятельность, организационно-управленческая деятельность); 
– профессиональная компетентность (аналитическая деятельность, научно-исследовательская деятельность); 
– общекультурные компетенции; 
– общее число запросов к системе междисциплинарной базы знаний; 
– интервал времени между моментом запроса и получением правильного ответа;
– число попыток решения задачи; 
– время активного поиска информации обучающимся. Тогда систему одновременных уравнений можно записать в следующем виде:
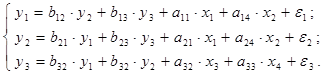(1)
В процессе обследования обучающихся на основе анкетирования, тестирования и метода экспертных оценок нами были получены следующие исходные данные (в баллах), которые представлены в табл. 1.
Таблица 1
Данные тестирования студентов
|
Периоды обучения |
|
|
|
|
|
|
|
|
1 2 3 4 5 |
10 11 15 15 18 |
7 10 10 12 16 |
12 13 13 15 19 |
14 13 12 14 10 |
1 1 2 2 3 |
10 8 9 5 5 |
1 2 3 2 3 |
|
|
20 |
20 |
20 |
15 |
5 |
15 |
5 |
В таблице 2 представлено соответствие баллов и времени для переменных 
и 
.
Таблица 2
Соответствие баллов и времени тестирования студентов
|
Переменная |
Переменная |
||
|
баллы |
время |
баллы |
время |
|
1 |
3–4 дн. |
1 |
более 5 ч. |
|
2 |
1–2 дн. |
2 |
3–4 ч. |
|
3 |
в течение дня |
3 |
2–3 ч. |
|
4 |
5–6 ч. |
4 |
1–2 ч. |
|
5 |
1–2 ч. |
5 |
в течение часа |
Система одновременных уравнений (1) является идентифицируемой, поэтому для её решения можно применить известный в математической статистике косвенный метод наименьших квадратов (МНК) [10]. В работах [4,9] рассмотрены методы решения систем одновременных уравнений.
Конечный результат идентификации аналитической модели имеет вид системы трёх линейных одновременных уравнений:
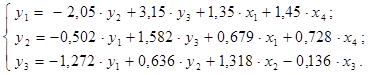
Таким образом, анализ построенной аналитической модели позволяет охарактеризовать характер и степень влияния параметров МДС на процесс формирования компетенций. Так, например, на профессиональные компетенции существенное влияние оказывают общекультурные компетенции, а влияние переменных 
и примерно одинаково. Формирование общекультурных компетенций, в свою очередь, в значительной степени зависит от влияния таких факторов, как интервал времени между моментом запроса и получением правильного ответа и профессиональная компетентность (аналитическая деятельность, научно-исследовательская деятельность).
Рецензенты:
Зайцева С.А., д.п.н., доцент, зав. кафедрой информационных систем и технологий Шуйского филиала ФГБОУ ВПО «Ивановский государственный университет», г. Шуя;
Гужвенко Е.И., д.п.н., доцент, доцент кафедры математических и естественнонаучных дисциплин Рязанского высшего воздушно-десантного командного ордена Суворова дважды Краснознаменного училища имени генерала армии В.Ф. Маргелова, г. Рязань.