Физические процессы в периодических структурах используются во многих устройствах микро и оптоэлектроники (дифракционные решетки, лазеры с распределенным брегговским отражением, направленные ответвители, фильтры на периодических структурах и др.). Физика процессов в этих структурах имеет много общего с квантовой физикой движения электронов в кристаллах, что позволяет пользоваться понятиями блоховских зон. Основной проблемой для практического использования периодических структур является сложность технологии их изготовления с необходимыми допусками на параметры сред и размеров. Кроме того, необходимо производство целого ряда элементов с различными параметрами для реализации устройств с различными характеристиками. В настоящей работе показана возможность создания периодической структуры с перестраиваемыми параметрами. Перестройка параметров может осуществляться уровнем поступающего сигнала, что обеспечивает высокую скорость перестройки. Задача о нахождении коэффициентов отражения и прохождения волны любой природы, падающей на ограниченную многослойную периодическую структуру, может быть решена при помощи различных модификаций матричного метода. Однако, получаемые решения хотя и точны по форме, но громоздки, что не позволяет провести детальный анализ физических свойств. Имеется лишь один вид двухслойных периодических структур с линейными параметрами сред - безграничные, для которых получено точное дисперсионное уравнение при любых соотношениях параметров волн и структуры. В данной работе методом построения волн Флоке-Блоха получены аналитические решения для коэффициентов отражения и прохождения волн от двухслойной периодической ограниченной диэлектрической структуры с учетом нелинейности параметров одного из слоев для плоской электромагнитной волны. Двухслойная периодическая прозрачная немагнитная среда с диэлектрическими проницаемостями слоев ε1 и ε2=ε2 +Χ(|E|2), и толщинами d1 и d2 занимает область пространства
0 ≤ z ≤ N(d1 + d2) = Nd,
где N- число периодов структуры, d1 + d2=d - период функции ε(z).
Диэлектрическая проницаемость сред кусочно-неоднородная, но однородная внутри каждого из слоев. Для E (Нx,Еy,Нz) волн (при ![]() ) поле может быть представлено как
) поле может быть представлено как
E(x,z,t) = E(z)exp(ikxx)exp(iωt),
где kx проекции волнового вектора k на ось 0x. Функция E(z) описывается уравнением:
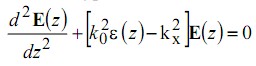
Это уравнение является уравнением Хилла, общее решение которого согласно теории Флоке-Ляпунова есть суперпозиция волн Флоке-Блоха:
E(z) = C1E1(z)+ C2E2(z), E1,2 (z) = F1,2 (z)exp(is); F1,2 (z) = F1,2 (z + d ) , S1,2 -
характеристические показатели решения. Для нахождения точных аналитических выражений для волн E 1,2 (z) , представим их в слоях с ε1, ε2 первого периода в виде:
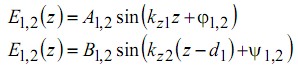
где ![]() Фазы φ1,2 и ψ1,2 в общем случае комплексные и их введение отличает используемый метод от классического способа решения данной задачи, путем представления поля в виде суперпозиции экспонент с неопределенными коэффициентами. Используя граничные условия в плоскостях z=0, z=d1 и теорему Флоке для периодических коэффициентов решения, сдвинутых на период, E1(z)=exp(is1)E1(z-d), получена система, определяющую параметры φ1, ψ1, А1,B1 волны Флоке-Блоха. Дисперсионное уравнение имеет вид:
Фазы φ1,2 и ψ1,2 в общем случае комплексные и их введение отличает используемый метод от классического способа решения данной задачи, путем представления поля в виде суперпозиции экспонент с неопределенными коэффициентами. Используя граничные условия в плоскостях z=0, z=d1 и теорему Флоке для периодических коэффициентов решения, сдвинутых на период, E1(z)=exp(is1)E1(z-d), получена система, определяющую параметры φ1, ψ1, А1,B1 волны Флоке-Блоха. Дисперсионное уравнение имеет вид:
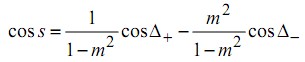
Параметры (частота, уровень сигнала и др.) периодической структуры, необходимые для обеспечения режима пропускания определяются из соотношения: cos s<1. Теорема Флоке позволяет записать искомое поле в N-ом слое:
Полное электрическое поле в областях z < 0 и как z > Nd
Учет граничных условий непрерывности поля на границах разделов сред позволяет получить аналитические соотношения для расчета коэффициентов отражения и прохождения:
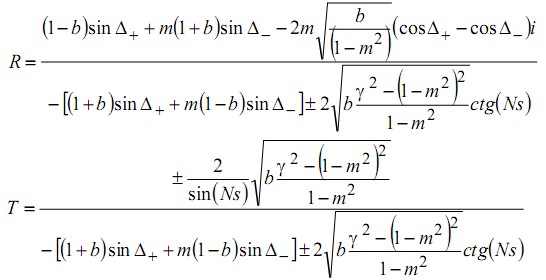
где 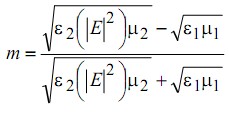 характеризует глубину оптической модуляции двухслойной периодической структуры,
характеризует глубину оптической модуляции двухслойной периодической структуры, 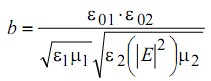 - взаимодействие электромагнитной волны с границами структуры, параметр
- взаимодействие электромагнитной волны с границами структуры, параметр 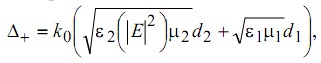 - усредненный по периоду волновой вектор света внутри структуры,
- усредненный по периоду волновой вектор света внутри структуры, 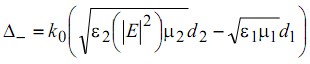 - оптическая разность фаз электромагнитных волн в базовых слоях структуры, N - число периодов.
- оптическая разность фаз электромагнитных волн в базовых слоях структуры, N - число периодов.
В запрещенных зонах коэффициент отражения R(Δ+ ) близок к единице. В разрешенных зонах его зависимость является осциллирующей с амплитудой, увеличивающейся при приближении к границам с запрещенными зонами. При D- =0 присутствуют только нечетные запрещенные зоны, т.е. зоны с центрами при Δ+ = (2n +1 ) Π , где n = 0,1,2... . При значении параметра ![]() ширины четных и нечетных запрещенных зон сравниваются, а при Δ- =Π нечетные запрещенные зоны исчезают совсем, в то время как ширины четных достигают своего максимума. Увеличение параметра b в разрешенных зонах увеличивает амплитуду осцилляции. В запрещенных зонах характер зависимости практически не меняется. При малом значении параметра m ширина разрешенных зон увеличивается, а коэффициент отражения в них стремится к нулю. При любой значении параметра модуляции m коэффициент отражения может достигать единицы при достаточно большом числе периодов. Изменение уровня сигнала Е приводит к перестройке частотных характеристик, в частности, сдвигу полос пропускания. Указанное свойство открывает возможность использования двухслойной диэлектрической периодической структуры в качестве структуры, управляемой уровнем сигнала, на основе которой возможно создание большого числа управляемых устройств.
ширины четных и нечетных запрещенных зон сравниваются, а при Δ- =Π нечетные запрещенные зоны исчезают совсем, в то время как ширины четных достигают своего максимума. Увеличение параметра b в разрешенных зонах увеличивает амплитуду осцилляции. В запрещенных зонах характер зависимости практически не меняется. При малом значении параметра m ширина разрешенных зон увеличивается, а коэффициент отражения в них стремится к нулю. При любой значении параметра модуляции m коэффициент отражения может достигать единицы при достаточно большом числе периодов. Изменение уровня сигнала Е приводит к перестройке частотных характеристик, в частности, сдвигу полос пропускания. Указанное свойство открывает возможность использования двухслойной диэлектрической периодической структуры в качестве структуры, управляемой уровнем сигнала, на основе которой возможно создание большого числа управляемых устройств.



