Обеспечение устойчивого и сбалансированного социально-экономического развития регионов является важнейшей социально значимой задачей современного прогрессивного общества, решение которой требует всестороннего исследования и мониторинга огромного числа социально-экономических показателей, что позволит определить наиболее проблемные места социально-экономической жизни граждан и факторы, способствующие повышению или понижению общего качественного восприятия условий жизнедеятельности.
Как показали исследования авторов [2,7], при оценке социально-экономического положения граждан существует необходимость единовременного учета показателей различной природы, одни из которых описывают множество изменяющихся во времени статистических характеристик, измеряемых с помощью инструментальных средств, а другие – динамическое множество субъективных показателей, анализ которых требует привлечения методов экспертного оценивания. Оценка качественных и количественных показателей осуществляется методами статистического и экономического анализа, эконометрики, социологических исследований, построением рейтинговых шкал на основе экспертных оценок. Однако не во всех случаях указанные методы способны измерить и свести воедино разнородные показатели, составленные из многоуровневых нечетких описаний и сопоставить усредненные данные, полученные из статистических сборников с личными представлениями населения о достойном, полноценном и удовлетворяющем его требованиям уровне жизни. При этом важно учитывать возможность изменения оценок по первичным признакам во времени, совокупность которых характеризует социально-экономическое положение как целостную величину.
Перечисленные обстоятельства, в целом, обусловливают очевидную необходимость разработки и применения методов и методик адекватной оценки социально-экономических показателей на основе синтеза статистических, социологических, экономико-математических и экспертных методов.
Для реализации данной задачи необходим программный инструментарий, относящийся к категории Систем поддержки принятия решений (СППР) и позволяющий реализовывать следующие функции: сбор необходимой информации из различных источников данных; поиск, преобразование, обработку и визуализацию информации в удобном для анализа и принятия решений виде; создание динамических нечетких моделей; настройку параметров моделей; сбор, обработку и хранение экспертных суждений; ведение архива решенных задач; администрирование системы, в т.ч управление правами доступа, восстановление и т.д.
Современные СППР являются результатом мультидисциплинарного исследования, основанного на теориях: баз данных, баз знаний, искусственного интеллекта, интерактивных компьютерных систем, методов имитационного моделирования и др.
Принято различать системы по управляемым ими объектам [8]. В качестве таких объектов выступают: сообщения, данные, документы, знания и модели. Разрабатываемая нами система, хотя в ней и предусмотрен анализ данных и использование базы знаний, предназначена, в первую очередь, для манипуляции математическими моделями и организации доступа к ним. Поэтому подробнее остановимся на вопросах построения используемых в системе динамических нечетких моделей.
При описании экспертами таких терминов как «благополучие», «качество и уровень жизни», «удовлетворенность» могут отсутствовать точные числовые данные, однако оценку можно сформулировать словами, такими как «низкое-высокое, удовлетворительное-неудовлетворительное». В этом случае, мы сталкиваемся с нечеткими выражениями. Для обработки нечеткой информации о качественных и количественных параметрах сложных объектов предлагается использовать математический аппарат динамических нечетких множеств [7].
С практической точки зрения каждое динамическое нечеткое множество характеризует динамическое свойство объекта сложной системы. При этом в разные моменты времени степень проявления данного свойства в системе будет непостоянной. Для того чтобы её измерить необходимо установить интервал значений от «0» до «1», где число 1 будет соответствовать абсолютному проявлению указанного свойства, а число 0 - его отсутствию. Промежуточные числа будут характеризовать систему следующим образом: чем ближе число к 1, тем сильнее обладание объектом рассматриваемым свойством, и наоборот, чем в меньшей степени рассматриваемое свойство проявляется у объекта, тем ближе к 0 должно быть значение динамического нечеткого множества. И речь идет не только том, что во времени изменяется полнота обладания данным свойством. Само по себе свойство также может изменяться. Тот набор описаний, которым характеризовался рассматриваемый объект несколько лет назад, претерпевает большие изменения на текущую дату, хотя наименование свойства будет оставаться прежним. Подобные изменения наблюдаются при изучении понятий «престижный автомобиль», «высокая скорость обработки информации», «здоровый образ жизни» и т.д.
Рассмотрим пример динамического нечеткого описания показателя «продолжительность жизни». Для этого определим нечеткое множество «Ожидаемая продолжительность жизни населения на территории» и на основе экспертных данных построим функцию принадлежности за три периода времени. Как показывает рисунок 1,а, суждения экспертов относительно ожидаемой продолжительность жизни изменялись по мере развития системы здравоохранения, роста расходов государства на охрану здоровья и борьбу с вредными привычками населения. В 1900 – е гг. продолжительность жизни составляла 31 год - у мужчин и 33 года - у женщин, о чем свидетельствует значение функции принадлежности
. Начиная со значения возраста - 32 года, принадлежность к понятию «Ожидаемая продолжительность жизни» постепенно снижается, а со значения возраста - от 45 лет и старше приравнивается к нулю. По оценкам экспертов максимальный возраст, соответствующий абсолютной принадлежности нечеткому множеству «Ожидаемая продолжительность жизни» за 2011 год составляет 68 лет, свыше этого возраста эксперты высказывают расплывчатое мнение: по мере увеличения числа лет по оси 
, значения функции принадлежности убывают. Если представить данные рисунка 1, а в трехмерной системе координат, мы получим динамическое нечеткое множество (ДНМ), графически представленное динамической функцией принадлежности (рис.1,б).
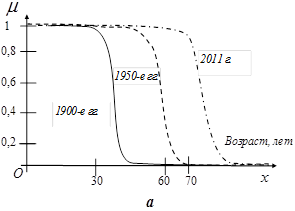
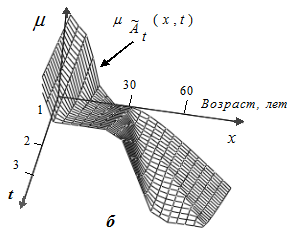
Рис.1. Функции принадлежности нечеткому множеству «Ожидаемая продолжительность жизни»
Динамика оценок обусловлена двумя группами причин:
1) Объективные причины cвязаны, прежде всего, с изменчивостью самих изучаемых объектов или явлений, а также непостоянством среды, в условиях которой они рассматриваются. Одним из примеров здесь может выступить изменение отношения экспертов к скорости обработки информации в связи с научно-техническим прогрессом, изменение запросов потребителей в связи с появлением новых товаров и услуг и т.п.;
2) Субъективные причины обусловлены изменениями внутренних суждений экспертов (ЛПР) по истечению времени, особенностей восприятия экспертами анализируемых объектов и условий среды, в которых они находятся. В данном случае изменения могут наблюдаться в отношении к таким понятиям, как «высокооплачиваемая работа», «престижный район», «хороший отдых» и т.д.
Динамическое нечеткое множество характеризуется своей функцией принадлежности, которую будем называть динамической. Любая точка, принадлежащая графику функции, будет определяться координатами: по оси абсцисс – период времени, по оси ординат – степень принадлежности, по оси аппликат – область определения нечеткого значения.
Динамическая функция принадлежности строится в несколько этапов:
1. Указание реперных и бифуркационных точек на всем горизонте построения модели. Реперная точка представляет собой точку, в которой состояние системы зафиксировано и возможно точно измерить её базовые показатели, т.к. в ближайшей от нее окрестности не происходит перелома тренда. В состоянии неустойчивости системы, когда созданы условия для резкого изменения пути её развития, возникают точки бифуркации, а точки желаемого состояния, к которому движется система, представляются точками в конечный момент времени;
2. Формирование массивов экспериментальных данных из указанных экспертом точек, описывающих степень принадлежности каждого исследуемого параметра заданному нечеткому множеству в разные моменты времени;
3. Поиск неизвестных точек путем применения алгоритмов аппроксимации;
4. Описание ДНМ и их графическое представление в виде ДФП;
5. Построение динамического терм-множества значений показателей.
Графически исходное положение дел проиллюстрировано на рисунке 2,а, на котором отражены точки, разбросанные в координатном пространстве экономического объекта. Указанные экспертом точки формируются в массивы экспериментальных данных, описывающих степень принадлежности каждого исследуемого параметра заданному нечеткому множеству в разные моменты времени. Для построения трехмерного графика динамического нечеткого множества необходимо найти все недостающие точки. Такая задача достаточно удовлетворительно решается с помощью существующих алгоритмов аппроксимации. В результате решения задач интерполяции и подбора зависимостей, все недостающие точки будут найдены (рис.2,б), будет получен числовой ряд, наиболее точно определяющий функцию принадлежности каждого показателя.
Рис.2. Построение динамической функции принадлежности по базовым точкам
Интерактивный процесс экспертного оценивания свойств сложных систем, визуализированных с помощью динамических функций, обеспечивается за счет уже созданных программных систем [3,4].
Разработанная архитектура интеллектуальной системы поддержки принятия решений (рис. 3) основывается на стандартных схемах построения СППР [5,6], дополненных рядом модулей, предназначенных для решения поставленной задачи.
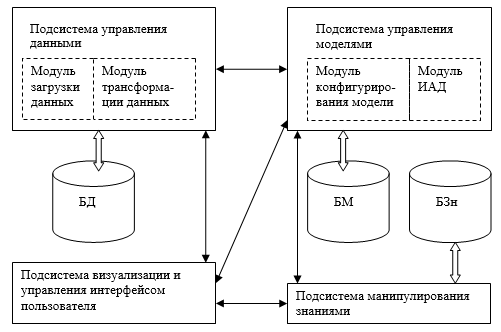
Рис. 3. Архитектура интеллектуальной системы поддержки принятия решений.
Подсистема управления данными, помимо стандартных средств манипулирования данными, реализуемых в СУБД, должна выполнять следующие функции:
- загрузку данных по социально-экономическим показателям из различных источников информации, в качестве которых выступают статистические органы, а также результатов субъективной оценки населения своего уровня жизни;
- трансформацию данных для их последующей обработки математическими моделями и методами интеллектуального анализа данных.
Учитывая то, что и показатели, и субъективные оценки представлены в динамике, мы имеем многомерный характер данных. БД строится на основе одной из разновидностей многомерной модели – ROLAP, использующей реляционные принципы. Схема структуры каждого из кубов имеет тип «звезда» с одной фактографической таблицей, в которой и хранятся данные, и несколькими справочными, каждая из которых характеризует одну из граней куба. В качестве примера рассмотрим инфологическую модель для фрагмента БД, хранящего информацию о социально-экономических показателях (рис. 4).
Подсистема манипулирования знаниями предназначена для организации хранения, редактирования и выдачи по запросу из подсистемы управления моделями экспертных знаний о конфигурациях моделей; организации ввода, хранения, редактирования и выдачи по запросу из подсистемы управления моделями нечетких продукционных правил.
Исходя из этих функций, База знаний имеет две структурно различные части:
1. База параметров моделей, организованная по принципам реляционной Базы данных.
2.База правил, представленная в виде совокупности причинно-следственных отношений.
Рис. 4. Фрагмент БД по социально-экономическим показателям.
Подсистема управления моделями, помимо стандартных функций создания и манипулирования математическими моделями, должна выполнять поиск зависимостей между различными социально-экономическими показателями и субъективными оценками, используя методы статистического, эконометрического и интеллектуального анализа данных; конфигурирование математических моделей на основе архива ранее решаемых задач.
Подсистема визуализации и управления интерфейсом пользователя должна обеспечивать дружественный интерфейс и, учитывая многомерный характер анализируемых данных, широкий набор средств визуализации выходной информации, в т.ч. 3D-графику.
Динамические нечеткие модели предоставляют совершенно новые уникальные возможности по совершенствованию и оптимизации всей процедуры аккумуляции знаний эксперта и извлечения недостающих значений принадлежностей элементов параметров нечетким множествам на всем диапазоне экспертного оценивания. Теоретико-методологические положения и инструментальные средства, предложенные авторами, позволяют анализировать сложную структуру социально-экономических показателей, характеризующих отдельные составляющие условий жизнедеятельности населения, с учетом динамики их изменения под воздействием объективных и субъективных факторов.
Исследование выполнено при финансовой поддержке РГНФ в проекте проведения научных исследований «Динамическое нечеткое моделирование социально-экономических показателей региона», проект № 14-12-34010
Рецензенты:
Рогачев А.Ф., д.т.н., профессор, заведующий кафедрой «Математическое моделирование и информатика», Волгоградский государственный аграрный университет, г. Волгоград;
Терелянский П.В., д.э.н., доцент, заведующий кафедрой «Информационные системы в экономике», Волгоградский государственный технический университет, г. Волгоград.