55-летию Российского университета
дружбы народов посвящается
Задача идентификационного управления [1] возникает в тех случаях, когда модель объекта управления неизвестна или очень сложна и математический вывод модели требует существенных затрат. Часто такая ситуация возникает при построении моделей многозвенных роботов, когда большое количество степеней свободы приводит к модели большой размерности. В некоторых случаях задача управления не требует использования всех уравнений моделей объекта, достаточно ограничиться упрощенной моделью или выполнить декомпозицию системы уравнений.
В настоящей работе мы решаем задачу идентификационного управления численным методом сетевого оператора [2-7]. Метод позволяет находить с помощью эволюционного алгоритма структуры и параметры математических выражений в виде целочисленной матрицы. Первоначально мы применяем метод сетевого оператора для решения задачи идентификации, где в качестве критерия используем норму отклонения траектории объекта от экспериментальных данных. Эксперимент выполняем на реальном объекте, применяя управление близкое к требуемой задаче синтеза. На втором этапе решаем задачу синтеза системы оптимального управления также методом сетевого оператора. Используем другой сетевой оператор, другой размерности и с другими критериями качества. Полученный в результате синтеза сетевой оператор реализуем в блоке управления реального объекта и с помощью моделирования проверяем результаты решения задачи синтеза идентификационного управления.
1. Задача идентификации математической модели объекта управления
Заданы размерность ![]() модели объекта управления и размерность
модели объекта управления и размерность ![]() вектора управления.
вектора управления.
Заданы экспериметальные данные в виде упорядоченного набора числовых данных
![]() , (1)
, (1)
где ![]() ,
, ![]() ,
, ![]() .
.
Необходимо найти модель в форме
![]() , (2)
, (2)
где ![]() – искомые математические выражения.
– искомые математические выражения.
Решение системы уравнений (2)
![]() ,
,
где ![]() при
при ![]() , должно обеспечить минимум следующих критериев:
, должно обеспечить минимум следующих критериев:
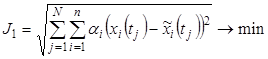 , (3)
, (3)
![]() , (4)
, (4)
где ![]() – заданные весовые коэффициенты.
– заданные весовые коэффициенты.
Данная задача относится к классу задач структурно-параметрической многокритериальной оптимизации. Решением задачи является множество Парето на пространстве критериев (3), (4).
2. Задача синтеза управления
Задана математическая модель объекта управления в виде (2). Задана область начальных условий
![]() . (5)
. (5)
Заданы ограничения на управление
![]() . (6)
. (6)
Заданы терминальные условия
![]() .
. ![]() . (7)
. (7)
Задан критерий качества, который показывает точность отклонения от траектории
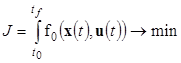 . (8)
. (8)
Необходимо найти управление в виде
![]() , где
, где ![]() .
.
Функция ![]() обеспечивает удовлетворение ограничений на управление (6) и для любого решения дифференциального уравнения
обеспечивает удовлетворение ограничений на управление (6) и для любого решения дифференциального уравнения
![]()
с начальными условиями ![]() достижение терминальных условий (7) и минимальное значение функционала (8).
достижение терминальных условий (7) и минимальное значение функционала (8).
Для решения задач идентификации математической модели объекта управления и синтеза управления в работе используем метод сетевого оператора.
3. Вычислительный эксперимент
В качестве вычислительного эксперимента было рассмотрено решение задачи синтеза идентификационного управления для одного эталонного объекта управления [12] (рис. 1).
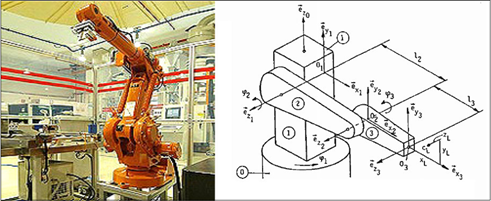
Рис. 1. Робот-манипулятор.
Математическая модель робота, изображенного на рис. 1 представлена в работе [12]. Мы предполагали, что не знаем эту модель, а располагаем самим техническим объектом, на котором можем проводить эксперименты. Нам известно, что вектором управления являются электромагнитные моменты ![]() , которые действуют на ротор
, которые действуют на ротор ![]() двигателя. Компонентами вектора состояния являются углы вращения в местах соединения
двигателя. Компонентами вектора состояния являются углы вращения в местах соединения ![]()
![]() .
.
В эксперименте для получения исходных данных управление роботом осуществлялось с помощью тестовых функций времени
![]() ,
,
![]() ,
,
![]() .
.
Был проведен ряд экспериментов и были получены значения переменных в 21-й точке. Экспериментальные данные приведены в табл. 1 .
Таблица 1
Экспериментальные данные
|
|
t |
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
0 |
-0.55 |
-0.0054 |
0.4 |
|
2 |
0.1 |
0 |
0 |
-0.032 |
-0.053 |
0.3674 |
0.001 |
|
3 |
0.2 |
0 |
-0.02 |
-0.1025 |
-0.0487 |
0.2768 |
-0.005 |
|
4 |
0.3 |
0 |
-0.049 |
-0.2505 |
-0.04175 |
0.2897 |
-0.001 |
|
5 |
0.4 |
-0.007 |
-0.084 |
-0.4111 |
-0.0303 |
-0.3294 |
-0.003 |
|
6 |
0.5 |
-0.01 |
-0.1463 |
-0.6418 |
-0.01882 |
-0.3209 |
-0.0045 |
|
7 |
0.6 |
-0.02 |
-0.2212 |
-0.8503 |
-0.0013 |
-0.3098 |
-0.6859 |
|
8 |
0.7 |
-0.04827 |
-0.35 |
-1.042 |
-0.473 |
-0.2998 |
-0.093 |
|
9 |
0.8 |
-0.07 |
-0.4684 |
-1.223 |
-0.455 |
-0.2912 |
-0.117 |
|
10 |
0.9 |
-0.1162 |
-0.6405 |
-1.319 |
-0.4288 |
-0.2818 |
0.6481 |
|
11 |
1 |
-0.1654 |
-0.7917 |
-1.323 |
-0.4064 |
-0.2715 |
0.6112 |
|
12 |
1.1 |
-0.2462 |
-0.9772 |
-1.247 |
-0.3819 |
-0.2632 |
0.5796 |
|
13 |
1.2 |
-0.3132 |
-1.093 |
-1.085 |
-0.3547 |
-0.2548 |
0.5433 |
|
14 |
1.3 |
-0.4399 |
-1.216 |
-0.8576 |
-0.3272 |
-0.2472 |
0.5066 |
|
15 |
1.4 |
-0.5139 |
-1.32 |
-0.5798 |
-0.2933 |
-0.2398 |
0.4614 |
|
16 |
1.5 |
-0.6424 |
-1.407 |
-0.2505 |
-0.2656 |
-0.233 |
0.4244 |
|
17 |
1.6 |
-0.7539 |
-1.452 |
0.007 |
-0.2337 |
0.3979 |
0.382 |
|
18 |
1.7 |
-0.8863 |
-1.463 |
0.2505 |
-0.2082 |
0.4029 |
0.348 |
|
19 |
1.8 |
-1.01 |
-1.431 |
0.3952 |
-0.1779 |
0.4077 |
0.3075 |
|
20 |
1.9 |
-1.177 |
-1.353 |
0.4444 |
-0.1507 |
0.4098 |
-0.5227 |
|
21 |
2 |
-1.288 |
-1.23 |
0.373 |
-0.1202 |
0.4119 |
-0.5635 |
При решении задачи идентификации методом сетевого оператора было выбрано следующее базисное решение
![]() ,
,
![]() ,
,
![]() .
.
Выбор данного базисного решения соответствует линейной модели объекта управления.
Базисные значения параметров: ![]()
Параметры генетического алгоритма: размерность популяции – 256, количество скрещиваемых пар в поколении – 64, количество поколений – 256, число поколений между эпохами – 20, длина структурной части хромосомы – 8, число постоянных параметров – 6, количество бит под целую часть параметра – 2, количество бит под дробную часть параметра – 6, вероятность мутации – 0,7, шаг интегрирования – 0.001, размерность матрицы сетевого оператора – 24 х 24. Расчет проводился на программном комплексе NOP4C-I для идентификации систем управления методом сетевого оператора, разработанном на кафедре кибернетики и мехатроники РУДН [8]. Время расчета составляло 2,2 часа на ЭВМ с частотой процессора 2,2 ГГц, тип процессора Intel Core i5.
В результате была получена следующая матрица сетевого оператора:

В матрице сетевого оператора номера унарных и бинарных операций соответствуют функциям, приведенным в приложениях [3]. В результате по матрице сетевого оператора получаем следующее решение:
![]() , (9)
, (9)
![]() , (10)
, (10)
![]()
![]()
![]() , (11)
, (11)
где ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
Результаты моделирования полученной модели системы управления представлены на рис. 2-4. Кружками отмечены экспериментальные данные из таблицы 1.
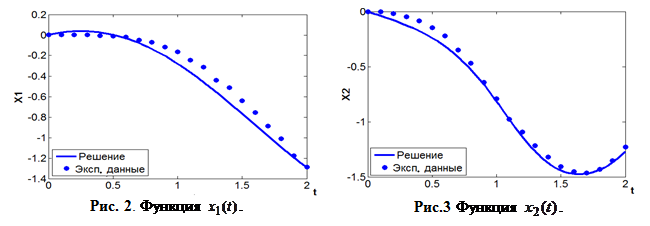
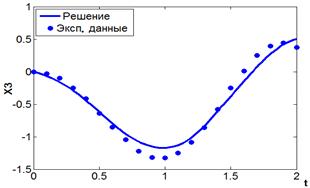
Рис. 4. Функция ![]() .
.
Как видно из графиков, решение, полученное в результате идентификации математической модели, достаточно хорошо соответствуют результатам экспериментов.
На втором этапе для проверки правильности решения задачи идентификации решаем задачу синтеза управления по полученной на этапе идентификации модели. Для решения задачи синтеза также применяем метод сетевого оператора.
В качестве цели управления задаем траекторию, которую необходимо пройти от точки к точке (см. рис. 5-7).
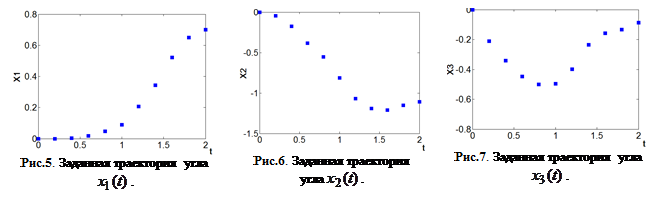
Критериями качества управления считаем нормы отклонения от заданной траектории, аналогичные соотношениям (3), (4).
Выбираем базисное решение в виде:
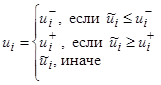 ,
, ![]() ,
,
где
![]() ,
,
![]() ,
,
![]() .
.
Базисные значения параметров: ![]()
Ограничения на управление имели следующие значения ![]() ,
, ![]() ,
, ![]() .
.
При решении использовали следующие параметры генетического алгоритма: размерность популяции – 256, количество скрещиваемых пар в поколении – 64, количество поколений – 256, число поколений между эпохами – 30, длина структурной части хромосомы – 8, число постоянных параметров – 6, количество бит под целую часть параметра – 4, количество бит под дробную часть параметра – 4, вероятность мутации – 0,7, шаг интегрирования – 0.001, размерность матрицы сетевого оператора – 16х16. Расчет проводился на программном комплексе NOP4C-S для идентификации систем управления методом сетевого оператора, разработанном на кафедре кибернетики и мехатроники РУДН [9]. Время расчета составляло 2 часа на ЭВМ с частотой процессора 2,2 ГГц, тип процессора Intel Core i5.
В результате была получена следующая матрица сетевого оператора:
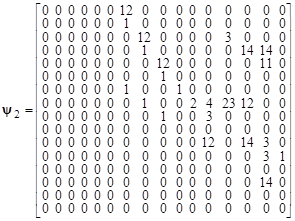 .
.
Данная матрица соответствует следующим математическим выражениям:
![]() ,
,
![]()
![]() ,
,
![]() .
.
где ![]()
Графики управления представлены на рис. 8-10.
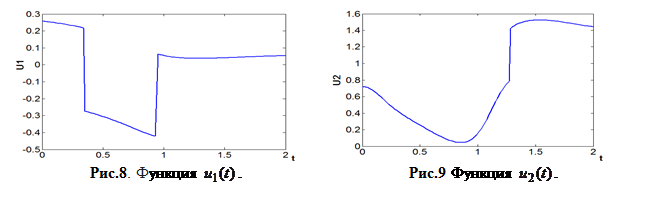
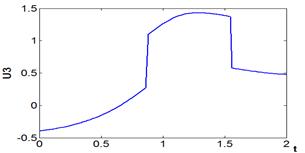
Рис.10. Функция ![]() .
.
На рис. 11-13 приведены результаты моделирования полученной системы управления.
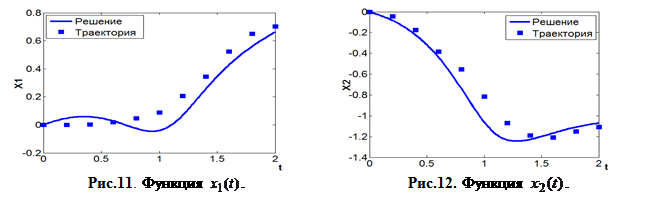
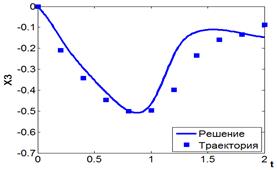
Рис.13. Функция ![]() .
.
Для сравнения на рис. 11-13 приведены траектории движения робота, полученные с помощью идентифицированной и реальной моделей. Как видно из графиков, полученная при идентификации математическая модель позволяет синтезировать систему управления роботом, которая обеспечивает движение реального объекта по заданной траектории.
Рассмотрим решение задачи синтеза системы управления для разных начальных значений. Задаем для системы (9)-(11) множество начальных значений
![]() . (12)
. (12)
Задаем траекторию (см. рис. 5-7). В качестве критериев отбора оптимальных решений используем суммы значений критериев, вычисленных для каждого начального состояния.
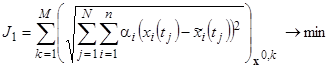 , (13)
, (13)
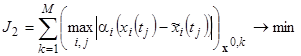 . (14)
. (14)
В результате синтеза системы управления методом сетевого оператора была получена следующая матрица сетевого оператора:
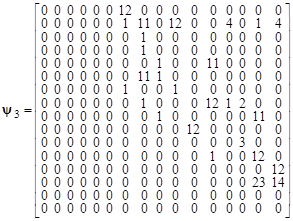 .
.
Данная матрица соответствует следующим математическим выражениям
![]() ,
,
![]()
![]() ,
,
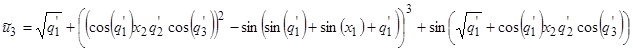 ,
, ![]() .
.
Графики изменения управления представлены на рис. 14-16.
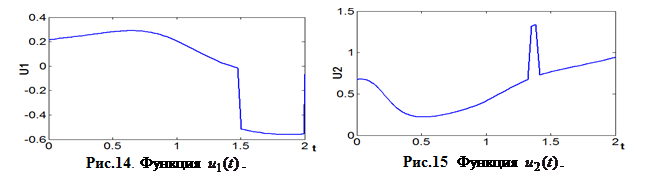
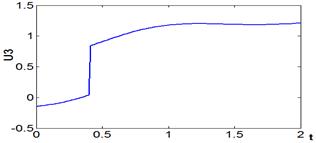
Рис.16. Функция ![]() .
.
На рис. 17-19 приведены результаты моделирования полученной системы управления с разными начальными значениями. Красный цвет соответствует результатам моделирования с начальными значениями ![]() , зеленый цвет –
, зеленый цвет – ![]() , синий цвет –
, синий цвет – ![]() .
.
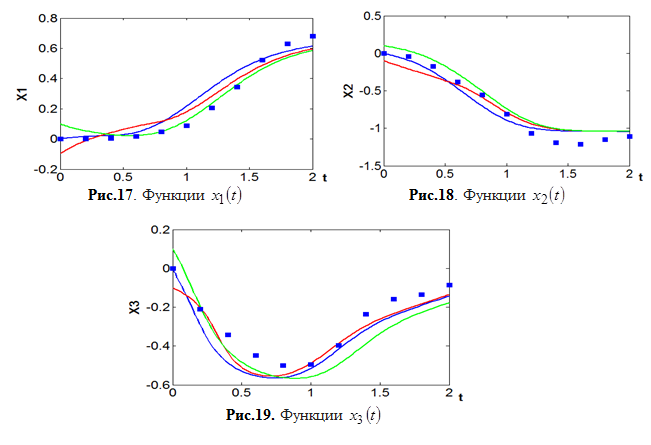
Как видно из графиков, полученная при идентификации математическая модель позволяет синтезировать систему управления роботом-манипулятором, которая обеспечивает движение реального объекта по заданной траектории при различных начальных значениях.
Заключение
В результате применения метода сетевого оператора была решена задача синтеза идентификационного управления. Результаты вычислительных экспериментов с эталонной моделью робота показали удовлетворительное качество решения задач идентификации и синтеза системы управления.
Работа выполнена по темам грантов РФФИ №13-08-00523-а «Исследование и разработка численного метода идентификации моделей интеллектуальных систем управления», № 14-08-00008-а «Исследование методов синтеза систем управления в условиях неопределенности».
Рецензенты:
Никульчев Е.В., д.т.н., профессор, Негосударственное образовательное учреждение ВПО, Московский технологический институт, г. Москва.
Юрков Н.К., д.т.н., профессор, ФГБОУ ВПО «Пензенский государственный университет», г. Пенза.



