Абсорбция газов сопровождается тепловыми эффектами, которые, как правило, оказывают влияние на процесс массообмена [8,9]. В работах [5.6] приводится основы разработанной в рамках нелокальной версии термодинамики [3,4] кинетической модели расчета многокомпонентной неизотермической абсорбции. Эта модель включает:
-
уравнение массопередачи для неизотермических условий
![]() , (1)
, (1)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() - константа фазового равновесия для i-го компонента;
- константа фазового равновесия для i-го компонента;
![]() - коэффициент массопередачи i-го компонента,
- коэффициент массопередачи i-го компонента, ![]() ;
;
![]() - коэффициенты массоотдачи,
- коэффициенты массоотдачи, ![]() ,
,
![]() - член уравнения массопередачи, учитывающий термодиффузию компонента через границу раздела фаз, имеет размерность концентрации (мольные доли).
- член уравнения массопередачи, учитывающий термодиффузию компонента через границу раздела фаз, имеет размерность концентрации (мольные доли).
-
уравнение теплопередачи (с учетом тепловых эффектов на границе раздела фаз)
![]() (2)
(2)
-
уравнение для расчета равновесной температуры на границе раздела фаз
![]() , (3)
, (3)
здесь ![]() - коэффициенты теплоотдачи в газовой и жидкой фазах соответственно,
- коэффициенты теплоотдачи в газовой и жидкой фазах соответственно, ![]() ;
;
![]() - теплота абсорбции,
- теплота абсорбции, ![]() ;
;
![]() - теплота испарения растворителя,
- теплота испарения растворителя, ![]() ;
;
![]() - температуры в ядре потока газовой и жидкой фаз соответственно, K.
- температуры в ядре потока газовой и жидкой фаз соответственно, K.
При разработке модели принималось, что перенос массы и тепла происходит в тонком пограничном слое, прилегающем к границе раздела фаз, по линейному закону[1,7]. Величины ![]() , входящие в уравнение для коэффициентов массоотдачи, а также величины
, входящие в уравнение для коэффициентов массоотдачи, а также величины ![]() (
(![]() ), входящие в уравнение для коэффициентов теплоотдачи, рассчитываются теоретически. Они зависят от физических свойств смеси - скорости звука
), входящие в уравнение для коэффициентов теплоотдачи, рассчитываются теоретически. Они зависят от физических свойств смеси - скорости звука ![]() , плотности
, плотности ![]() , молекулярной массы
, молекулярной массы ![]() . Безразмерный коэффициент переноса субстанции
. Безразмерный коэффициент переноса субстанции ![]() характеризует гидродинамические условия, в которых протекают процессы тепло- и массопередачи и теоретически не может быть определен в рамках поставленной в статье задачи. В общем случае коэффициент переноса
характеризует гидродинамические условия, в которых протекают процессы тепло- и массопередачи и теоретически не может быть определен в рамках поставленной в статье задачи. В общем случае коэффициент переноса ![]() меньше единицы. В пределе он может быть равным единице и тогда
меньше единицы. В пределе он может быть равным единице и тогда ![]() , а
, а ![]() , то есть процесс переноса массы и тепла будет происходить с максимально возможной скоростью, равной скорости звука в данной среде, а толщина пограничного ламинарного слоя
, то есть процесс переноса массы и тепла будет происходить с максимально возможной скоростью, равной скорости звука в данной среде, а толщина пограничного ламинарного слоя![]() будет равна характерному линейному размеру
будет равна характерному линейному размеру ![]() .
.
При использовании уравнения массопередачи (1) и уравнения теплопередачи (2) для расчета тепломассообменного процесса коэффициентами переноса ![]() и
и ![]() необходимо задаваться и корректировать их в зависимости от того, какое распределение концентраций по высоте аппарата необходимо получить. Поэтому задача расчета неизотермического абсорбера ставится в поверочном варианте.
необходимо задаваться и корректировать их в зависимости от того, какое распределение концентраций по высоте аппарата необходимо получить. Поэтому задача расчета неизотермического абсорбера ставится в поверочном варианте.
Расчет процесса переноса тепла и массы, которые происходят в реальном массообменном аппарате, на основе уравнений (1), (2) и (3) сводится к процедуре численного интегрирования. При составлении алгоритма и программы расчета неизотермического абсорбера в качестве метода сходимости был использован метод простых итераций. Предварительно рабочая часть аппарата разбивается на заданное число элементарных объемов. Затем колонна «заполняется» газом, равным по количеству и составу сырому газу. Следующий этап – это последовательный расчет аппарата сверху вниз. При этом каждый ![]() й элементарный объем массообменного аппарата рассчитывается следующим образом.
й элементарный объем массообменного аппарата рассчитывается следующим образом.
1. Предварительно задается температура на границе раздела фаз ![]() равной температуре жидкости
равной температуре жидкости ![]() . По этой температуре выбираются константы фазового равновесия
. По этой температуре выбираются константы фазового равновесия ![]() . Затем по уравнению (1) рассчитываются удельные мольные потоки компонентов.
. Затем по уравнению (1) рассчитываются удельные мольные потоки компонентов.
2. Истинное изменение мольного количества распределяющихся компонентов в газовой фазе ![]() в элементе колонного аппарата высотой
в элементе колонного аппарата высотой ![]() определяется с помощью уравнения материального баланса, записанного в конечно-разностной форме
определяется с помощью уравнения материального баланса, записанного в конечно-разностной форме
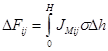 , (4)
, (4)
где ![]() - поверхность контакта в единице объема,
- поверхность контакта в единице объема, ![]() ,
,
![]() – рабочая высота аппарата,
– рабочая высота аппарата, ![]() .
.
3. По формуле (3) уточняется значение температуры на границе раздела фаз ![]() до тех пор пока разность значений
до тех пор пока разность значений ![]() на двух соседних итерациях не будет удовлетворять заранее заданной точности расчета. Таким образом, из формулы (3) итерационным путем находим
на двух соседних итерациях не будет удовлетворять заранее заданной точности расчета. Таким образом, из формулы (3) итерационным путем находим ![]() , а из уравнения (4)
, а из уравнения (4) ![]() .
.
4. Суммируя покомпонентные изменения газовой фазы, определяем общее изменение расхода газа
![]() .
.
5. По уравнению материального баланса определяются искомые параметры выходных потоков ![]() -го элемента аппарата
-го элемента аппарата
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
6. По уравнению (2) определяются удельные количества теплоты в обеих фазах.
7. Истинные изменения количества теплоты в газовой и жидкой фазах определяются из уравнений
![]() ,
,
![]() .
.
8. Температуры потоков, покидающих элементарный объем аппарата, определяются из уравнений теплового баланса
![]()
![]()
![]()
![]()
где ![]() - молярная газовая теплоемкость,
- молярная газовая теплоемкость, ![]() ;
;
![]() - теплоемкость жидкости,
- теплоемкость жидкости, ![]() ;
;
![]() ,
, ![]() - теплосодержание соответственно газовой и жидкой фаз,
- теплосодержание соответственно газовой и жидкой фаз, ![]() .
.
Полученные в результате первого приближения выходные параметры жидкой фазы ![]() вследствие произвольного выбора газа заполнения, не будут удовлетворять уравнению покомпонентного материального баланса
вследствие произвольного выбора газа заполнения, не будут удовлетворять уравнению покомпонентного материального баланса
![]() (5)
(5)
Поэтому дальнейший расчет аппарата повторяется в направлении снизу вверх и сверху вниз до тех пор, пока не будет выполнено условие (5).
Адекватность предложенной теоретической модели расчета неизотермической абсорбции была проверена на примере системы с одним распределяющимся компонентом. В ходе экспериментального исследования изучалась абсорбция аммиака водой из аммиачно-воздушной смеси. Массообменный аппарат представлял собой пленочную колонну высотой 1,2 м и диаметром 0,0275 м. Конструкция колонны позволяла проводить промежуточные отборы проб газа и жидкости. Концентрационные профили аммиака в обеих фазах измерялись при различных гидродинамических режимах. Температуры материальных потоков измерялись на входе и выходе из аппарата. В таблице 1 приведены экспериментальные и расчетные значения концентрации аммиака в газовой и жидкой фазах при различных скоростях газа ![]() и плотности орошения
и плотности орошения ![]() .
.
Таблица 1
Экспериментальные и расчетные значения концентраций аммиака по высоте колонны
|
Скорость газа |
Экспериментальные данные |
Расчетные данные |
|
|
|||
|
|
|
|
|
||||
|
|
0,000 0,002 0,007 0,014 |
0,016 0,025 0,035 0,062 |
0,000 0,002 0,006 0,012 |
0,013 0,023 0,038 0,062 |
0,0 0,0 14,0 14,0 |
18,0 8,0 8,0 0,0 |
|
|
|
0,000 0,004 0,016 0,026 |
0,024 0,034 0,046 0,062 |
0,000 0,006 0,014 0,023 |
0,025 0,036 0,048 0,062 |
0,0 16,0 12,5 11,5 |
4,0 5,5 4,0 0,0 |
|
|
|
0,000 0,008 0,020 0,036 |
0,030 0,038 0,047 0,061 |
0,000 0,009 0,021 0,031 |
0,030 0,040 0,051 0,061 |
0,0 10,0 5,0 13,8 |
0,0 5,0 7,8 0,0 |
|
На рис.1 представлены профили изменения концентраций и температур аммиака в жидкой и газовой фазах по высоте пленочного абсорбера для скорости газа ![]() и плотности орошения
и плотности орошения ![]() . Экспериментальный температурный профиль в жидкой фазе несколько отличается от расчетного. Очевидно, это связано с тем, что пленочный абсорбер не имел тепловой изоляции, температура окружающей среды в ходе эксперимента была близка к
. Экспериментальный температурный профиль в жидкой фазе несколько отличается от расчетного. Очевидно, это связано с тем, что пленочный абсорбер не имел тепловой изоляции, температура окружающей среды в ходе эксперимента была близка к ![]() и тепловые потери отразились в первую очередь на температуре жидкой фазы. Анализ табличных данных и графического материала позволяет сделать вывод о том, кинетическая модель адекватно описывает процессы тепломассопереноса при неизотермической абсорбции.
и тепловые потери отразились в первую очередь на температуре жидкой фазы. Анализ табличных данных и графического материала позволяет сделать вывод о том, кинетическая модель адекватно описывает процессы тепломассопереноса при неизотермической абсорбции.
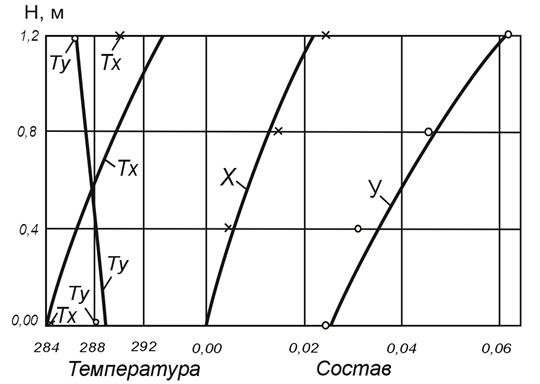
Рис. 1. Распределение концентраций температур по высоте
пленочного абсорбера в газовой (У) и жидкой (Х) фазах:
(0, ×) – экспериментальные данные; (— ) – расчетные данные.
![]()
![]() .
.
При обработке экспериментальных данных коэффициент переноса ![]() определялся на основе предположения о том, что перепад концентраций
определялся на основе предположения о том, что перепад концентраций ![]() происходит на всей толщине жидкой пленки (т.е. толщина пограничного ламинарного слоя в жидкой фазе равна толщине пленки жидкости). Коэффициент переноса в газовой фазе подбирался в ходе расчета до наилучшего совпадения экспериментальных и расчетных данных.
происходит на всей толщине жидкой пленки (т.е. толщина пограничного ламинарного слоя в жидкой фазе равна толщине пленки жидкости). Коэффициент переноса в газовой фазе подбирался в ходе расчета до наилучшего совпадения экспериментальных и расчетных данных.
Рассчитаем противоточный абсорбер для разделения многокомпонентной углеводородной смеси. В качестве абсорбента используется керосиновая фракция с молекулярным весом ![]() и плотностью
и плотностью ![]() . Количество поступающего на абсорбцию газа
. Количество поступающего на абсорбцию газа ![]() , количество тощего абсорбента
, количество тощего абсорбента ![]() , коэффициенты переноса
, коэффициенты переноса ![]() , рабочая высота аппарата
, рабочая высота аппарата ![]() , удельная поверхность контакта фаз в единице объема
, удельная поверхность контакта фаз в единице объема ![]() .
.
Экспериментальные и расчетные значения концентраций компонентов приведены в таблице 2. Экспериментальные данные заимствованы из работы [2]. Сравнение экспериментальных и расчетных значений выходных концентраций в сухом газе и насыщенном абсорбенте показывает хорошее их совпадение.
Таблица 2
Экспериментальные и расчетные значения концентраций
(многокомпонентная углеводородная смесь)
|
Компо- нент |
Сырой газ (эксп) |
Тощий абсорб. (эксп.) |
Сухой газ (эксп.) |
Сухой газ (расчет) |
Насыщ. абсоб. (экспер.) |
Насыщ. абсоб. (расчет) |
|
|
0,110 |
0,000 |
0,151 |
0,132 |
0,000 |
0,002 |
|
|
0,364 |
0,000 |
0,477 |
0,422 |
0,007 |
0,030 |
|
|
0,211 |
0,000 |
0,240 |
0,218 |
0,053 |
0,059 |
|
|
0,215 |
0,015 |
0,112 |
0,171 |
0,192 |
0,151 |
|
|
0,036 |
0,010 |
0,006 |
0,021 |
0,041 |
0,042 |
|
|
0,047 |
0,042 |
0,010 |
0,030 |
0,113 |
0,071 |
|
|
0,016 |
0,022 |
0,004 |
0,007 |
0,039 |
0,035 |
|
Абсорб. |
0,000 |
0,911 |
- |
- |
0,555 |
0,610 |
|
Тем-ра,К |
308,0 |
307,0 |
308,0 |
325,6 |
315,0 |
329,3 |
Подводя итог вышеизложенному, можно сделать вывод, что предложенный кинетический метод расчета многокомпонентной неизотермической абсорбции разработанный в рамках нелокальной версии термодинамики, позволяет раскрыть физический смысл коэффициентов массоотдачи, массопередачи, теплоотдачи, выделить гидродинамическую составляющую этих коэффициентов и поставить на повестку дня разработку теоретических методов определения коэффициентов переноса, отвечающих за гидродинамическую обстановку в зоне переноса массы и тепла через границу раздела фаз. Учет тепловых эффектов процесса абсорбции позволит в дальнейшем изучить их влияние на точность определения концентраций компонентов в газовой и жидкой фазах при изменении расходных показателей контактирующих фаз.
Рецензенты:
Богомолов А.Н., д.т.н., профессор, проректор по научной работе ФГБОУ ВПО «Волгоградский государственный архитектурно-строительный университет», г. Волгоград;
Семенов Б.А., д.т.н., профессор, заведующий кафедрой «Промышленная теплотехника» ФГБОУ ВПО «Саратовский государственный технический университет им. Ю.А. Гагарина», г. Саратов.



