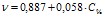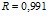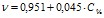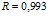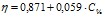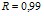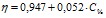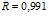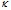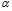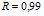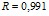Лекарственные препараты на основе белков (альбуминов, иммуноглобулинов, интерферонов) находят очень широкое применение в медицине и фармации ввиду жизненно важных функций данных белков в организме и возможности осуществлять эффективную терапию препаратами, содержащими белки. При этом к растворам для инъекций и инфузий предъявляются серьезные требования по изотоничности и изовязкости данных лекарственных форм крови человека.
В связи с этим целью данного исследования являлось изучение зависимости показателя преломления и вязкости водных растворов белков от их концентрации, а также определение границ применимости уравнения Эйнштейна для математического описания полученных функций вязкости.
Материалы и методы исследования
В качестве объекта исследования использовали растворы альбумина для инфузий и иммуноглобулина нормального с концентрацией 10%, произведенные на Челябинской станции переливания крови, а также интерферон альфа лейкоцитарный человеческий, произведенный ФГУП «НПО «МИКРОГЕН».
Вязкость растворов, термостатированных при 20 °С, определяли при помощи капиллярного вискозиметра серии ВПЖ-1 с диаметром капилляра 0,54 мм (константа капилляра 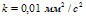 ).
).
Показатель преломления изучаемых растворов определяли при помощи портативного рефрактометра ИРФ 454Б2М.
Результаты и их обсуждение
Растворение в воде даже небольших количеств интерферона альфа лейкоцитарного человеческого или альбумина (1% или менее) приводит к достаточно резкому снижению кинематической и динамической вязкости по сравнению с дистиллированной водой. Разбавленный водный раствор, содержащий белок, более текуч, чем чистая вода. Если для дистиллированной воды экспериментально найдены значения кинематической и динамической вязкости 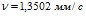 и
и 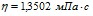 соответственно, то введение интерферона альфа лейкоцитарного человеческого уменьшает эти показатели примерно на 0,4, а введение альбумина – примерно на 0,5 (рис. 1, 2). Можно предположить, что данное уменьшение определенным образом коррелирует с молекулярной массой белка – чем выше молекулярная масса, тем больше снижение вязкости разбавленного раствора, содержащего белок, по сравнению с водой (табл. 1, рис. 1, 2).
соответственно, то введение интерферона альфа лейкоцитарного человеческого уменьшает эти показатели примерно на 0,4, а введение альбумина – примерно на 0,5 (рис. 1, 2). Можно предположить, что данное уменьшение определенным образом коррелирует с молекулярной массой белка – чем выше молекулярная масса, тем больше снижение вязкости разбавленного раствора, содержащего белок, по сравнению с водой (табл. 1, рис. 1, 2).
В дальнейшем рост концентрации белка в водном растворе (до 10%) вызывает линейное повышение кинематической и динамической вязкости (рис. 1, 2).

Рис. 1. Изменение кинематической (1) и динамической (2) вязкости водного раствора от концентрации интерферона альфа лейкоцитарного человеческого.
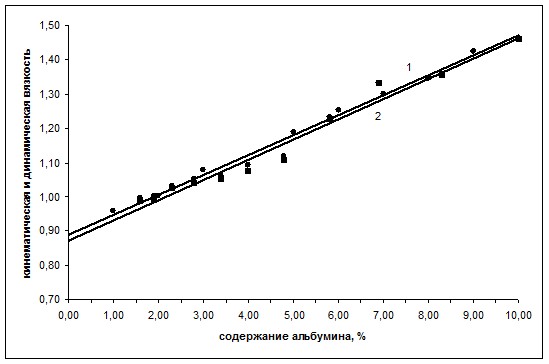
Рис. 2. Изменение кинематической (1) и динамической (2) вязкости водного раствора от концентрации альбумина.
Таблица 1
Аналитический вид зависимостей кинематической и динамической вязкости водных растворов альбумина и интерферона альфа лейкоцитарного человеческого от концентрации белка
|
Математическое описание концентрационных зависимостей вязкости |
Для водных растворов альбумина |
Для водных растворов интерферона альфа лейкоцитарного человеческого |
|
Уравнение регрессии вида |
||
|
Кинематическая вязкость |
|
|
|
Динамическая вязкость |
|
|
Из литературных данных [6; 7] известно, что линейная зависимость вязкости раствора от концентрации растворенного вещества, в случае коллоидных растворов и растворов высокомолекулярных веществ, не взаимодействующих с молекулами растворителя, описывается уравнением Эйнштейна: 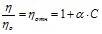 , где
, где 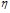 - вязкость раствора, мПа∙с;
- вязкость раствора, мПа∙с; 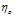 - вязкость растворителя, мПа∙с; С – объемная доля растворенного вещества;
- вязкость растворителя, мПа∙с; С – объемная доля растворенного вещества; 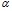 - коэффициент пропорциональности, учитывающий форму частиц в растворе (
- коэффициент пропорциональности, учитывающий форму частиц в растворе (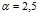 для сферических частиц;
для сферических частиц;  для эллиптических удлиненных частиц). Белки – это высокомолекулярные вещества, но в водных растворах как отдельные молекулы белка, так и белковые глобулы взаимодействуют с растворителем. Поэтому для описания обнаруженной экспериментально линейной зависимости вязкости растворов белков от концентрации можно применить уравнение Эйнштейна с поправкой на значения и физический смысл коэффициентов. На рис. 3 представлены концентрационные зависимости относительной вязкости для водных растворов альбумина и интерферона альфа лейкоцитарного человеческого. Прямо пропорциональное соотношение относительной вязкости раствора и массовой доли альбумина или интерферона альфа лейкоцитарного человеческого в растворе позволяет описывать данную закономерность уравнением, аналогичным уравнению Эйнштейна:
для эллиптических удлиненных частиц). Белки – это высокомолекулярные вещества, но в водных растворах как отдельные молекулы белка, так и белковые глобулы взаимодействуют с растворителем. Поэтому для описания обнаруженной экспериментально линейной зависимости вязкости растворов белков от концентрации можно применить уравнение Эйнштейна с поправкой на значения и физический смысл коэффициентов. На рис. 3 представлены концентрационные зависимости относительной вязкости для водных растворов альбумина и интерферона альфа лейкоцитарного человеческого. Прямо пропорциональное соотношение относительной вязкости раствора и массовой доли альбумина или интерферона альфа лейкоцитарного человеческого в растворе позволяет описывать данную закономерность уравнением, аналогичным уравнению Эйнштейна: 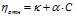 . Значения коэффициентов
. Значения коэффициентов 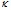 и
и 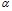 для альбумина и интерферона представлены в таблице 2.
для альбумина и интерферона представлены в таблице 2.
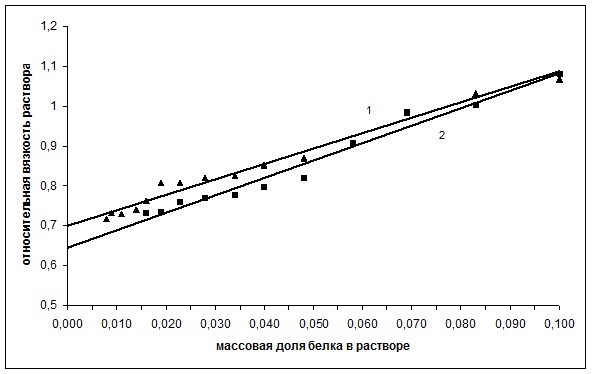
Рис. 3. Зависимость относительной вязкости раствора от массовой доли интерферона альфа лейкоцитарного человеческого (1) и альбумина (2).
Таблица 2
Значения коэффициентов в уравнении 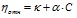 и коэффициенты корреляции
и коэффициенты корреляции
для концентрационных зависимостей относительной вязкости альбумина
и интерферона альфа лейкоцитарного человеческого
|
Белок |
Коэффициент |
Коэффициент |
Коэффициент корреляции |
|
Альбумин |
0,645 |
4,366 |
|
|
Интерферон |
0,701 |
3,856 |
|
Как следует из приведенных экспериментальных результатов, значения коэффициентов 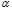 для альбумина и интерферона альфа лейкоцитарного человеческого превышают 2,5. Исходя из классического уравнения Эйнштейна [6], это означает, что в исследуемых водных растворах белков частицы вытянутые эллипсообразные. Однако в [2; 3] однозначно доказано существование только сферической глобулярной конформации макромолекул альбумина и интерферона альфа лейкоцитарного человеческого в водных растворах с концентрацией белка до 10%. Непротиворечиво объяснить такое расхождение данных можно, если допустить, что коэффициенты
для альбумина и интерферона альфа лейкоцитарного человеческого превышают 2,5. Исходя из классического уравнения Эйнштейна [6], это означает, что в исследуемых водных растворах белков частицы вытянутые эллипсообразные. Однако в [2; 3] однозначно доказано существование только сферической глобулярной конформации макромолекул альбумина и интерферона альфа лейкоцитарного человеческого в водных растворах с концентрацией белка до 10%. Непротиворечиво объяснить такое расхождение данных можно, если допустить, что коэффициенты 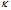 и
и 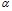 имеют несколько иной физический смысл, чем коэффициенты классического уравнения Эйнштейна. Коэффициент
имеют несколько иной физический смысл, чем коэффициенты классического уравнения Эйнштейна. Коэффициент 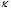 отличен от единицы, и его значение свидетельствует о том, что вязкость растворов белка ниже, чем вязкость чистой воды, при незначительных концентрациях белка. Значение коэффициента
отличен от единицы, и его значение свидетельствует о том, что вязкость растворов белка ниже, чем вязкость чистой воды, при незначительных концентрациях белка. Значение коэффициента 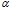 определяется не только формой частиц в растворе, но и уровнем сольватации белковых макромолекул в глобуле. Оба коэффициента
определяется не только формой частиц в растворе, но и уровнем сольватации белковых макромолекул в глобуле. Оба коэффициента 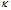 и
и 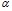 отражают влияние на вязкость системы молекулярной массы белка и уровня взаимодействия белковых макромолекул между собой и с растворителем.
отражают влияние на вязкость системы молекулярной массы белка и уровня взаимодействия белковых макромолекул между собой и с растворителем.
Как показано в [4] на примере водных растворов иммуноглобулина нормального, если конформация белковых глобул отлична от сферической, т.е. белковые глобулы анизодиаметричны, то линейная корреляция между концентрацией и вязкостью нарушается, и концентрационная зависимость вязкости для иммуноглобулина нормального удовлетворительно аппроксимируется полиномом второй степени.
Детальное изучение коллигативных свойств водных растворов иммуноглобулина нормального дало возможность выявить область концентраций (5-6%), в которой происходит изменение формы белковых глобул. Нарушение глобулярной сферической конформации и возможный ее переход в глобулярную эллиптическую сопровождается соответствующими изменениями коллигативных свойств растворов [4]. Для водных растворов иммуноглобулина нормального (3,5–4%) вязкость выше, чем для растворов альбумина и интерферона соответствующих концентраций, и начиная с концентрации 6% возрастает быстрее, чем это определено по линейному закону. Это полностью согласуется с литературными данными [6], согласно которым вязкость растворов высокомолекулярных веществ возрастает с увеличением асимметрии их частиц и с увеличением молекулярной массы.
Линейные закономерности изменения коллигативных свойств водных растворов белков (альбумина, интерферона альфа лейкоцитарного человеческого, иммуноглобулина нормального, иммуноглобулина противоклещевого, интерферона альфа лейкоцитарного человеческого) могут быть использованы для лабораторного экспрессного контроля содержания индивидуальных белков в лекарственных формах [2–4]. В ряду экспрессных лабораторных методов контроля, не требующих дорогостоящего поверенного оборудования и большого объема пробы для определения, находится метод рефрактометрии. Концентрационные зависимости показателя преломления водных растворов для альбумина и интерферона альфа лейкоцитарного человеческого представлены на рис. 4. Как следует из представленных данных, показатель преломления водного раствора линейно возрастает с увеличением концентрации белка. Уравнения регрессии имеют вид: 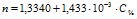 (
(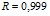 ) для интерферона альфа лейкоцитарного человеческого и
) для интерферона альфа лейкоцитарного человеческого и 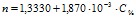 (
(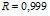 ) для альбумина. Свободный член уравнений регрессии представляет собой показатель преломления воды. Поэтому в общем виде найденная зависимость может быть представлена как
) для альбумина. Свободный член уравнений регрессии представляет собой показатель преломления воды. Поэтому в общем виде найденная зависимость может быть представлена как 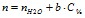 . В отличие от концентрационных зависимостей вязкости добавление небольших количеств белка в водный раствор не изменяет скачкообразно рефрактометрические свойства, а происходит линейное повышение показателя преломления начиная со значения для чистой воды.
. В отличие от концентрационных зависимостей вязкости добавление небольших количеств белка в водный раствор не изменяет скачкообразно рефрактометрические свойства, а происходит линейное повышение показателя преломления начиная со значения для чистой воды.
Аналогично угловой коэффициент b в уравнениях прямой отражает влияние природы растворенного вещества и его молекулярной массы на показатель преломления раствора. На качественном уровне: чем выше молекулярная масса белка, тем выше показатель преломления раствора при одной и той же концентрации вещества.
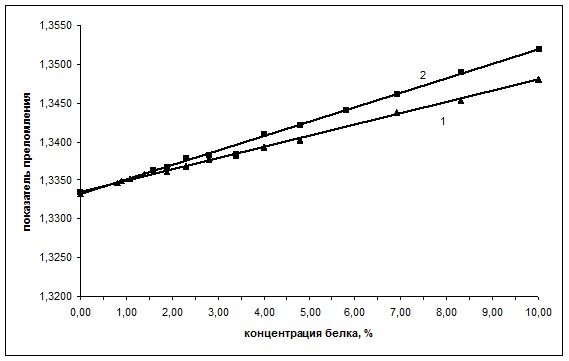
Рис. 4. Зависимость показателя преломления раствора от массовой доли интерферона альфа лейкоцитарного человеческого (1) и альбумина (2).
Выводы
- Опытным путем установлено, что концентрационные зависимости кинематической, динамической и относительной вязкости водных растворов белков – альбумина и интерферона альфа лейкоцитарного человеческого – подчиняются линейным законам. Это позволяет применить уравнение, аналогичное классическому уравнению Эйнштейна, для описания закономерностей изменения вязкости в растворах указанных препаратов с поправкой на физический смысл и значения коэффициентов.
- Рассчитанные значения коэффициентов в уравнении Эйнштейна для альбумина и интерферона альфа лейкоцитарного человеческого отличны от классических и отражают влияние уровня межмолекулярного взаимодействия в растворе, молекулярной массы белка и формы и размера белковых глобул на вязкость водных растворов.
- С увеличением концентрации белков происходит линейное увеличение показателя преломления растворов, что однозначно определяет место метода рефрактометрии, как одно из лидирующих, для лабораторного экспрессного контроля содержания индивидуальных белков в лекарственных формах.
Рецензенты:
Смолко В.А., д.т.н., заведующий кафедрой неорганической химии, профессор; ФГБОУ ВПО «Южно-Уральский государственный университет» (национальный исследовательский университет), г. Челябинск;
Колесников О.Л., д.м.н., профессор, заведующий кафедрой биологии, ГБОУ ВПО «Южно-Уральский государственный медицинский университет», г. Челябинск.




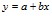 и коэффициент корреляции
и коэффициент корреляции