Расчет установившихся режимов является одной из главных задач, решаемых при проектировании и эксплуатации электрических сетей. Стандартные математические модели учитывают нелинейность, вносимую потребителями энергии, однако параметры схемы замещения электрической сети обычно задаются в линейной форме. Вместе с тем для этих параметров также характерны различные виды нелинейности, среди которых наиболее важное значение имеет температурная зависимость активных сопротивлений продольных ветвей.
В настоящее время основной областью учета данного фактора в электроэнергетике является расчет потерь энергии. Однако температурная зависимость сопротивления учитывается обычно только на стадии вычисления потерь как функции токов или передаваемых мощностей; сами токи и мощности в большинстве случаев определяются без учета температуры. Данное положение обусловлено тем, что если нагрузочные потери прямо пропорциональны активным сопротивлениям, то для токов и мощностей активные сопротивления элементов сети являются менее значимым фактором, часто рассматриваемым как вторичный. Действительно, схемы замещения электрических сетей содержат не только активные, но и индуктивные сопротивления, причем последние во многих случаях преобладают. Кроме того, если сеть разомкнута, то потокораспределение вообще мало зависит от параметров элементов сети и определяется в основном нагрузками.
Тем не менее функциональные связи между параметрами режима электрических систем имеют сложный и нелинейный характер, и предсказать степень влияния отдельных факторов на результаты расчета в каждой конкретной ситуации достаточно трудно. Поэтому разработки в области учета температурной зависимости сопротивлений при расчете режимов существуют [9, 2, 5-7].
В настоящей статье также предлагается один из вариантов решения данной задачи. Определение температуры производится на основе уточненных уравнений теплового баланса воздушных линий, учитывающих солнечную радиацию. При этом в качестве объекта расчетов выбрана сеть с двухсторонним питанием. Данный выбор обусловлен тем, что в замкнутых сетях, в отличие от разомкнутых, сопротивления элементов оказывают принципиальное влияние на потокораспределение. Кроме того, при изменении активных сопротивлений меняется степень однородности сети, что должно непосредственно сказываться на величине потерь энергии.
1. Математические модели. Сеть с двухсторонним питанием и ее схема замещения показаны на рис. 1, 2. Математическая модель установившегося режима, учитывающая температурную зависимость сопротивлений, может быть записана в следующем виде:
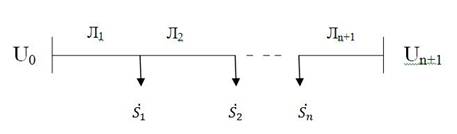
Рис . 1. Сеть с двухсторонним питанием
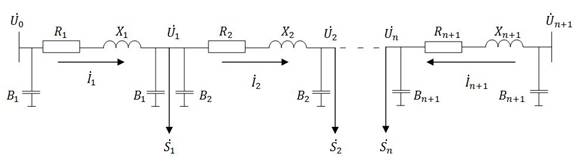
Рис. 2. Схема замещения
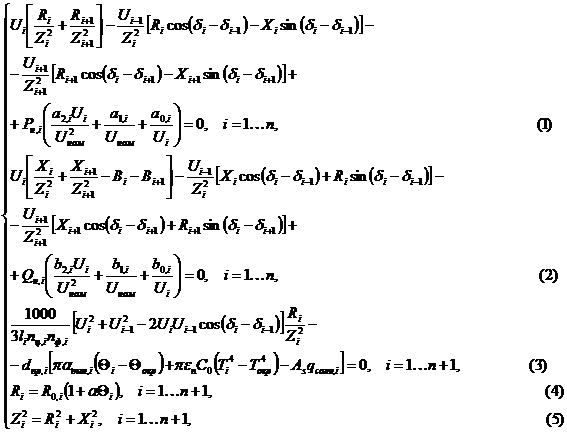
где Ui, δi – модули и фазы напряжений в узлах, кВ и рад; Pн,i, Qн,i – мощности потребителей, МВт и Мвар, при условии, что напряжение в соответствующем узле равно Uном, кВ; a2,i, a1,i, a0,i, b2,i, b1,i, b0,i – коэффициенты квадратичной аппроксимации статических характеристик активной и реактивной мощности нагрузок по напряжению; li – длина линии, км; nц,i и nф,i – число цепей линии и число проводов в фазе; dпр,i – диаметр провода, м; αвын,i – коэффициент теплоотдачи провода (вынужденной конвекцией), Вт/(м2∙°C); Θi, Θокр – температуры провода и окружающей среды, °C; Ti, Tокр – абсолютные температуры провода и окружающей среды; εп и As – степень черноты поверхности провода и поглощательная способность поверхности для солнечного излучения; C0 = 5,67∙10-8 Вт/(м2∙K4) – постоянная Стефана – Больцмана: qсолн,i – плотность потока солнечной радиации на поверхность провода, Вт/м2; R0,i – активное сопротивление линии, Ом, при 0 °C; α – температурный коэффициент сопротивления.
Уравнения (1), (2) представляют собой стандартные уравнения узловых напряжений в форме баланса токов в полярной системе координат. Собственные и взаимные проводимости узлов расписаны через сопротивления и емкостные проводимости линий. Это сделано для того, чтобы в уравнения в явном виде входили нелинейные элементы – активные сопротивления.
Кроме уравнений электрического режима (1), (2) система включает в себя уравнения теплового баланса воздушных линий (3). Первое слагаемое в этих уравнениях представляет собой потери активной мощности в одном проводе длиной 1 м, выраженные в [Вт]. Для перевода потерь во всей линии в [МВт] в указанную величину используется множитель перед квадратной скобкой. Выражение в квадратных скобках в рассматриваемом слагаемом представляет собой квадрат модуля падения напряжения в линии. Второе слагаемое определяет тепловой поток от провода, обусловленный конвекцией и тепловым излучением, за вычетом солнечной радиации, записанный аналогично [9].
Выражения (4) и (5) представляют собой формулы связи уравнений электрического и теплового режимов, определяющие температурную зависимость активных сопротивлений (4) и квадраты полных сопротивлений (5). Эти формулы выписаны отдельно только для наглядности и сокращения записи основных уравнений; в действительности при решении системы формулы (4), (5) подставляются в уравнения (1), (2) и (3). При этом общая размерность системы становится равной (3n+1), и неизвестными в ней являются модули и фазы напряжений Ui, δi, а также температуры проводов Θi.
Особенностью и недостатком данной модели является множественность решений. Так, каждое из уравнений теплового баланса имеет по меньшей мере два действительных решения, и столько же решений обычно имеет нелинейная система уравнений электрического режима (при заданных сопротивлениях). Тогда общее число решений можно оценить как 2(n+1)2, причем только два из них имеют физический смысл, а остальные являются чистой математической абстракцией. Чтобы избежать этого, можно использовать упрощенную форму записи уравнений теплового баланса [9], которая исключает «посторонние» решения:
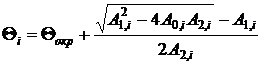 , (6)
, (6)
где
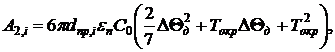 (7)
(7)
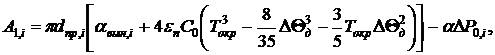 (8)
(8)
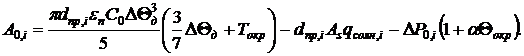 (9)
(9)
Здесь ΔΘд = Θдоп - Θокр – превышение допустимой температуры провода над температурой окружающей среды; ΔP0,i – потери мощности в проводе длиной 1 м, которые имели бы место при фактическом токе и при температуре провода 0 °C [9]. Выражая эти потери через модули и фазы напряжений, получим:
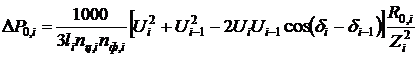 . (10)
. (10)
Заменив уравнение (3) на (6) с учетом (7)-(10), получим математическую модель режима, число решений в которой уменьшено до двух (если система уравнений узловых напряжений при постоянных сопротивлениях имеет 2 решения). При этом оба решения имеют физический смысл.
2. Выбор методов решения систем уравнений. При расчете режимов электрических сетей наиболее часто используется метод Ньютона. Естественным решением было бы непосредственное применение этого же метода для модели, учитывающей температуру, например (1)-(5). Однако уравнения теплового баланса резко отличаются от уравнений узловых напряжений, в результате чего можно ожидать ухудшения сходимости вычислительного процесса. В частности, если токи далеки от допустимых по нагреву, то влияние температуры на электрический режим будет слабым, что приведет к плохой обусловленности матрицы Якоби (в той части, которая соответствует уравнениям теплового баланса и производным по температуре).
Чтобы избежать этого, в основу алгоритма можно положить решение методом Ньютона только уравнений узловых напряжений, а влияние температуры учитывать как дополнительный уточняющий фактор. При этом возможны два подхода.
1. Организация двойного итерационного процесса: внутренний цикл – решение уравнений узловых напряжений; внешний цикл – уточнение температуры. Подобного рода алгоритмы описаны в работах к.т.н., доцента Барскова В.В.
2. Уточнение температуры на каждой итерации метода Ньютона при очередном расчете элементов матрицы Якоби. Другими словами, температурная коррекция вводится «внутрь» метода Ньютона.
Общее описание и характеристики рассматриваемых методов сведены в (табл. 1).
Таблица 1
Численные методы расчета режима сети с учетом температуры
|
Название метода |
Совместное решение уравнений |
Двойной итерационный процесс |
Внутренняя температурная коррекция |
|
Краткое описание |
Уравнения узловых напряжений и теплового баланса решаются как единая система методом Ньютона. |
1. Задание начальных приближений температур. 2. Расчет активных сопротивлений. 3. Решение уравнений узловых напряжений методом Ньютона. 4. Расчет следующих приближений температур и возврат в пункт 2. |
На каждой итерации решения уравнений узловых напряжений методом Ньютона производится уточнение температур и активных сопротивлений путем решения уравнений теплового баланса. При этом элементы матрицы Якоби и правые части линеаризованных уравнений узловых напряжений вычисляются с учетом изменения активных сопротивлений. |
|
Порядок матрицы Якоби |
3n+1 |
2n |
2n |
Каждый из этих методов в принципе может быть использован как для модели без упрощений (1)-(5), так и для модели с квадратичной аппроксимацией (1), (2), (4)-(10). Однако совместное решение методом Ньютона уравнений (1), (2), (4)-(10) вместо (1)-(5) приводит не к упрощению, а к усложнению расчетов, так как, несмотря на аппроксимацию, система все равно остается нелинейной, а температура определяется по более громоздким выражениям. В то же время в двух других методах расчет температур выделен в отдельную вычислительную процедуру. Поэтому использование квадратичной аппроксимации в этих случаях приводит к существенному уменьшению объема расчетов: температуры определяются аналитически, а не численно. При этом потери точности практически не происходит [9].
Таким образом, метод совместного решения уравнений целесообразно применять для модели без упрощений, а метод внутренней температурной коррекции – для модели с квадратичной аппроксимацией.
Ниже приведены результаты соответствующих расчетов. При этом, хотя метод двойного итерационного процесса также может быть использован для модели с квадратичной аппроксимацией, при сравнительных расчетах была использована модель с упрощенными уравнениями теплового баланса [4]. Это не сказывается на сходимости, зато позволяет дополнительно оценить влияние точности уравнений на результаты расчета режимов.
3. Анализ результатов. Для сравнения методов между собой, а также с классическим методом, не учитывающим температуру, было рассмотрено четыре характерных режима (табл. 2, 3) сети с тремя линиями (n=2).
Таблица 2
Характеристика режимов, длины линий и марки проводов
|
№ режима |
Характеристика |
Марки проводов, длины линий |
||
|
Л1, 40 км |
Л2, 50 км |
Л3, 60 км |
||
|
1 |
Однородная сеть с невысоким отношением сопротивлений X/R, большие нагрузки |
АС-70 |
АС-70 |
АС-70 |
|
2 |
Однородная сеть с высоким X/R, большие нагрузки |
АС-240 |
АС-240 |
АС-240 |
|
3 |
Неоднородная сеть, большие нагрузки |
АС-240 |
АС-70 |
АС-70 |
|
4 |
Однородная сеть с невысоким X/R, небольшие нагрузки |
АС-70 |
АС-70 |
АС-70 |
Таблица 3
Мощности нагрузок и напряжения источников питания
|
№ режима |
Pн,1, МВт |
Pн,2, МВт |
Qн,1, Мвар |
Qн,2, Мвар |
U0, кВ |
|
|
1 |
55 |
55 |
29 |
25 |
120 |
120 |
|
2 |
125 |
125 |
65 |
75 |
121 |
|
|
3 |
100 |
75 |
60 |
35 |
120 |
|
|
4 |
30 |
45 |
20 |
25 |
120 |
|
Нагрузки заданы пологими статическими характеристиками с коэффициентами a1=0,4; a2=0; a0=0,6; b1=-18; b2=10; b0=9 [3] (такой вариант учитывает влияние напряжения на потребляемые мощности и в то же время достаточно близок к классическому способу задания нагрузок постоянной мощностью).
Условия охлаждения и параметры проводов приведены в (табл. 4, 5).
Таблица 4
Условия охлаждения
|
Параметр |
Численное значение или расчетная формула |
|
Температура окружающей среды Θокр |
-10 ºC |
|
Атмосферное давление Pатм |
100000 Па |
|
Скорость ветра V |
1 м/с |
|
Коэффициент угла атаки ветра kV для линии 1 |
0,75 |
|
Коэффициент угла атаки ветра kV для линий 2, 3 |
1 |
|
Плотность потока прямой солнечной радиации на поверхность, перпендикулярную солнечным лучам qs,пр |
500 Вт/м2 |
|
Плотность потока рассеянной солнечной радиации qs,расс |
100 Вт/м2 |
|
Коэффициент kзт, учитывающий затененность участков линий 1, 2 |
0,8 |
|
Коэффициент kзт, учитывающий затененность участков линии 3 |
0,7 |
|
Угол между осью провода и направлением солнечных лучей φs для линии 1 |
π/4 |
|
Угол между осью провода и направлением солнечных лучей φs для линий 2, 3 |
π/5 |
|
Коэффициенты теплоотдачи αвын |
|
|
Плотности потока солнечной радиации на поверхности проводов qсолн |
|
Таблица 5
Расчетные параметры проводов [9], [10]
|
Параметр |
АС-70/11 |
АС-240/32 |
|
Диаметр провода dпр |
0,0114 м |
0,0216 м |
|
Погонное активное сопротивление при 20°C r20 |
0,422 Ом/км |
0,118 Ом/км |
|
Погонное активное сопротивление при 0°C r0 = r20 / (1+a∙20) |
0,3886 Ом/км |
0,1087 Ом/км |
|
Погонное индуктивное сопротивление x0 |
0,444 Ом/км |
0,405 Ом/км |
|
Погонная емкостная проводимость b0 |
2,547 мкСм/км |
2,808 мкСм/км |
|
Температурный коэффициент сопротивления a |
0,0043 ºC-1 |
|
|
Степень черноты поверхности провода εп |
0,6 |
|
|
Поглощательная способность поверхности провода для солнечного излучения As |
0,6 |
|
|
Допустимая температура провода Θдоп |
70 ºC |
|
В (табл. 6, 7) представлены результаты расчета режимов. Нумерация режимов соответствует таблице 2. Методы расчета пронумерованы следующим образом: 1 – совместное решение уравнений, модель без упрощений; 2 – двойной итерационный процесс, модель с упрощенными уравнениями теплового баланса [4]; 3 – внутренняя температурная коррекция, модель с квадратичной аппроксимацией; 4 – стандартный метод, не учитывающий температуру.
Таблица 6
Напряжения и токи, число итераций
|
№ режима |
№ метода |
|
|
I, А |
Число итераций |
||
|
Л1 |
Л2 |
Л3 |
|||||
|
1 |
1 |
|
|
365,1 |
36,74 |
290 |
26 |
|
2 |
|
|
367,3 |
38,92 |
285,8 |
14 |
|
|
3 |
|
|
365,1 |
36,73 |
290 |
7 |
|
|
4 |
|
|
369,7 |
41,91 |
281,1 |
3 |
|
|
2 |
1 |
|
|
848,2 |
100,8 |
726,4 |
13 |
|
2 |
|
|
847,8 |
104 |
724,3 |
16 |
|
|
3 |
|
|
848,2 |
100,8 |
726,4 |
6 |
|
|
4 |
|
|
845,1 |
105,5 |
720,3 |
4 |
|
|
3 |
1 |
|
|
727,5 |
148,9 |
416,6 |
21 |
|
2 |
|
|
729 |
151,9 |
416 |
17 |
|
|
3 |
|
|
727,5 |
148,9 |
416,6 |
7 |
|
|
4 |
|
|
698,7 |
126,3 |
424,5 |
4 |
|
|
4 |
1 |
|
|
265,5 |
84,46 |
201,5 |
21 |
|
2 |
|
|
266,6 |
86,04 |
200,9 |
9 |
|
|
3 |
|
|
265,5 |
84,46 |
201,5 |
6 |
|
|
4 |
|
|
268,6 |
87,54 |
199,3 |
3 |
|
Таблица 7
Температуры и потери мощности
|
№ режима |
№ метода |
Потери активной мощности, кВт |
Θ, ºC |
|||||
|
Л1 |
Л2 |
Л3 |
сумма |
Л1 |
Л2 |
Л3 |
||
|
1 |
1 |
8068 |
76,6 |
6526 |
14671 |
69,31 |
-6,142 |
25,42 |
|
2 |
7611 |
84,7 |
6275 |
13971 |
48,8 |
-9,459 |
22,78 |
|
|
3 |
8069 |
76,58 |
6526 |
14672 |
69,36 |
-6,159 |
25,43 |
|
|
4 |
6923 |
111,2 |
6001 |
13035 |
- |
- |
- |
|
|
2 |
1 |
12178 |
162 |
11757 |
24098 |
69,25 |
-5,07 |
32,3 |
|
2 |
11444 |
169,5 |
11691 |
23305 |
51,32 |
-9,24 |
32,35 |
|
|
3 |
12181 |
162 |
11758 |
24100 |
69,31 |
-5,086 |
32,3 |
|
|
4 |
10113 |
197 |
11019 |
21329 |
- |
- |
- |
|
|
3 |
1 |
8299 |
1299 |
15742 |
25340 |
47,01 |
1,187 |
68,94 |
|
2 |
7916 |
1336 |
15761 |
25013 |
32,99 |
-1,506 |
70,19 |
|
|
3 |
8299 |
1300 |
15743 |
25341 |
46,99 |
1,194 |
68,98 |
|
|
4 |
6912 |
1009 |
13688 |
21610 |
- |
- |
- |
|
|
4 |
1 |
3714 |
408,4 |
2936 |
7057 |
30,13 |
-4,148 |
7,836 |
|
2 |
3572 |
417,9 |
2887 |
6878 |
18,07 |
-7,334 |
5,236 |
|
|
3 |
3714 |
408,4 |
2936 |
7058 |
30,13 |
-4,157 |
7,85 |
|
|
4 |
3653 |
485,1 |
3017 |
7155 |
- |
- |
- |
|
Из таблицы 6 видно, что наиболее медленную сходимость в среднем имеет метод № 1 – совместное решение уравнений электрического и теплового режима методом Ньютона. Метод № 2 – двойной итерационный цикл – обладает более быстрой сходимостью. Исключение – режим № 2, однако с учетом размерностей матрицы Якоби число вычислительных операций по методу № 2 в этом режиме также меньше, чем по методу № 1.
Наиболее хорошую сходимость из всех методов, учитывающих температуру, проявляет метод № 3 – внутренняя температурная коррекция.
Результаты расчета по моделям № 1 и 3 практически не отличаются друг от друга, что дополнительно подтверждает выводы, сделанные в [7]. В то же время модель № 2 дает существенно другие результаты. Это связано главным образом с тем, что данная модель не учитывает солнечную радиацию и направление ветра. Погрешности метода № 4 (не учитывающего температуру) относительно метода № 3 приведены в табл. 8.
Таблица 8
Погрешности расчета режимов, обусловленные неучетом температуры (по данным табл. 6 и 7)
|
Параметр |
Отклонение напряжения в узле от номинального U-Uном |
Ток в линии I |
Потери активной мощности в линии ΔPл |
Суммарные потери активной мощности ΔPΣ |
|
Средний модуль погрешности |
12,5% |
4,3% |
15,6% |
9,69% |
|
Максимальная погрешность |
-25,4% |
-15,2% |
45,2% |
-14,7% |
Как и следовало ожидать, наибольшие погрешности наблюдаются для потерь активной мощности. Эти погрешности обусловлены двумя факторами: неточностью определения значений активных сопротивлений и неточностью определения значений токов. Проанализируем взаимное влияние этих факторов на примере режимов № 3, в котором наблюдалась наибольшая погрешность расчета суммарных потерь (-14,7 %). Для этого определим потери, которые наблюдались бы при фактических температурах (определенных методом № 3), но при токах, вычисленных без учета температурной зависимости сопротивлений (методом № 4):
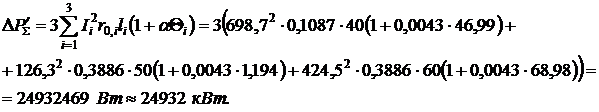
Полученное значение больше, чем потери, рассчитанные без учета температурной зависимости сопротивления методом № 4 (21610 кВт), но не достигает точного значения потерь, рассчитанного методом № 3 (25341 кВт). Это значит, что неточности вычисления токов и активных сопротивлений в данном случае не компенсируют, а усиливают друг друга, приводя к повышению результирующей погрешности.
На основании изложенного материала можно сделать следующие выводы:
1. Неучет температурной зависимости активных сопротивлений при расчете режимов замкнутых сетей может приводить к значительным погрешностям.
2. При моделировании тепловых режимов линий в рамках поставленной задачи целесообразно учитывать солнечную радиацию и направление ветра.
3. Совместное решение уравнений электрического и теплового режимов методом Ньютона неэффективно из-за медленной сходимости. Вместо этого может быть использован предложенный в настоящей статье метод внутренней температурной коррекции, обладающий улучшенной сходимостью.
Рецензенты:
Харламов В.В., д.т.н., профессор, заведующий кафедрой «Электрические машины и общая электротехника» Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Омский государственный университет путей сообщения», г. Омск;
Кузнецов А.А., д.т.н., профессор, заведующий кафедрой «Теоретическая электротехника» Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Омский государственный университет путей сообщения», г. Омск.




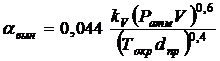 [6]
[6]