Тепловые расчеты элементов электрических сетей представляют собой практически важную задачу, поскольку температура определяет техническую допустимость того или иного электрического режима. Кроме того, учет температуры позволяет уточнить потери энергии.
Существует большое количество публикаций, посвященных тепловым расчетам линий электропередачи и связанным с этим задачам, например [1, 4, 6, 9]. В этих и других работах главным образом рассматриваются установившиеся температурные режимы. Это обусловлено тем, что допустимый ток определяется максимальным значением температуры, которое обычно достигается после завершения процесса нагрева.
Расчет потерь энергии с учетом температурной зависимости сопротивления базируется не на максимальном, а на среднем значении температуры. Чтобы точно вычислить среднюю температуру, требуется учитывать не только стационарные, но и нестационарные тепловые режимы, на которые, как правило, приходится значительная доля времени.
Возможны ситуации, когда стационарные тепловые режимы линий вообще отсутствуют, например, при резкопеременных нагрузках. В этих случаях расчет нестационарных тепловых режимов необходим не только для вычисления средних температур и потерь энергии, но и для определения максимальной температуры с целью проверки нагрузочной способности линии.
Передача тепла от провода в окружающую среду осуществляется путем конвекции и излучения. Согласно закону Стефана – Больцмана, интенсивность теплового излучения тела (провода) пропорциональна четвертой степени его абсолютной температуры. Поэтому уравнение теплового баланса провода нелинейно. В случае проводов воздушных линий интенсивность теплопередачи излучением соизмерима с интенсивностью конвективного теплообмена. В связи с этим расчет стационарных тепловых режимов воздушных линий производится с учетом рассмотренной нелинейности [1, 4, 6, 9].
Вместе с тем расчет нестационарных тепловых режимов проводов производится, как правило, на основе простой экспоненциальной зависимости, соответствующей линейному дифференциальному уравнению первого порядка. Такой подход неизбежно приводит к погрешностям [7]. Кроме того, возникает неопределенность в оценке величины постоянной времени нагрева. Вместе с тем численное решение нелинейного дифференциального уравнения позволяет получить лишь частные результаты, что затрудняет их анализ и обобщение.
1. Математическая модель. Уравнение нагрева (охлаждения) неизолированного провода воздушной линии на открытом воздухе может быть записано в следующем виде:
![]() (1)
(1)
где αвын – коэффициент теплоотдачи вынужденной конвекцией; εп – коэффициент черноты поверхности провода для инфракрасного излучения; C0 = 5,67·10-8 Вт/(м2·К4) – постоянная излучения абсолютно черного тела; Θ и Θокр – температуры соответственно провода и окружающей среды в ºC; T и Tокр – то же в K (абсолютные температуры); As – поглощательная способность поверхности провода для солнечного излучения; qсолн – плотность потока солнечной радиации на провод; dпр – диаметр провода; ![]() – потери активной мощности в проводе на единицу длины при Θ = 0 ºC; I – ток в проводе; r0 – погонное активное сопротивление провода при Θ = 0 ºC; α – температурный коэффициент сопротивления; C – теплоемкость провода на единицу длины.
– потери активной мощности в проводе на единицу длины при Θ = 0 ºC; I – ток в проводе; r0 – погонное активное сопротивление провода при Θ = 0 ºC; α – температурный коэффициент сопротивления; C – теплоемкость провода на единицу длины.
Данное уравнение получено из уравнения теплового баланса провода в стационарном режиме [9] путем введения в правую часть производной температуры по времени, умноженной на теплоемкость. Это слагаемое представляет собой мощность, расходуемую на нагрев провода. Второе слагаемое в правой части (1) соответствует мощности теплообмена между проводом и окружающей средой. Эта мощность включает три составляющих: теплоотдачу конвекцией, теплообмен излучением и солнечную радиацию. Нелинейность вносится теплообменом излучением (второе слагаемое в квадратных скобках), мощность которого согласно закону Стефана – Больцмана пропорциональна абсолютной температуре поверхности охлаждающегося тела (провода) в четвертой степени.
В [9] рассмотрено преобразование нелинейного уравнения теплового баланса к квадратичному виду на основе метода наименьших квадратов. Аналогичным образом можно поступить и с дифференциальным уравнением нагрева. В результате уравнение (1) преобразуется к следующей приближенной форме:
![]() (2)
(2)
Коэффициенты A1, A2, A3 определяются по формулам
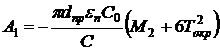 , 3)
, 3)
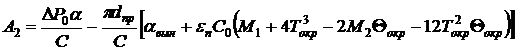 , (4)
, (4)
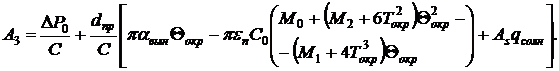 (5)
(5)
В приведенные формулы входят коэффициенты M1, M2, M0, которые получаются при преобразовании T4 методом наименьших квадратов к следующему выражению:
![]() (6)
(6)
Формулы для коэффициентов M1, M2, M0 имеют вид [6]
![]() , (7)
, (7)
![]() , (8)
, (8)
![]() . (9)
. (9)
Здесь ΔΘд = Θдоп – Θокр используется как диапазон температур, на котором производится преобразование; Θдоп – максимально допустимая температура провода.
Выражения (3)–(5) получаются при преобразовании (1) к (2) с учетом (6).
Уравнение (2) может иметь различные решения в зависимости от вида корней уравнения
![]() . (10)
. (10)
Возможны следующие случаи: 1) корни действительные и разные; 2) корни действительные и одинаковые; 3) корни комплексно-сопряженные. Поскольку данное алгебраическое уравнение описывает установившийся режим, то оно имеет действительные корни всегда, когда этот режим существует. В [2] на упрощенном примере рассмотрены случаи, когда установившегося режима не существует. Показано, что такая ситуация может возникнуть только при большой перегрузке линии, фактически в аварийном режиме. Кроме того, в [2] рассмотрена линейная модель. Расчеты для нелинейного (квадратичного) уравнения показали, что решение формально существует даже при очень больших токах. Объясняется это тем, что нелинейные составляющие теплового потока от провода возрастают при увеличении температуры гораздо быстрее, чем линейные, что способствует стабилизации режима. Однако необходимо заметить, что приведенные выше выкладки справедливы только для ограниченного (допустимого) диапазона температур, и выход за его пределы приводит к быстрому возрастанию погрешностей и в конце концов к потере адекватности модели.
Таким образом, случай комплексно-сопряженных корней может быть исключен из рассмотрения. Второй случай (корни действительные и одинаковые) представляет собой пограничную ситуацию, в связи с чем его также можно исключить.
Обозначим корни уравнения (10) следующим образом:
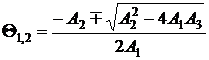 , (11)
, (11)
причем Θ1 > Θ2.
Тогда уравнение (2) имеет следующее решение:
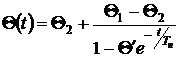 , (12)
, (12)
где введены обозначения
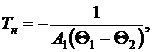 (13)
(13)
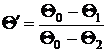 . (14)
. (14)
Здесь Θ0 – температура провода в момент времени t=0 (начальное условие). Решение (12) справедливо только в случае Θ0 > Θ2. Расчеты показали, что это условие выполняется (температура Θ2 имеет сильно отрицательные значения, обычно меньше не только температуры окружающей среды, но и абсолютного нуля).
Формула (12) описывает апериодический процесс, по форме сходный с обычной экспонентой. Однако если стандартная экспоненциальная функция (A+Be-t/T) задается тремя величинами (A, B, T), то для задания функции вида (12) требуется 4 величины (Θ1, Θ2, Θ0, Tн). Дополнительная четвертая величина определяет вклад нелинейного слагаемого.
Параметр Tн, как и постоянная времени в стандартной экспоненциальной функции, определяет временной масштаб (инерционность) процесса. Однако количественный смысл параметра Tн более сложен.
Средняя температура за некоторое время Tп получается путем интегрирования (12):
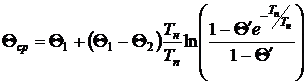 . (15)
. (15)
Тогда потери энергии за время Tп в трехфазной линии длиной l
![]() (16)
(16)
2. Анализ результатов. Ниже приведены результаты расчета теплового процесса в проводе АС-240/32 разработанным методом и методом Рунге – Кутта четвертого порядка. Расчетные условия приведены в (табл. 1). Параметры провода приняты согласно [1, 3, 10] (справочное значение сопротивления, приведенное к 20 ºC, пересчитано для температуры 0 ºC). В качестве параметров окружающей среды использована примерная совокупность возможных (реалистичных) значений. Коэффициент теплоотдачи и плотность потока солнечной радиации рассчитывались по следующим формулам [5, 8]:
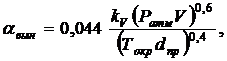 (17)
(17)
![]() . (18)
. (18)
Таблица 1
Условия, принятые при расчете теплового процесса в проводе АС-240/32
|
Наименование и обозначение параметра |
Численное значение |
|
Ток нагрузки I |
600 А |
|
Диаметр провода dпр |
0,0216 м |
|
Погонное активное сопротивление при 0°C r0 |
0,0001114 Ом/м |
|
Температурный коэффициент сопротивления a |
0,0043 ºC-1 |
|
Удельная теплоемкость алюминия Cуд,Al |
922 Дж/(кг∙ºC) |
|
Удельная теплоемкость стали Cуд,ст |
452 Дж/(кг∙ºC) |
|
Погонная масса алюминия MAl |
0,673 кг/м |
|
Погонная масса стали Mст |
0,248 кг/м |
|
Степень черноты поверхности провода εп |
0,6 |
|
Поглощательная способность поверхности провода для солнечного излучения As |
0,6 |
|
Температура окружающей среды Θокр |
10 ºC |
|
Атмосферное давление Pатм |
100000 Па |
|
Скорость ветра V |
1 м/с |
|
Коэффициент угла атаки ветра kV |
0,75 |
|
Плотность потока прямой солнечной радиации на поверхность, перпендикулярную солнечным лучам qs,пр |
500 Вт/м2 |
|
Плотность потока рассеянной солнечной радиации qs,расс |
100 Вт/м2 |
|
Коэффициент, учитывающий затененность участков линии kзт |
0,9 |
|
Угол между осью провода и направлением солнечных лучей φs |
45º |
|
Допустимая температура провода Θдоп |
70 ºC |
|
Температура провода в момент времени t=0 Θ0 |
10 ºC |
|
Расчетный период Tп |
60 мин |
|
Длина линии l |
50000 м |
Для расчета теплоемкости провода на единицу длины использовано очевидное выражение:
![]() . (19)
. (19)
Зависимости температуры провода от времени, полученные аналитическим и численным методом, представлены в виде таблицы (табл. 2) и рисунка. Расхождение результатов не превышает 0,01 ºC; в масштабе рисунка графики не различаются.
Таблица 2
Результаты расчета теплового процесса аналитическим (Θан) и численным (Θчс) методом
|
t, мин |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
16 |
20 |
24 |
|
Θан(t), ºC |
10 |
17,48 |
23,69 |
28,83 |
33,08 |
36,58 |
39,46 |
43,77 |
46,68 |
48,63 |
|
Θчс(t), ºC |
10 |
17,48 |
23,69 |
28,83 |
33,07 |
36,57 |
39,45 |
43,77 |
46,68 |
48,63 |
|
t, мин |
28 |
32 |
36 |
40 |
44 |
48 |
52 |
56 |
60 |
|
Θан(t), ºC |
49,93 |
50,81 |
51,4 |
51,79 |
52,05 |
52,22 |
52,34 |
52,42 |
52,47 |
|
Θчс(t), ºC |
49,94 |
50,82 |
51,4 |
51,8 |
52,06 |
52,23 |
52,35 |
52,43 |
52,48 |
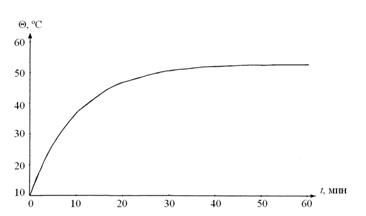
Результаты расчета теплового процесса в проводе АС-240/32
Средняя температура и потери энергии за расчетный период, вычисленные по формулам (15), (16), равны: Θср = 45,39 ºC; ΔW = 7189,7 кВт∙час.
Таким образом, видно, что разработанный аналитический метод по точности практически не отличается от численного и может быть рекомендован для практического использования.
Рецензенты:
Черемисин В.Т., д.т.н., профессор, директор Научно-исследовательского института энергосбережения на железнодорожном транспорте (НИИЭ ОмГУПС), заведующий кафедрой «Подвижной состав электрических железных дорог» ФГБОУ ВПО «Омский государственный университет путей сообщения», г. Омск;
Кандаев В.А., д.т.н., профессор кафедры «Инфокоммуникационные системы и информационная безопасность» ФГБОУ ВПО «Омский государственный университет путей сообщения», г. Омск.



