Практика работы отечественных и зарубежных промышленных предприятий свидетельствует о том, что батареи статических конденсаторов (БСК), работающие при несинусоидальном напряжении, в ряде случаев очень быстро выходят из строя в результате вспучиваний или взрывов. Причиной разрушения конденсаторов является постоянная перегрузка их токами высших гармоник (ВГ). Перегрузка происходит, как правило, при возникновении резонансного или близкого к нему режима на частоте какой-либо гармоники, имеющейся в амплитудном спектре напряжения сети. Резонансные контуры образуются ёмкостью БСК и индуктивностью сети [1].
Чтобы избежать преждевременного выхода из строя БСК в системах электроснабжения (СЭС), совместно с задачей компенсации реактивной мощности, где присутствуют электроприёмники, искажающие синусоидальность формы кривой напряжения и тока, должна решаться задача устранения эффекта резонанса.
Наиболее часто применяемый способ защиты БСК от негативного действия высших гармоник является применение последовательно включенных реакторов (индуктивных сопротивлений). Последнее время достаточно широко стали применяться бестрансформаторные шунтирующие активные фильтры [5]. В работе [4] авторы предлагают компенсацию реактивной мощности с устранением эффекта резонанса при помощи комбинированной системы. Установка представляет собой соединённые в треугольник группы однофазных инверторов без трансформаторной связи, подключаемых совместно с БСК.
Таким образом, продолжает оставаться актуальной задача расчета, анализа и моделирования резонанса токов в системах электроснабжения, что позволит оптимизировать режим с точки зрения коэффициента мощности и реализации технических мероприятий по подавлению гармоник. Однако при исследовании резонанса токов редко принимаются во внимание активные составляющие комплексных сопротивлений СЭС и изменение параметров нормального режима работы системы. Известно, что полностью «установившегося режима» реально существовать не может. Нагрузка в системе колеблется: непрерывно происходят малые изменения (флуктуации) числа подключенных потребителей – их мощности и состава. Подобные изменения могут оказать существенное влияние на режим резонанса токов. Кроме того, при наличии БСК с регулированием количество переменных величин в уравнении частоты резонанса увеличивается. На примере данной работы покажем необходимость учета вышеперечисленных факторов для расчета и моделирования резонанса токов в СЭС.
Общие теоретические положения
Резонанс токов, как известно из теории цепей, возникает при параллельном соединении ветвей с разнохарактерными реактивными сопротивлениями. Для исследования резонансных явлений в системах электроснабжения составим следующую схему (рисунок 1), которая представляет собой фрагмент схемы электроснабжения промышленного предприятия и отражает требуемые параметры.
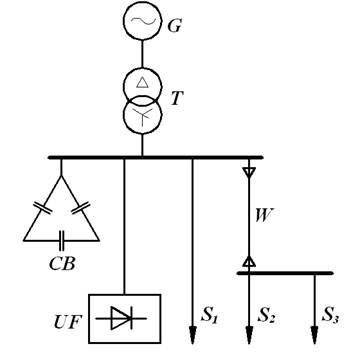
Рис. 1. Однолинейная схема электроснабжения:
G – источник электрической энергии (система), Т – трансформатор 10/0,4 кВ, СВ – силовые конденсаторные батареи компенсации реактивной мощности, UF – нелинейная нагрузка (преобразователь частоты), W – кабельная линия, S1, S2 и S3 – спокойные нагрузки.
Составим схему замещения исследуемой системы электроснабжения, необходимую для расчета цепи на высших гармонических составляющих (рис. 2).
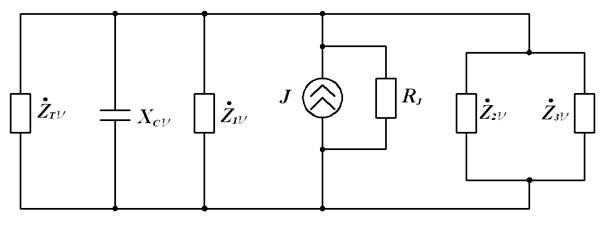
Рис. 2. Схема замещения на высших гармониках:
Z - полные сопротивления спокойных нагрузок и трансформатора, приведенного к напряжению 0,4 кВ, нелинейная нагрузка представлена источником тока J и внутренним сопротивлением RJ, силовые конденсаторные батареи учитываются их реактивным сопротивлением XC.
Схема замещения на рисунке 2 может быть посредством эквивалентных преобразований представлена как с источником тока (рис. 3а), так и эквивалентным источником ЭДС (рис. 3б), удобным для анализа режима резонанса токов
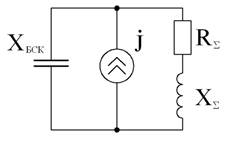а) 
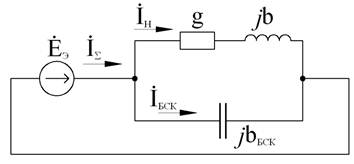б)
Рис. 3. Преобразование схемы замещения.
Ток нагрузки Iн имеет активно-индуктивный характер и отстает от ЭДС Eэ, может быть записан как:
, (1)
где 
– комплексное значение эквивалентной ЭДС, В
– комплексная проводимость эквивалентной схемы замещения, См;
– действительная часть комплексной проводимости ;
– мнимая часть.
По определению комплексной проводимости имеем:
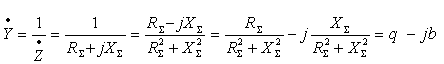(2)
; 
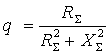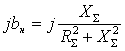(3)
При положительном значении X, значение b положительно. Если Х отрицательно, то b также отрицательно.
Ток в ветви БСК опережает ЭДС
. При 
→0, угол между током 
и ЭДС будет стремиться к 
.
(4)
Или при →0, т.е. 
→∞, имеем 
Ток в неразветвленной части цепи
(5)
По определению резонансного режима ток 
должен совпадать по фазе с напряжением 
. Это будет при условии, что сумма реактивных проводимостей ветвей равна нулю: 
В соответствии с (5):
; 
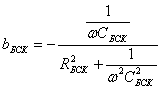
Или при учете →0, получаем 
.
Таким образом, условие наступления режима резонанса токов в схеме рис. 3 можно записать
(6)
Векторная диаграмма резонанса токов при →0 представлена на рисунке 4.
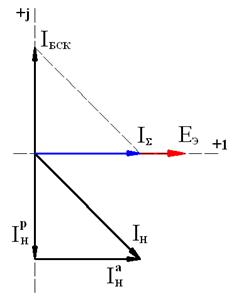
Рис. 4. Векторная диаграмма резонанса токов.
Если параметры Хн, Хбск заданы и режим работы электроприемников, подключенных к шинам подстанции, не меняется, а также отсутствует регулирование компенсации реактивной мощности (ступенчатое переключение БСК), то резонансную частоту можно определить из формулы (6):
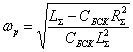(7)
Как было отмечено выше, при изменении мощности и характера электрических нагрузок и компенсации реактивной мощности регулируемыми БСК уравнение (7) будет иметь три переменных параметра: 
, 
и 
.
Математическое моделирование и численные эксперименты
Для проведения численного эксперимента в соответствии с заданной схемой примем некоторые значения нелинейной нагрузки (введена внутренним сопротивлением источника токаRj), общей нагрузки и трансформатора (табл. 1).
Таблица 1
Параметры схемы замещения
|
Общая нагрузка |
Нелинейная нагрузка |
Трансформатор |
Кабельная линия |
|||||
|
S1 |
S2 |
S3 |
UF |
Т |
W |
|||
|
кВА |
кВА |
кВА |
Rj ,Ом |
St, кВА |
Uкз, % |
Ркз, кВт |
r0, Ом/км |
x0, Ом/км |
|
100+95j |
20+15j |
40+35j |
2 |
400 |
4,5 |
5,5 |
0,869 |
0,0637 |
При расчетах учитывался характер изменения нагрузки, который фактически охватывал возможные комбинации сочетания одновременной работы нелинейной и общей нагрузки.
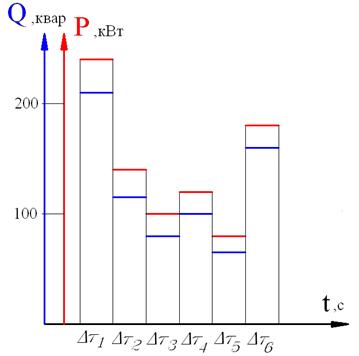
Рис. 5. График изменения нагрузок.
Интервалам времени соответствует комбинация одновременно работающих нагрузок (табл. 2).
Таблица 2
Комбинации нагрузок
|
Интервал времени |
Нагрузки, работающие в интервале времени |
|
Δτ1 |
S1 , S2 , S3 , UF |
|
Δτ2 |
S2 , S3 , UF |
|
Δτ3 |
S2 , UF |
|
Δτ4 |
S3 , UF |
|
Δτ5 |
UF |
|
Δτ6 |
S1 , UF |
Компенсация реактивной мощности осуществлялась до уровня tgφ≤0.35 [2], т.к. величина изменения уровня компенсации соответствовала шагу переключения БСК, равному 5000 вар.
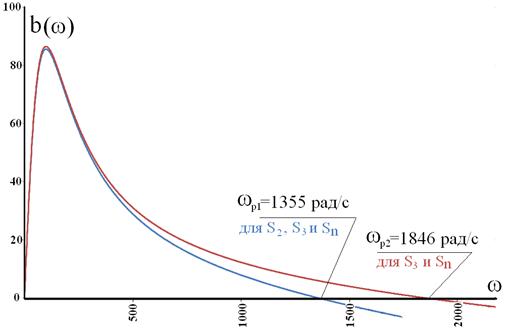
Рис. 6. АЧХ проводимости для двух интервалов времени: Δτ2 (синий) и Δτ4 (красный).
В результате численного моделирования переменной нагрузки получены значения резонансных частот для каждого интервала времени графика нагрузок (табл. 3).
Таблица 3
Резонансные частоты для каждого участка графика электрических нагрузок
|
Интервал времени |
Резонансная частота fp, Гц |
|
Δτ1 |
60,3 |
|
Δτ2 |
104,4 |
|
Δτ3 |
215,7 |
|
Δτ4 |
293,9 |
|
Δτ5 |
423,5 |
|
Δτ6 |
662,1 |
Выводы
Приведенные результаты численных экспериментов наглядно демонстрируют необходимость учета режима работы электроприёмников, активной проводимости схемы замещения и результатов применения регулирования ступеней БСК. Отсутствие учета данных факторов может привести к потере ряда частот, при которых наступает режим резонанса токов, а при наличии электроприёмников, являющихся источниками интергармоник, вообще к потере одного из резонансных режимов.
Как отмечалось в предыдущих работах [3], одним из инструментов при анализе режима резонанса токов может послужить вейвлет-анализ, позволяющий давать не только представление в частотном спектре, но и в амплитудно-временном виде. На рисунке 7 приведен пример разложения электроэнергетического сигнала при помощи вейвлет-анализа, где детализирующая составляющая сигнала показывает время изменения сигнала и гармонические составляющие в широком спектре сигналов.
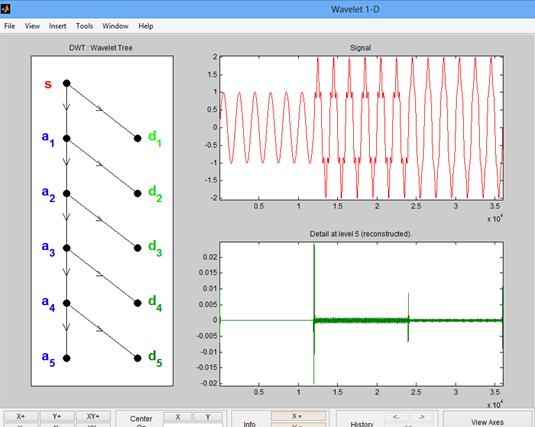
Рис. 7. Вейвлет-разложение сигнала.
Рецензенты:
Горелов В.П., д.т.н., профессор, заместитель зав. кафедрой «Электроэнергетические системы и электротехника» Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Новосибирская государственная академия водного транспорта», г. Новосибирск;
Сальников В.Г., д.т.н., профессор кафедры «Электроэнергетические системы и электротехника» Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Новосибирская государственная академия водного транспорта», г. Новосибирск.