Усиление наклонных сечений осуществляется путем наклейки в приопорную зону внешней поперечной ФАП-арматуры одним из трех способов (рис. 1).
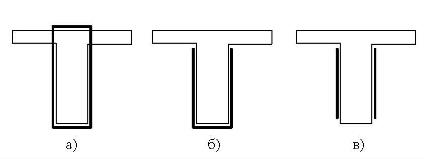
Рис. 1. Схемы наклейки внешней поперечной ФАП-арматуры: а) полное обертывание; б) усиление c трех сторон U-образным хомутом; в) усиление по двум сторонам.
Существующие методики расчета [3; 7; 10] были апробированы на однопролетных балках, там, где в приопорной зоне влияние изгибающего момента невелико. В реальных конструкциях многопролетные балки встречаются гораздо чаще, чем однопролетные, и влияние растягивающих напряжений в зоне усиления наклонных сечений может повлиять на прочность конструкции как в сторону запаса, так и в сторону дефицита прочности.
Для моделирования работы многопролетной железобетонной конструкции, усиленной полимерным материалом по наклонному сечению, выполнен численный эксперимент в программной системе конечно-элементного анализа Ansys. Для решения линейных и нелинейных, стационарных и нестационарных пространственных задач механики деформируемого твёрдого тела и механики конструкций (включая нестационарные геометрически и физически нелинейные задачи контактного взаимодействия элементов конструкций) применяется модуль Ansys Mechanical (APDL). Публикации последних лет отечественных [2; 4] и зарубежных [9] авторов указывают на достаточно точное воссоздание картины трещинообразования и вида разрушения при полном использовании всего функционала программы для моделирования железобетона.
В программном комплексе Ansys Mechanical моделировались 9 двухпролетных железобетонных балок длиной 2460 мм, сечением 120х220 (h) мм (рис. 2). Балки имеют одинаковые пролеты среза (300 мм), но различный шаг поперечной арматуры в зоне центральной опоры (0, 85 и 110 мм). Каждая из балок моделировалась в двух вариантах - с усилением и без. Усиление предусматривалось в пролете среза U-образными хомутами из углепластика холодного (площадочного) твердения. Хомуты устанавливались шириной 50 мм с шагом 100 мм. Схема усиления образцов представлена на рис. 2. Маркировка моделируемых балок представлена в таблице 1.
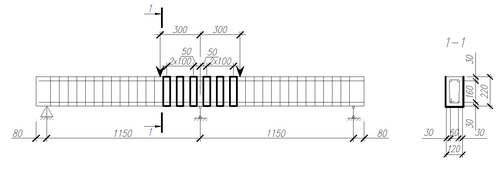
Рис. 2. Схема усиления железобетонных балок.
Таблица 1
Маркировка экспериментальных образцов балок
|
№ п/п |
Марка балки |
Поперечное армирование стальными стержнями в пролете среза |
Усиление внешними хомутами ФАП, ширина w, шаг s |
|
1 |
Бм-1.1 |
- |
- |
|
2 |
Бм-2.1 |
Ø6 с шагом 110 мм |
- |
|
3 |
Бм-3.1 |
Ø6 с шагом 85 мм |
- |
|
4 |
Бм-1.2 |
- |
w=50 мм, s=100 мм под углом 90° |
|
5 |
Бм-2.2 |
Ø6 с шагом 110 мм |
w=50 мм, s=100 мм под углом 90° |
|
6 |
Бм-3.2 |
Ø6 с шагом 85 мм |
w=50 мм, s=100 мм под углом 90° |
|
7 |
Бм-1.3 |
- |
w=50 мм, s=100 мм под углом α |
|
8 |
Бм-2.3 |
Ø6 с шагом 110 мм |
w=50 мм, s=100 мм под углом α |
|
9 |
Бм-3.3 |
Ø6 с шагом 85 мм |
w=50 мм, s=100 мм под углом α |
Усиление балок предусматривалось в двух вариантах - под углом 90° к продольной оси балки и под углом α. Угол α принимался как угол наклона главных площадок, определенный в ходе моделирования не усиленных образцов.
Для моделирования в численном эксперименте напряженно-деформированного состояния железобетонная балка и композиционный материал усиления разбиты на объемные (для моделирования бетона), плоские (композиционного материала) и стержневые элементы (для моделирования арматуры).
Бетон моделировался при помощи объемных конечных элементов solid65. В качестве критерия прочности выбрана модель Вильяма-Варнке [11], являющаяся развитием трехинвариантного критерия прочности Гениева [1].
Рассматриваются два основных механизма разрушения - от сжатия и от растяжения. Помимо модели прочности, также была использована диаграмма состояния, приведенная на рис. 3. Для обеспечения сходимости в данной модели бетона присутствуют некоторые коэффициенты, не имеющие четкого физического смысла, установление которых рекомендовано производителем КЭ-комплекса опытным путем. К ним относятся: коэффициенты передачи усилий через открытую и закрытую трещину, уровень трещин при растяжении. Значения данных коэффициентов приняты в соответствии с результатами сопоставления расчетов в программном комплексе Ansys с натурными экспериментами, проведенными на базе МГСУ в 2012 г. [4].
Из-за сложности определения фактической ширины раскрытия трещины методами КЭ-моделирования для обеспечения непрерывности сетки КЭ применяется метод «размазывания» зоны трещины на группу конечных элементов (smeared cracking). Поэтому в применяемой диаграмме состояния материала после достижения материалом предельных напряжений или деформаций требуется ввести условную ниспадающую ветвь (рис. 3). Таким образом, трещина в бетоне моделируется падением значения модуля деформаций при определенном уровне напряжений. Именно этот участок диаграммы моделирует распределение трещин по некоторой группе КЭ, давая, таким образом, возможность получить численное решение.
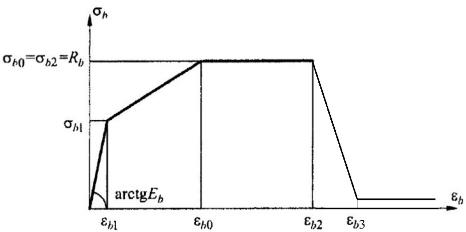
Рис. 3. Принятая диаграмма деформирования бетона
Моделирование стальной арматуры выполнено стержневыми конечными элементами link8. Для моделирования арматуры использована двухлинейная диаграмма Прандтля в соответствии с [5]. Композиционный материал усиления замоделирован при помощи оболочечных конечных элементов shell181, при этом его характеристики (толщина, модули упругости, модули сдвига) вводились как для системы усиления в целом (углепластиковое волокно совместно со связующим), данные характеристики приведены производителем в паспорте на систему усиления. Работа материала усиления предусмотрена только в упругой стадии. Связь между бетонной поверхностью и материалом усиления моделировалась при помощи элементов conta173, которые позволяют задать требуемый закон взаимодействия двух поверхностей. В качестве закона деформирования для conta173 принята двухлинейная диаграмма касательных напряжений, приведенная в [10] (рис. 4).
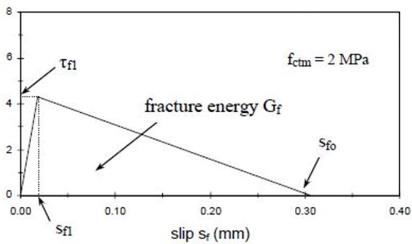
Рис. 4. Общий вид принятой диаграммы касательных напряжений по контакту «железобетон - композиционный материал»
Нагрузка на балку передавалась через стальные грузораспределительные пластины, которые смоделированы при помощи объемных конечных элементов solid185, для которых принят упругий закон деформирования.
Размер КЭ принят в соответствии с рекомендациями производителя программного комплекса [8] для подобных моделей - 1 см. Общий вид КЭ-модели представлен на рис. 5.
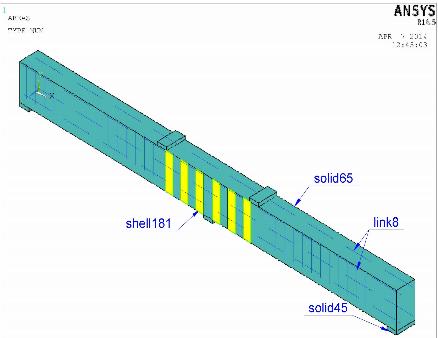
Рис. 5. Общий вид железобетонной балки, смоделированной в программном комплексе Ansys
Для расчета применялся неявный решатель дифференциальных уравнений. Поиск решения нелинейной задачи осуществлялся итерационным методом касательных (Ньютона-Рафсона) с автоматической оптимизацией шага приближения по мере решения. Для итерационного решателя в Ansys реализуется метод обусловленных сопряженных градиентов. Контроль сходимости осуществлялся для нагрузки с точностью 5%.
В результате численного эксперимента получены значения напряжений и деформаций на каждой стадии НДС, графики «прогиб - нагрузка». Анализ результатов показал, что для балок без поперечного армирования система усиления дает значительный прирост прочности (до 84%), тогда как для балок с поперечным армированием этот прирост гораздо меньше (до 12%), и чем интенсивнее армирование стальными хомутами, тем меньший эффект привносит система усиления. Бо́льший процент поперечного армирования позволяет балке достичь более высокого уровня нормальных напряжений в зоне средней опоры, не разрушаясь. Бетон в зоне средней опоры находится в плоском напряженном состоянии двухосного растяжения, и при определенном уровне нормальных растягивающих напряжений выкол бетона основания системы усиления происходит намного раньше исчерпания прочности самого материала усиления (рис. 6).
На изображениях изополей главных напряжений отчетливо видны зоны формирования критической наклонной трещины в балках без усиления. При этом в балках с поперечной арматурой образованию наклонных трещин предшествует раскрытие нормальных трещин над центральной опорой от действия нормальных растягивающих напряжений. В траектории раскрытия наклонной трещины заметно ее отклонение от линии «грузораспределительная пластина - опора» в сторону верха балки, т.е. в сторону действия максимальных нормальных растягивающих напряжений. На трехмерных изображениях изополей главных напряжений в усиленных балках заметны экстремумы главных напряжений на верхней грани балки, в зоне свободных концов хомутов усиления, причем по значению эти точки сравнимы с максимальными значениями главных напряжений в зоне образования критической наклонной трещины.
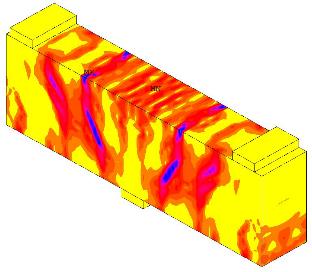
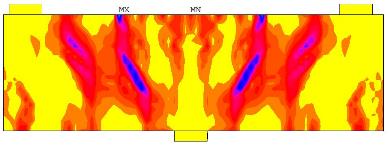
Рис. 6. Изополя главных растягивающих напряжений в усиленной балке с внутренним поперечным армированием (шаг 110 мм)
На основе проведенного численного эксперимента можно предполагать, что разрушение балок начинается с выкола бетона у свободного конца хомута внешнего армирования и продолжается формированием критической наклонной трещины, которая раскрывается от нейтральной оси к грузораспределительной пластине, через которую передается нагрузка.
Также численный эксперимент продемонстрировал, что с увеличением процента армирования стальной поперечной арматурой эффективность системы усиления снижается.
С учетом результатов численного эксперимента была составлена программа натурных испытаний. В ходе натурных экспериментов были определены прочностные и деформационные характеристики арматуры, бетона и материала усиления. Диаграммы деформирования, полученные на натурных образцах, были использованы для задания характеристик элементов при дальнейшем уточнении КЭ-модели. Сравнение графиков прогиба под центральной опорой приведено на рис. 7.
За условную разрушающую нагрузку в численном эксперименте принималась нагрузка, передаваемая через грузораспределительные пластины, при которой в арматуре нарастали пластические деформации, наклонная трещина имела чрезмерное «раскрытие» (зона элементов с «заниженным» значением модуля деформации разрасталась на 3 и более элементов по ширине трещины), после данных шагов приближения нелинейная задача, как правило, переставала сходиться. Сравнение значений разрушающей нагрузки приведено в табл. 2.
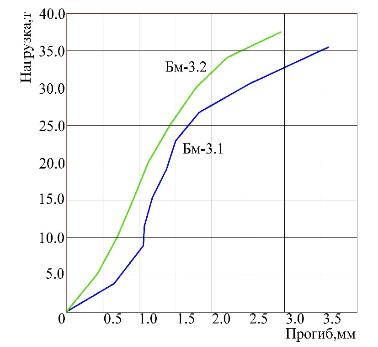
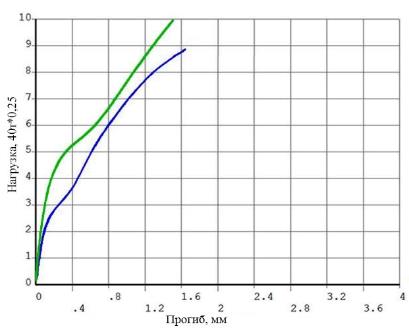
Рис. 7. Графики «прогиб - нагрузка», полученные в ходе: а) натурного эксперимента; б) численного эксперимента.
Таблица 2
Разрушающая нагрузка, определенная различными методами
|
|
СП 63.13330.2012 [5] |
Ansys |
ACI 440.2R-08 [7] |
Fib Bulletin 14 [10] |
|
Бм-1.1 (без Qsw) |
15,8 |
17,0 |
- |
- |
|
Бм-2.1 (110) |
22,1 |
31,0 |
- |
- |
|
Бм-3.1 (85) |
23,9 |
33,0 |
- |
- |
|
Бм-1.2 (без Qsw)+ФАП |
- |
"+"15,7 |
"+"2,7 |
"+"2,9 |
|
Бм-2.2 (110)+ФАП |
- |
"+"3,9 |
"+"2,7 |
"+"2,9 |
|
Бм-3.2 (85)+ФАП |
- |
"+"2,8 |
"+"2,7 |
"+"2,9 |
|
Бм-1.3 (без Qsw)+ФАП α |
|
"+"22,7 |
"+"3,8 |
"+"4,1 |
|
Бм-2.3 (110)+ФАП α |
|
"+"7,2 |
"+"3,8 |
"+"4,1 |
|
Бм-3.3 (85)+ФАП α |
|
"+"5,1 |
"+"3,8 |
"+"4,1 |
* "+" означает прирост прочности по наклонному сечению по сравнению с неусиленным образцом.
Рецензенты:
Пухаренко Ю.В., д.т.н., профессор, зав. кафедрой «Строительные материалы и технологии» ФГБОУ ВПО «Санкт-Петербургский государственный архитектурно-строительный университет», г. Санкт-Петербург.
Егоров В.В., д.т.н., профессор, зав. кафедрой «Строительные конструкции» ФГБОУ ВПО «Петербургский государственный университет путей сообщения им. императора Александра I», г. Санкт-Петербург.



