Уже длительное время моделирование различных процессов и явлений имеет необычайно широкое применение во многих областях знаний. моделирование – главный способ познания окружающего мира.
С процессом моделирования и различными моделями мы сталкиваемся с раннего детства. В школе практически все обучение построено на использовании моделей в той или иной форме: от структурных схем, таблиц и т.п. до различных макетов.
В этой связи возникает необходимость широкого внедрения метода математического моделирования как в учебные программы базового курса математики вузов, так и в программы элективных и факультативных курсов в средней школе.
Согласно Н.А. Терёшину [5], можно выделить 3 основные функции математического моделирования.
-
Познавательная функция отвечает за формирование познавательного образа исследуемого объекта, которое происходит постоянно при переходе от простого к сложному.
-
Функция управления деятельностью обучаемых. Поскольку математическое моделирование носит предметный характер, оно призвано облегчить контрольные, ориентировочные и коммуникационные действия.
-
Интерпретационная функция. Суть этой функции в том, что один и тот же объект может быть выражен с помощью разных моделей. Например, окружность может быть задана посредством уравнений относительно осей координат, пары объектов (центр и радиус), а также рисунка или чертежа, т.е. можно воспользоваться либо аналитическим выражением, либо геометрической моделью.
Помимо указанных функций, в литературе можно встретить и такие функции моделирования, как эстетическая, функция обеспечения целенаправленного внимания учащихся, запоминания и повторения учащимися учебного материала и др.
Еще одной, не менее важной, является эвристическая функция математической модели. Математическая модель позволяет экспериментировать с количественной стороной объекта, еще глубже проникнуть в качественный аспект объекта – показать его внутренние закономерности, дает возможность определить границы устойчивости, нормальный и оптимальный режимы функционирования.
Использование разнообразных функций математической модели развивает мышление студентов, так как их внимание своевременно и легко переключается с рассматриваемой модели на информацию о данном объекте, которая получена с ее помощью и обратно. Подобное переключение обеспечивает отвлечение умственных усилий студентов от предмета их деятельности.
Для современного развития общества характерны интеграционные процессы, которые проявляются в стремлении наиболее точно представить общую картину мира.
Термин «интеграция» (от лат. integer – целый) означает создание неразрывно связанного, единого, целого. Общенаучное понятие теории систем – интеграция – это состояние связанности отдельных частей в целое, а также процесс, ведущий к такому состоянию, к восстановлению какого-либо единства.
Все чаще в теории и практике обучения прослеживается тенденция к интеграции учебных дисциплин. Реализация интегрированного обучения позволяет достигать межпредметных обобщений и приближаться к пониманию общей картины мира. Интеграция как средство обучения дает знания, демонстрирующие связанность отдельных предметов и областей знания, научить обучающихся с первых шагов воспринимать мир как единое целое, в котором все элементы взаимосвязаны.
В условиях всевозрастающего и постоянно меняющегося объема информации, в том числе учебной при постоянных сроках обучения, интеграция математики с профильными дисциплинами становится все более актуальной. Она позволяет сократить количество изучаемых дисциплин, объем учебной информации, время изучения учебного материала, ликвидировать дублирование, расширить представление об изучаемом объекте, изменить стиль мышления обучаемых.
Чтобы построить математическую модель и работать с ней, необходимо овладеть следующими умениями.
Формализация – построение модели объекта или явления, т.е. перевод конкретной задачи с естественного языка на математический язык формул, уравнений, неравенств, систем.
Работа с моделью – оперирование формальными структурами, структурными соотношениями и их связями. Конкретно это выражается в выборе алгоритма для решения уравнений и неравенств, построении графиков и т. п.
Владение компьютерными технологиями – это создание программ, «переводящих» модель и алгоритм на доступный компьютеру язык. Их можно назвать «электронным» эквивалентом изучаемого объекта, пригодным для непосредственного испытания на «экспериментальной установке» – компьютере.
Интерпретация – перевод результатов с математического языка на язык исходной задачи, описание области применения полученных результатов.
Все эти мыслительные процессы составляют процесс математического моделирования.
Таким образом, введение математического моделирования в качестве компонента математической подготовки обеспечивает формирование научного мировоззрения, прикладную и профильную направленность математической подготовки, системность знаний обучаемых, развитие их мыслительных операций, таких как анализ, сравнение, обобщение, конкретизация и т.п., необходимых в современных условиях.
Необходимость формирования навыков математического моделирования при обучении математике обосновывается в работах Е.Ы. Бидайбекова, В.В. Давыдова, О.Б. Епишевой, O.A. Ивашовой, В.И. Крупича, А.Г. Мордковича, Н.И.Пака, Г.И. Саранцева, Ю.Г. Тамберга, T.M. Фридмана и др. Авторы утверждают, что навыки моделирования должны приобретаться учащимися еще со школьной скамьи. Но практически этот подход остается нереализованным. Пожалуй, замечательное исключение составляют школьные учебники по математике под редакцией А.Г. Мордковича [1].
В связи с этим для обеспечения непрерывности обучения методу математического моделирования учащихся и студентов естественнонаучного профиля разработано учебное пособие «Математическое моделирование химических процессов» [4].
Пособие состоит из трех частей, непрерывно следующих друг за другом, и предполагает три этапа обучения.
Первая глава – «Теоретические основы математического моделирования» – содержит справочник по элементарной математике, необходимой при решении химических задач [2]. Дан анализ большого количества примеров решения химических задач средствами математики. Решения некоторых задач представлены двумя способами – химическим и математическим. В конце каждой темы предлагаются задачи (как химические, так и из курса элементарной математики) для самостоятельного решения, что позволяет отрабатывать полученные знания, умения и навыки, а также творческие задания для выполнения с использованием метода проектов.

Рис.1. Решение задач по химии двумя способами
Данная часть пособия нацелена на обучение математике учащихся 9-х классов. Основная цель первого этапа обучения – создание ориентационной и мотивационной основы для осознанного выбора естественнонаучного профиля дальнейшего.
Вторая глава ориентирована на учащихся 10–11-х классов (второй этап обучения), выбравших естественнонаучный профиль. В ней освещена роль математики в химии, даны теоретические основы метода математического моделирования (определения, законы построения математических моделей, основные этапы математического моделирования), классификация моделей по различным критериям [3].
Здесь же представлены модели, описываемые линейными уравнениями и неравенствами, системами уравнений, графические математические модели. Большое значение имеет здесь описанное большое количество примеров построения математических моделей на основе расчетных задач школьной химии и задачи на самостоятельное составление математических моделей (рис. 2).

Рис. 2. Описание процесса построения математической модели
Так как вторая глава пособия является логическим продолжением первой, то решение построенных моделей не вызывает трудности у школьников, поскольку большинство задач для построения математических моделей взято из изученного уже курса.
На третьем этапе (изучение третьей главы пособия) студентам даются основы проведения параметрического анализа математических моделей (рис. 3). Здесь необходимы знания по таким разделам математики, как дифференциальное и интегральное исчисления, дифференциальные уравнения, линейная алгебра.
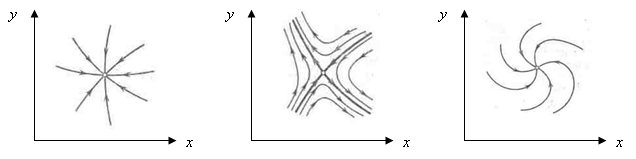
Рис.3. Исследование типа стационарных состояний:
а) устойчивый узел; б) седло; в) устойчивый фокус
Таким образом, курс «Математическое моделирование химических процессов» на качественном уровне знакомит учащихся и студентов с наиболее важными проблемами естественных наук и на количественном уровне знакомит их с методами построения математических моделей важнейших современных концепций, то есть является средством формирования методологии научного познания. Он позволяет закрепить практические навыки, приобретенные при изучении математики, информатики, а также специальных дисциплин и способствует освоению логики процесса научного исследования, пониманию особенностей теоретического этапа и разных уровней исследования в естественных науках.
Рецензенты:
Пак Н.И., д.п.н., профессор, зав. базовой кафедрой информатики и информационных технологий в образовании, ФГБОУ ВПО «КГПУ им. В.П. Астафьева», г. Красноярск;
Добронец Б.С., д.ф.-м..н., профессор, зав. кафедрой информационных систем, ФГАОУ ВПО «СФУ», г. Красноярск.



